Définition de l'intégrale

La « définition » ci-dessous, bien que prescrite par les programmes, n'est qu'« intuitive » car basée sur la notion d'aire, dont la définition mathématique dépasse largement le niveau de ce cours. Il faut donc se contenter de l'intuition de cette notion, issue de la « connaissance » de l'aire des figures planes usuelles.

Définition

Soit ${\displaystyle f}$ une fonction continue et positive sur un intervalle ${\displaystyle [a,b]}$ (${\displaystyle a\leq b}$) et soit ${\displaystyle {\mathcal {C}}}$ la courbe représentative de ${\displaystyle f}$ sur ${\displaystyle [a,b]}$.

On considère la portion du plan délimitée par :

${\displaystyle \left\{{\begin{array}{l}x=a{\text{$ : droite verticale}}\\x=b{\text{ : droite verticale}}\\y=0{\text{ : axe des abscisses}}\\C:y=f(x){\text{ : courbe de }}f\\\end{array}}\right.}

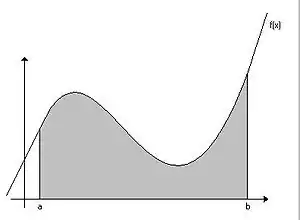
alors l'aire de cette figure est appelée l'intégrale de ${\displaystyle f}$ de ${\displaystyle a}$ à ${\displaystyle b}$ et notée :

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$

ou plus simplement :

${\displaystyle \int _{a}^{b}f}$.

On étend ensuite cette définition :

• à une fonction ${\displaystyle f}$ continue mais non nécessairement positive, en exprimant ${\displaystyle f}$ comme différence de deux fonctions continues positives, ${\displaystyle f=f_{+}-f_{-}}$, et en définissant l'intégrale de ${\displaystyle f}$ comme la différence des intégrales de ces deux fonctions ;
• à l'intégrale de ${\displaystyle b}$ à ${\displaystyle a}$ (avec encore ${\displaystyle b\geq a}$), définie comme l'opposée de l'intégrale de ${\displaystyle a}$ à ${\displaystyle b}$.

Remarques

• ${\displaystyle \int _{a}^{a}f=0}$.
• Dans l'écriture traditionnelle, ${\displaystyle x}$ est une variable « muette », c'est-à-dire que la lettre choisie est arbitraire, mais ne doit surtout pas être une lettre déjà utilisée par ailleurs (comme ici ${\displaystyle a}$ ou ${\displaystyle b}$) : ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\int _{a}^{b}f(q)\,\mathrm {d} q}$.
• De même que dans l'expression d'une limite, il n'est pas vraiment indispensable de l’écrire, si on l'omet également dans l'expression de la fonction à intégrer : ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x=\int _{a}^{b}f}$. Mais cette écriture simplifiée n'est possible que si la fonction à intégrer est désignée par une lettre (ici ${\displaystyle f}$) et non par une formule.

Lien entre intégrale et primitive

Théorème fondamental de l'analyse

Soient ${\displaystyle f}$ une fonction continue sur un intervalle ${\displaystyle I}$ et ${\displaystyle a}$ un élément de ${\displaystyle I}$.

L'application ${\displaystyle x\mapsto \int _{a}^{x}f}$ est une primitive de ${\displaystyle f}$ sur ${\displaystyle I}$.

À notre niveau, ce théorème ne peut pas être démontré et n'a même pas de signification précise, puisqu'en définitive, l'intégrale n'a pas été définie mathématiquement. On pourrait, à rebours, le prendre comme une définition de l'intégrale d'une fonction continue, en admettant qu'une telle fonction a des primitives.

Notation crochet

Soit ${\displaystyle F}$ une fonction.

On note ${\displaystyle [F(x)]_{x=a}^{x=b}}$, ou plus simplement ${\displaystyle [F]_{a}^{b}}$ le réel ${\displaystyle F(b)-F(a)}$.

Corollaire

Toute fonction ${\displaystyle f}$ continue sur un intervalle admet des primitives, et si ${\displaystyle F}$ est l'une d'elles, on a (pour tous ${\displaystyle a}$ et ${\displaystyle b}$ dans cet intervalle) :

${\displaystyle \int _{a}^{b}f=[F]_{a}^{b}}$.

Remarque

L'intégrale ne dépend pas de la primitive choisie. En effet, si ${\displaystyle G=F+k}$ est une autre primitive de ${\displaystyle f}$ :

${\displaystyle [G]_{a}^{b}=[F+k]_{a}^{b}=[F]_{a}^{b}+[k]_{a}^{b}=[F]_{a}^{b}}$.

Exemple

Calculer le réel ${\displaystyle I:=\int _{0}^{1}{(x-x^{2}+1)}~\mathrm {d} x}$ qui, par définition, représente l'aire ci-dessous :

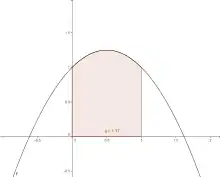
On note : ${\displaystyle f:x\mapsto \cdots }$.

Donc une primitive de ${\displaystyle f}$ est : ${\displaystyle F:x\mapsto \cdots }$.

Et ${\displaystyle I=\int _{0}^{1}{(x-x^{2}+1)}~\mathrm {d} x=\cdots }$.