Remarque : Pour une compréhension intuitive de la notion de limite, voyez les premiers chapitres du cours Limites d'une fonction.
Soient une partie de , une fonction de dans , et un point adhérent à .
- Les deux cas les plus fréquents de cette notion de topologie générale sont un intervalle réel ou (pour une suite) ; il suffit, pour ces deux cas, de savoir que :
- aucun point n'est adhérent à ;
- si est un intervalle non vide d'extrémités , l'ensemble des points de adhérents à est ;
- l'ensemble des points de adhérents à est .
Définitions formalisées
Limite finie en un point
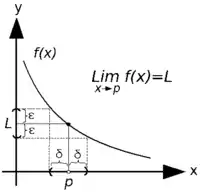
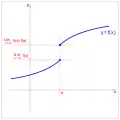
Si , a pour limite en le réel si :
En français, on pourrait dire que a pour limite en si, pour un intervalle choisi autour de aussi petit que l’on veut, il existe un intervalle de valeurs de autour de pour lequel tous les appartiennent à .
On note alors ou, de manière plus condensée, .
Ici et dans la suite de cette leçon, on a fait le choix d'une inégalité stricte pour l'« écart de confiance » (ici : ) et d'une inégalité large pour l'« écart de tolérance » (ici : ), mais on obtiendrait des définitions équivalentes en faisant, pour l'un ou l'autre, le choix inverse. Par exemple ici (avec, pour alléger, ) :
- si alors (en choisissant pour un associé, dans l'hypothèse, à n'importe quel strictement inférieur à , par exemple ) ;
- si alors (en prenant un associé, dans l'hypothèse, à , puis en choisissant pour n'importe quel réel strictement compris entre et , par exemple ) ;
- on peut combiner ces deux techniques pour les autres variantes.
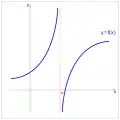
Limite infinie en un point
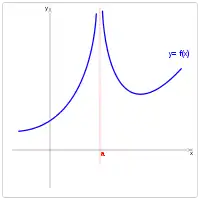
Si , a pour limite en :
- si :;
- si :.
En français, cela revient à dire que, aussi grand (ou petit) qu'on prenne un réel , en se rapprochant suffisamment de , on finit par dépasser la valeur de . prend ainsi des valeurs infiniment grandes (ou petites) au voisinage de .
On note :
- ou si a pour limite en
- ou si a pour limite en
Limite finie en l'infini
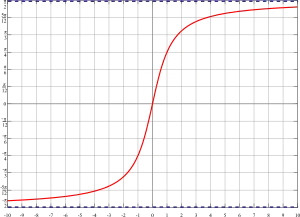
a pour limite le réel :
- en (supposé adhérent à ) si :.
- en (supposé adhérent à ) si :.
En français, tout intervalle ouvert contenant contient aussi toutes les valeurs pour suffisamment :
- grand si a pour limite en . On note alors ou ;
- petit si a pour limite en . On note alors ou .
Limite infinie en l'infini
a pour limite :
- en (supposé adhérent à ) si :;
- en (supposé adhérent à ) si :.
En français, cela revient à dire que tout intervalle contient toutes les valeurs de pour suffisamment :
- grand si a pour limite en . On note alors ou ;
- petit si a pour limite en . On note alors ou .
a pour limite :
- en (supposé adhérent à ) si :;
- en (supposé adhérent à ) si :.
En français, cela revient à dire que tout intervalle contient toutes les valeurs de pour suffisamment :
- grand si a pour limite en . On note alors ou ;
- petit si a pour limite en . On note alors ou .
Limite « épointée » en un point
Si est adhérent à , la limite épointée de en est, si elle existe, la limite (finie ou infinie) en de la restriction de à .
On la note alors .
On a donc :
- si , ;
- si , .
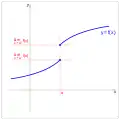
Limite « unilatérale » en un point
Si est adhérent à , la limite à gauche de en est, si elle existe, la limite (finie ou infinie) en de la restriction de à .
On définit de même la limite à droite en remplaçant par .
On note (lorsqu'elles existent) :
- ou ou la limite à gauche ;
- ou ou la limite à droite.
Théorèmes sur les limites
Premières propriétés
Si , alors cette limite est unique.
C'est une conséquence immédiate de la propriété ci-dessous « Limites et relation d'ordre », appliquée à .
On va maintenant voir comment caractériser une limite de fonction à partir de limite de suite.
si, et seulement si :
|
Pour toute suite à valeurs dans qui converge vers , la suite tend vers . |
- Réciproquement, supposons que l’on n'a pas et montrons qu’il existe une suite de réels qui converge vers , et telle que la suite ne converge pas vers . On ne donne ici la preuve que pour une limite finie en un point, mais elle est transposable aux autres cas. Par négation de , il existe un tel que
donc tel que
ce qui conclut.
Limites et opérations
Soient et deux fonctions définies sur un intervalle à valeurs dans , et .
Si et , alors :
- ;
- ;
- si , alors est bien définie au voisinage de et , en particulier .
Par hypothèse, pour tout , il existe tels que pour tout :
- ;
- ;
donc en posant :
- .
Fixons . On a :
- Pour la somme :
- D'après l'inégalité triangulaire, si et alors
- .
- En choisissant on a donc :
- si alors ,
- ce qui prouve que .
- Pour le produit : si et alors
- .
- En choisissant on a donc :
- si alors ,
- ce qui prouve que .
- Pour la combinaison linéaire :
- La propriété se déduit de celles pour le produit (par la fonction constante ) et la somme.
- Pour l'inverse :
- Si alors et
- .
- En choisissant on a donc :
- si alors et ,
- ce qui prouve que est bien définie au voisinage de et .
- Pour le quotient :
- La propriété se déduit de celles pour le produit et l'inverse.
Ces propriétés sont aussi valables (et se démontrent de la même façon) pour les limites à droite et à gauche, pour le cas p = ±∞, et aussi pour les limites infinies en utilisant les règles suivantes :
- q + ∞ = ∞ pour q ≠ -∞
- q × ∞ = ∞ si q > 0
- q × ∞ = -∞ si q < 0
- q / ∞ = 0 si q ≠ ± ∞.
Remarquons qu’il n'y a pas de règle générale pour le cas q/0 : cela dépend de la façon dont on s'approche de 0. Certains cas, comme 0/0, 0 × ∞, ∞-∞ ou ∞/∞, ne sont pas non plus couverts par ces règles.
Formes indéterminées
Il existe certaines formes de limite où il est n’est pas possible de conclure directement en utilisant des opérations sur les limites, ce sont les formes indéterminées (FI) :
- Indétermination de la forme 0/0 quand le résultat obtenu donne 0/0
- Indétermination de la forme ∞/∞ quand le résultat obtenu donne ∞/∞
- Indétermination de la forme ∞ - ∞ quand le résultat obtenu donne ∞ - ∞
- Indétermination de la forme 0 × ∞ qui se ramène aux deux premiers cas en remarquant qu'une multiplication par 0 équivaut à une division par l'infini, ou qu'une multiplication par l'infini équivaut à une division par 0.
Règles opératoires pour lever l'indétermination :
Voici quelques règles opératoires pour lever les FI :
- Fonctions polynomiales et rationnelles :
On a la règle "des monômes de plus haut degré" qui n'est valable qu'en l'infini:
- La limite en l'infini d'une fonction polynomiale est égale à celle de son monôme (ou terme) de plus haut degré.
- La limite en l'infini d'une fonction rationnelle est égale à celle du quotient de ses monômes de plus hauts degrés.
(démonstration à faire)
Exemples :
1/ Soit .Le monôme de plus haut degré est .
Alors
et de même : .
2/ Soit .Les monômes de plus hauts degrés sont et .
Alors .
- Factorisation par le terme "le plus fort en l'infini" :
(à faire) - Règle de L'Hospital :
Du nom du marquis de L'Hospital, mathématicien français du XVIIe siècle, cette règle permet de simplifier les FI 0/0 ou ∞/∞ : voir Fonctions d'une variable réelle/Dérivabilité).
Limite d'une fonction composée
Soient et deux parties de , et deux applications, et , avec adhérent à .
On pourrait formuler cette démonstration en termes généraux de voisinages, mais traitons plus explicitement deux cas (dans tous les autres cas, la démonstration est identique après modification de la forme des voisinages).
- Premier cas : .
- Soit .
- Comme , il existe tel que .
- Puis, comme , il existe tel que .
- On a donc bien associé à chaque un tel que
, d'où le résultat.
- Deuxième cas : .
- Soit .
Comme , il existe tel que . - Puis, comme , il existe tel que .
- On a donc bien associé à chaque un tel que
, d'où le résultat.
- Soit .
Calculer .
Par définition, pour tout :
- où et .
Or :
- ;
- donc (première application de la propriété) ;
donc en appliquant une deuxième fois la propriété :
|
. |
Limites et relation d'ordre
Les trois théorèmes qui suivent sont valables mutatis mutandis pour . Ils se généralisent même à des fonctions définies sur une partie d'un espace topologique quelconque , avec adhérent à .
Soient et définies sur et un réel adhérent à en lequel et admettent chacune une limite (finie ou infinie).
Soit un réel strictement compris entre et . Par définition des limites (qu'elles soient finies ou infinies) :
- ;
- .
En prenant , on en déduit le résultat annoncé.
Par exemple (pour ou constante) :
- si alors ;
- si alors .
En affaiblissant la contraposée du théorème, on en déduit la propriété de passage à la limite dans les inégalités :
Sous les mêmes hypothèses,
Par exemple (pour ou constante, et en remplaçant par ) :
- si alors ;
- si alors .
Attention ! Ce corollaire devient faux si l'on remplace les inégalités larges par des inégalités strictes.
Contre-exemple : est à valeurs strictement positives sur , mais .
Les deux théorèmes suivants sont très utiles dans la pratique :
Soient , et trois fonctions définies sur , et un réel adhérent à .
Si et , alors .

Dans les applications de ce théorème et du suivant, si les inégalités entre fonctions ne sont réalisées que sur une partie de , on peut toujours restreindre les fonctions à ce domaine plus petit, pourvu que y soit encore adhérent.
Exemple. En appliquant le théorème à
- , encadrée sur par
- et (car ),
on trouve, puisque et :
- Puisque , il existe tel que
- .
- Puisque , il existe tel que
- .
Posons . D'après la propriété d'encadrement, on obtient :
- .
On a donc bien associé, à tout intervalle ouvert contenant , un tel que
- ,
Soient , et trois fonctions définies sur , et un réel adhérent à .
- Si et , alors .
- Si et , alors .
Exemple : Soit .
Comme et comme , on en déduit que .
Soit . Puisque , il existe tel que
- .
Puisque , on obtient alors :
- ,
Théorème de la limite monotone
On utilise la convention suivante, pour une partie non vide de :
- si est non majorée, alors ;
- si est non minorée, alors .
Soient une partie de , une application croissante et adhérent à (resp. ). Alors,
On a des résultats analogues pour décroissante, en intervertissant et .
Cf. Ramis, Deschamps et Odoux, Cours de mathématiques spéciales, vol. 3, Masson, 1976, p. 119-120.
Notons et (qui, de même que , peut être fini ou ).
Soit . Par définition de , le réel n'est pas un majorant de . Il existe donc un réel tel que . Par croissance de , on obtient ainsi :
D'autre part, tous les vérifient : . On a donc démontré :
En particulier, une application monotone bornée sur un intervalle possède une limite finie à gauche et une limite finie à droite en tout point de cet intervalle, ainsi qu'une limite à droite en et une limite à gauche en .