Définition et interprétation géométrique
Soit une fonction définie sur un intervalle et .
La fonction est dite :
- continue en si ;
- continue sur si elle est continue en tout réel de .
Interprétation géométrique « naïve »:
Une fonction continue est une fonction dont on peut tracer le graphe sans lever le crayon.
Exemples et contre-exemples :
- La fonction est continue sur .
- La fonction est continue sur mais pas en 0 (tout simplement parce qu'elle n'y est pas définie !).
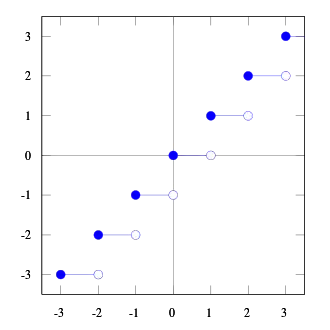
- La fonction partie entière n'est continue en aucun point de .
- On rappelle que cette fonction est définie par :.Elle a un graphique « en escalier » (voir illustration ci-contre) : par exemple, mais .
- On rappelle que cette fonction est définie par :
Remarque : Cette interprétation fonctionne bien dans la très grande majorité des cas, mais il existe des cas « pathologiques ». Par exemple, la fonction définie par
n'est continue qu'en zéro (du fait de la densité de dans , on ne peut tracer la courbe de ).
Prolongement par continuité
Soient un intervalle de , et une fonction continue sur .
Si , le prolongement par continuité de en est la fonction définie sur par :
Exemple : On connaît la limite . Si la fonction est définie par , son prolongement par continuité en est donc :
Continuité et opérations
Les propriétés suivantes découlent directement des propriétés correspondantes pour les limites de fonctions (limites et opérations et limite d'une fonction composée).
- Soient et deux fonctions continues en (respectivement sur un intervalle ) et soit . Alors :
- est continue en (resp. sur ) ;
- est continue en (resp. sur ) ;
- si de plus , alors est continue en (resp. sur ).
- Soient continue en et continue en (resp. continue sur et continue sur ), alors est continue en (resp. sur ).
Théorèmes sur les fonctions continues
Voici trois théorèmes importants sur les fonctions continues réelles (ils possèdent des généralisations en topologie).
Soit une fonction continue sur un intervalle .
Pour tout réel compris entre et , l'équation admet au moins une solution sur .
Ainsi, le segment d'extrémités est inclus dans .
En résumé :
|
L'image par une fonction continue d'un intervalle est un intervalle. |
Supposons par exemple f(a) ≤ u ≤ f(b), et notons X le sous-ensemble de l'intervalle [a, b] constitué des réels x qui vérifient f(x) ≤ u.
Cet ensemble est non vide (il contient a) et majoré (par b).
Notons c sa borne supérieure et prouvons que f(c) = u.
- Comme , on a (par passage à la limite dans les inégalités) f(c) ≤ u.
- Reste à prouver que f(c) ≥ u.
- Si c = b, c'est vrai par hypothèse.
- Si au contraire l'intervalle ]c, b] est non vide, comme ses éléments x vérifient tous f(x) > u, on obtient (à nouveau par passage à la limite) f(c) ≥ u.
- Cette inégalité et la précédente prouvent l'égalité voulue.
Pour une autre preuve (par dichotomie), voir Continuité et variations/Théorème des valeurs intermédiaires.
Toute fonction continue sur un intervalle fermé borné (non vide) est bornée et y atteint ses bornes. Autrement dit : Soit une fonction continue sur un intervalle , alors il existe tels que et , ou encore, en tenant compte du théorème précédent, tels que :
En résumé :
|
L'image par une fonction continue d'un intervalle fermé borné est un intervalle fermé borné. |
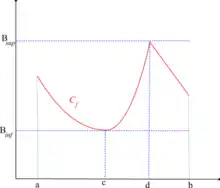
Notons la borne supérieure de l'ensemble , au sens large a priori, c'est-à-dire égale à si n'est pas majorée, et prouvons qu'elle est atteinte (donc en fait finie).
Pour tout réel , posons
- (inclus dans et non vide) et .
Comme , on a (par passage à la limite dans les inégalités)
- .
Par ailleurs, comme la fonction est décroissante, quand , (théorème de la limite monotone) et par continuité :
- .
À nouveau par passage à la limite, on déduit de ces deux points que , donc :
- .
Le résultat pour la borne inférieure s'en déduit en remplaçant par , ou se démontre de même.
Il existe bien d'autres démonstrations du théorème des bornes. Voir par exemple Spivak, Calculus, p. 115-116.
Soit une fonction continue et strictement croissante (resp. décroissante), et l'intervalle (resp. ). Alors :
- réalise une bijection de sur ;
- la bijection réciproque, de sur — strictement croissante (resp. décroissante) —, est continue.
On dit aussi que réalise un homéomorphisme entre et . Le point essentiel de ce théorème est la continuité de la réciproque. Elle repose sur le lemme suivant, dont l'énoncé est rarement explicité mais figure dans Alain Mézard et Charles Delorme, Cours de mathématiques supérieures, vol. 2, PUF, 1994, p. 101 et 255.
|
Lemme — Toute surjection monotone d'une partie de sur un intervalle est continue. |
- Preuve du lemme
- Soient une partie de , un intervalle de , une surjection croissante (si est décroissante, considérer ) et non constante (car ce cas est immédiat), et .
- S'il existe tel que alors, pour tout , en posant puis et , on obtient : et .
- Si , on trouve de même, pour tout , un tel que .
- Si , on trouve de même, pour tout , un tel que .
- Dans les trois cas, on a démontré que est continue en .
- Preuve du théorème
- On suppose que est strictement croissante (si est décroissante, considérer ).
- est strictement croissante donc injective. C'est donc une bijection de dans .
- D'après le théorème des valeurs intermédiaires, est un intervalle.
- Par monotonie, .
- La bijection réciproque, de sur , est (strictement) croissante, donc continue d'après le lemme.
D'après le lemme, toute bijection monotone entre intervalles réels est continue. La réciproque se généralise :
On peut utiliser des arguments de connexité, ou démontrer plus généralement que toute fonction de Darboux (c'est-à-dire toute fonction vérifiant la propriété des valeurs intermédiaires) injective sur un intervalle [a, b] est monotone : soit f une telle fonction, avec par exemple f(a) < f(b). Pour tous x < y dans [a, b[, par hypothèse sur f, f(a) et f(x) sont d'un côté de f(y) et f(b) est de l'autre côté, donc f(x) < f(y) < f(b) et f est croissante.