Équations et fonctions du second degré/Fonctions polynômes du second degré (ou trinômes)

Les fonctions trinôme

Définition

Une fonction polynomiale du second degré, ou fonction trinôme, est une fonction qui peut s'exprimer sous la forme : $f:x\mapsto ax^{2}+bx+c$

avec

a, b et c trois coefficients réels
a non nul.

On parle de second degré car la puissance de x la plus élevée est 2.

Pour l'étude générale des fonctions polynomiales du second degré, il est très important de prendre a non nul, sinon on n'aurait plus une fonction du second, mais du premier degré maximum.

Exemple

f(x) = 4x² − 5x est une fonction polynôme du second degré avec a = 4, b = −5 et c = 0.
g(x) = (2x + 1)² − (2x − 3)² = 4x² + 4x + 1 − (4x² − 12x + 9) = 16x − 8 n'est pas une fonction polynôme du second degré parce que a = 0.

De la définition précédente, on déduit qu'une fonction trinôme est définie sur $\mathbb {R}$ tout entier.

Être ou ne pas être une fonction trinôme

Point ajouté pour une réponse juste :
Point retiré pour une réponse incorrecte :
Ignorer les coefficients des questions :

	$f_{1}:x\mapsto 2x^{2}+3x+1$
	$f_{2}:x\mapsto x^{2}-2x+2$
	$f_{3}:x\mapsto 2x+1$
	$f_{4}:x\mapsto -x^{3}+2x-5$
	$f_{5}:x\mapsto x^{2}+3$
	$f_{6}:x\mapsto 3x^{2}-x$

f_{1}:x\mapsto -2x^{2}+3x-5

a=

b=

c=

f_{2}:x\mapsto x^{2}-5x+1

a=

b=

c=

f_{3}:x\mapsto 3x+10x^{2}-7

a=

b=

c=

Écriture des fonctions polynomiales

Il est d’usage d'écrire les fonctions polynomiales par termes de degrés décroissants :

$3x^{4}+6x^{9}-2$ est mal écrit car le terme de degré 9 est écrit après le terme de degré 4
$-7x^{4}+8x-\pi$ est correctement écrit.

Variations d'une fonction trinôme

Définition

La forme canonique d'un trinôme du second degré

f(x)=ax^{2}+bx+c

est son expression sous la forme

f(x)=a(x-\alpha )^{2}+\beta

où

\alpha =-{\frac {b}{2a}}\quad {\text{et}}\quad \beta =-{\frac {b^{2}-4ac}{4a}}

.

Démonstration

Par identification des coefficients, le polynôme $a(x-\alpha )^{2}+\beta =ax^{2}+(-2\alpha a)x+(a\alpha ^{2}+\beta )$ est égal à $ax^{2}+bx+c$ si et seulement si

-2\alpha a=b

et

a\alpha ^{2}+\beta =c

, c'est-à-dire

\alpha =-{\frac {b}{2a}}

et

\beta =c-a\left(-{\frac {b}{2a}}\right)^{2}

,

et l'on a bien

c-a\left(-{\frac {b}{2a}}\right)^{2}={\frac {4ac}{4a}}-{\frac {b^{2}}{4a}}=-{\frac {b^{2}-4ac}{4a}}

.

On retrouvera cette forme canonique au chapitre suivant

Théorème

Les variations de la fonction du second degré définie sur $\mathbb {R}$ par sa forme canonique :

f(x)=a(x-\alpha )^{2}+\beta

sont données par les tableaux suivants.

{\begin{array}{c|ccccc||ccccc}&{\text{Si }}a>0&&&&&{\text{Si }}a<0&&&&\\\hline x&-\infty &&\alpha &&+\infty &-\infty &&\alpha &&+\infty \\\hline &+\infty &&&&+\infty &&&\beta &&\\{\text{Variations de }}f&&\searrow &&\nearrow &&&\nearrow &&\searrow &\\&&&\beta &&&-\infty &&&&-\infty \\\end{array}}

Exemple

Étudier le sens de variation de la fonction f définie sur R par f(x) = 2x² − 5x + 1.
Dresser le tableau des variations de f sur [0, 3].

Solution

f est une fonction du second degré sous la forme ax² + bx + c avec a = 2, b = −5 et c = 1.

a > 0 donc la courbe représentée de f est une parabole de sommet S(x_S ; y_S) « tournée vers le haut »

On a :

x_{S}={\frac {-b}{2a}}={\frac {-(-5)}{2\times 2}}={\frac {5}{4}}

Donc f est décroissante sur ]−∞, ${\tfrac {5}{4}}$ ] et croissante sur [ ${\tfrac {5}{4}}$ , +∞[.

On calcule donc :

$f(0)=2\times 0^{2}-5\times 0+1=1$ ;
$f(3)=2\times 3^{2}-5\times 3+1=18-15+1=4$ ;
$f({\tfrac {5}{4}})=2\times ({\tfrac {5}{4}})^{2}-5\times {\tfrac {5}{4}}+1={\frac {25}{8}}-{\frac {25}{4}}+1={\frac {25}{8}}-{\frac {50}{8}}+{\frac {8}{8}}={\frac {-17}{8}}$ .

D'après la question précédente, on a donc :

${\begin{array}{c|ccccc|}x&0&&-{\tfrac {5}{4}}&&3\\\hline &1&&&&4\\{\text{Variations de }}f&&\searrow &&\nearrow &\\&&&{\tfrac {-17}{8}}&&\\\end{array}}$

Complément : dérivée

Cette section nécessite des connaissances sur les dérivées, de niveau 12. Si vous n'êtes pas de ce niveau, vous pouvez passer directement à la section suivante. Si vous le souhaitez, vous pouvez consulter les cours de la Wikiversité à ce sujet.

Pour trouver le tableau de variation d'une fonction trinôme, il suffit de la dériver. Soit le trinôme $f:x\mapsto ax^{2}+bx+c$ où $a\neq 0$ .

Pour tout $x\in \mathbb {R} ,~f'(x)=2ax+b$ .

La dérivée de $f$ s'annule en $x=-{\frac {b}{2a}}$

Tableau de variations

Théorème

Le tableau de variations dépend du signe de $a$ . L'expression de la dérivée permet de distinguer deux cas : ${\begin{array}{c|ccccc||ccccc}&{\text{Si }}a>0&&&&&{\text{Si }}a<0&&&&\\\hline x&-\infty &&-\displaystyle {\frac {b}{2a}}&&+\infty &-\infty &&-\displaystyle {\frac {b}{2a}}&&+\infty \\\hline &+\infty &&&&+\infty &&&\displaystyle {f\left(-{\frac {b}{2a}}\right)}&&\\{\text{Variations de }}f&&\searrow &&\nearrow &&&\nearrow &&\searrow &\\&&&\displaystyle {f\left(-{\frac {b}{2a}}\right)}&&&-\infty &&&&-\infty \\\end{array}}$

Exemples

Donner les tableaux de variations des fonctions suivantes.

$f_{1}:x\mapsto 2x^{2}+3x+1$ ;
$f_{2}:x\mapsto x^{2}-2x+2$ ;
$f_{3}:x\mapsto -x^{2}+3$ ;
$f_{4}:x\mapsto -3x^{2}-x$ .

Solution

$f_{1}:x\mapsto 2x^{2}+3x+1$

${\begin{array}{c|ccccc|}x&-\infty &&-{\tfrac {3}{4}}&&+\infty \\\hline {\text{Signe de }}f_{1}'(x)&&-&0&+&\\\hline &+\infty &&&&+\infty \\{\text{Variations de }}f_{1}&&\searrow &&\nearrow &\\&&&-{\tfrac {1}{8}}&&\\\hline \end{array}}$

$f_{2}:x\mapsto x^{2}-2x+2$

${\begin{array}{c|ccccc|}x&-\infty &&1&&+\infty \\\hline {\text{Signe de }}f_{2}'(x)&&-&0&+&\\\hline &+\infty &&&&+\infty \\{\text{Variations de }}f_{2}&&\searrow &&\nearrow &\\&&&1&&\\\hline \end{array}}$

$f_{3}:x\mapsto -x^{2}+3$

${\begin{array}{c|ccccc|}x&-\infty &&0&&+\infty \\\hline {\text{Signe de }}f_{3}'(x)&&+&0&-&\\\hline &&&3&&\\{\text{Variations de }}f_{3}&&\nearrow &&\searrow &\\&-\infty &&&&-\infty \\\hline \end{array}}$

$f_{4}:x\mapsto -3x^{2}-x$

${\begin{array}{c|ccccc|}x&-\infty &&-\displaystyle {\tfrac {1}{6}}&&+\infty \\\hline {\text{Signe de }}f_{4}'(x)&&+&0&-&\\\hline &&&\displaystyle {\tfrac {1}{12}}&&\\{\text{Variations de }}f_{4}&&\nearrow &&\searrow &\\&-\infty &&&&-\infty \\\hline \end{array}}$

Représentation graphique d'une fonction trinôme

Allure de la parabole

Voir les exercices sur : Un trinôme issu d'une situation géométrique.

Du tableau de variations trouvé plus haut, on peut déduire la représentation graphique de la fonction trinôme.

Théorème

La représentation graphique d'une fonction trinôme est toujours une parabole.

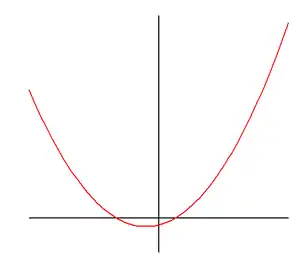
Le sommet est en bas si a est positif (la courbe fait un sourire).
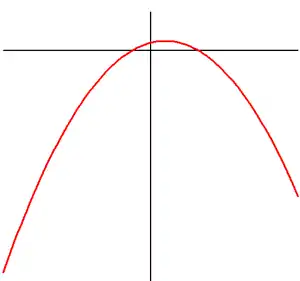
Le sommet est en haut si a est négatif (la courbe fait la moue).

$a>0$	$a<0$

Cette parabole admet un axe de symétrie : la droite d'équation x = x_S.

Sommet

Le point de coordonnées $\left(-{\frac {b}{2a}};-{\frac {b^{2}-4ac}{4a}}\right)$ est le sommet de la parabole.

Si a > 0, alors l'extremum de f est un minimum et le sommet est le point le plus bas de la parabole.
Si a < 0 alors l'extremum de f est un maximum et le sommet est le point le plus haut de la parabole.

Exemple de description

Soit f une fonction polynôme du second degré définie par f(x) = −2x² + 4x + 1.

Décrire la représentation graphique de f.

Solution

f est une fonction du second degré de la forme ax² + bx + c avec a = −2, b = 4 et c = 1.

a < 0 donc sa représentation graphique est une parabole « tournée vers le bas », de sommet S(x_S, y_S) avec :

$x_{S}={\tfrac {-b}{2a}}={\frac {-4}{2\times (-2)}}=1$ ;
$y_{S}=f(x_{S})=f(1)=-2\times 1^{2}+4\times 1+1=3$ .

Exemples de tracés

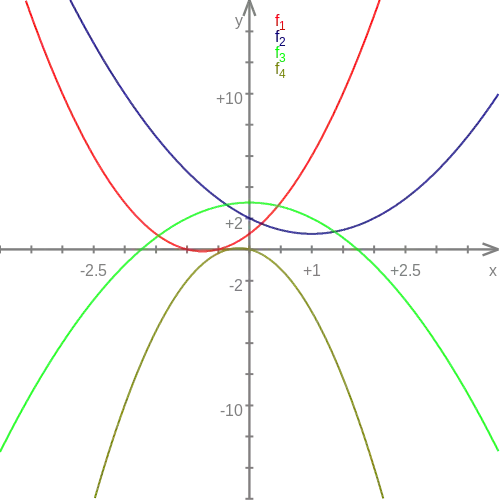
Tracer dans un même repère orthonormé les paraboles représentatives des fonctions suivantes. Vérifier la cohérence avec les tableaux de variations obtenus précédemment.

$f_{1}:x\mapsto 2x^{2}+3x+1$ ;
$f_{2}:x\mapsto x^{2}-2x+2$ ;
$f_{3}:x\mapsto -x^{2}+3$ ;
$f_{4}:x\mapsto -3x^{2}-x$ .

Solution

Liens

Équation du second degré sur Wikipédia, on y trouve les démonstrations des théorèmes de ce cours. Un peu difficile néanmoins.
Fonction du second degré sur Wikipédia, plus élémentaire que le précédent. Une illustration graphique intéressante

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.