Définitions

Racines d'une fonction polynomiale

Les racines d'une fonction trinôme f sont les solutions de l'équation f(x) = 0.

Graphiquement, ce sont les abscisses des points d'intersection de la parabole avec l’axe des abscisses (horizontal).

Discriminant

Soit f une fonction polynomiale définie par ${\displaystyle f:x\mapsto ax^{2}+bx+c}$, avec

• a, b, c trois réels
• a non nul.

Le discriminant de f est le réel ${\displaystyle \Delta =b^{2}-4ac}$.

Exemple

Soit ${\displaystyle f(x)=5x^{2}+7x+8}$.

f est un polynôme du second degré, de coefficients a = 5, b = 7 et c = 8. Son discriminant est :

${\displaystyle \Delta =7^{2}-4\times 5\times 8=49-160=-111}$.

Discriminant et racines

On a déjà vu au chapitre précédent que la forme canonique d'une fonction trinôme fournit deux valeurs importantes dans son tableau de variations (les coordonnées du sommet de la parabole).

Rappel

La forme canonique de la fonction trinôme ${\displaystyle f(x)=ax^{2}+bx+c}$ est ${\displaystyle f(x)=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {\Delta }{4a^{2}}}\right]}$.

On peut d'ailleurs la retrouver en commençant par faire apparaître le début d'un carré parfait :

${\displaystyle {\begin{aligned}f(x)&=ax^{2}+bx+c\\&=a\left(x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}\right)\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}+{\frac {c}{a}}\right]\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}}{4a^{2}}}+{\frac {c}{a}}\right]\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b^{2}-4ac}{4a^{2}}}\right)\right]\\&=a\left[\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {\Delta }{4a^{2}}}\right].\end{aligned}}}$

Exemple

Donner la forme canonique des expressions suivantes :

• f(x) = x² + 5x + 5 ;
• g(x) = −3x² + 6x − 2.

Solution

f est une fonction du second degré avec a = 1, b = 5 et c = 5.

${\displaystyle f(x)=x^{2}+5x+5}$

or

${\displaystyle x^{2}+5x+{\frac {25}{4}}=(x+{\tfrac {5}{2}})^{2}}$

donc

${\displaystyle x^{2}+5x=(x+{\tfrac {5}{2}})^{2}-{\tfrac {25}{4}}}$

et par conséquent,

${\displaystyle {\begin{aligned}f(x)&=(x+{\tfrac {5}{2}})^{2}+5\\&=(x+{\tfrac {5}{2}})^{2}-{\tfrac {25}{4}}+{\tfrac {20}{4}}\\&=(x+{\tfrac {5}{2}})^{2}-{\tfrac {5}{4}}.\end{aligned}}}$

g est une fonction du second degré avec a = −3, b = 6 et c = −2.

${\displaystyle g(x)=-3x^{2}+6x-2=-3(x^{2}-2x)-2}$

or

${\displaystyle x^{2}-2x+1=(x-1)^{2}}$

donc

${\displaystyle x^{2}-2x=(x-1)^{2}-1}$

et par conséquent,

${\displaystyle {\begin{aligned}g(x)&=-3[(x-1)^{2}-1]-2\\&=-3(x-1)^{2}+3-2\\&=-3(x-1)^{2}+1.\end{aligned}}}$

 

Cette forme canonique permet en outre de trouver facilement les racines de ${\displaystyle f}$, c'est-à-dire résoudre l'équation ${\displaystyle (E)~:~f(x)=0}$ d'inconnue ${\displaystyle x}$.

En effet,

${\displaystyle (E)\Leftrightarrow a\left[\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {\Delta }{4a^{2}}}\right]=0}$

donc (comme ${\displaystyle a\neq 0}$)

${\displaystyle (E)\Leftrightarrow \left(x+{\frac {b}{2a}}\right)^{2}-{\frac {\Delta }{4a^{2}}}=0\Leftrightarrow \left(x+{\frac {b}{2a}}\right)^{2}={\frac {\Delta }{4a^{2}}}}$.

Sous cette forme, il est bien plus simple de résoudre l'équation en distinguant différents cas :

• si ${\displaystyle \Delta >0,~(E)\Leftrightarrow \left[x+{\frac {b}{2a}}={\sqrt {\frac {\Delta }{4a^{2}}}}{\text{ ou }}x+{\frac {b}{2a}}=-{\sqrt {\frac {\Delta }{4a^{2}}}}\right]\Leftrightarrow \left[x={\frac {-b+{\sqrt {\Delta }}}{2a}}{\text{ ou }}x={\frac {-b-{\sqrt {\Delta }}}{2a}}\right]}$ ;
• si ${\displaystyle \Delta =0,~(E)\Leftrightarrow x=-{\frac {b}{2a}}}$ ;
• si ${\displaystyle \Delta <0}$, il ne peut pas y avoir de racine réelle, puisqu’un carré ne peut pas être strictement négatif.

Finalement, voici ce qu’il faut absolument retenir :

Théorème

Le nombre de racines d'un trinôme dépend de son discriminant.

• Si ${\displaystyle \Delta >0}$ alors le trinôme a deux racines réelles :
  ${\displaystyle x_{1}={\frac {-b+{\sqrt {\Delta }}}{2a}}}$ et ${\displaystyle x_{2}={\frac {-b-{\sqrt {\Delta }}}{2a}}}$
• Si ${\displaystyle \Delta =0}$ alors le trinôme a une racine réelle :
  ${\displaystyle x_{0}=-{\frac {b}{2a}}}$
• Si ${\displaystyle \Delta <0}$ alors le trinôme n'a pas de racine réelle.

On remarque que dans le cas ${\displaystyle \Delta =0}$, ${\displaystyle x_{0}={\frac {-b+{\sqrt {\Delta }}}{2a}}={\frac {-b-{\sqrt {\Delta }}}{2a}}}$. On dit que la racine est double.

Conséquences graphiques

Interprétation graphique

Les racines de f correspondent aux abscisses des points d'intersection de ${\displaystyle {\mathcal {C}}}$, la courbe représentative de f, avec l’axe des abscisses (horizontal).

• Si ${\displaystyle \Delta <0}$ alors il n'y a pas d'intersection entre ${\displaystyle {\mathcal {C}}}$ et l’axe des abscisses.
• Si ${\displaystyle \Delta =0}$ alors ${\displaystyle {\mathcal {C}}}$ et l’axe des abscisses admettent un point d'intersection, de coordonnées ${\displaystyle \left(-{\frac {b}{2a}};0\right)}$
• Si ${\displaystyle \Delta >0}$ alors ${\displaystyle {\mathcal {C}}}$ et l’axe des abscisses admettent deux points d'intersection, de coordonnées ${\displaystyle \left({\frac {-b-{\sqrt {\Delta }}}{2a}};0\right)}$ et ${\displaystyle \left({\frac {-b+{\sqrt {\Delta }}}{2a}};0\right)}$

Les 6 cas qui peuvent se présenter

	Δ > 0	Δ = 0	Δ < 0
a > 0	Deux racines	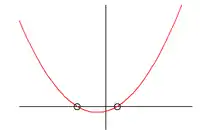Une racine	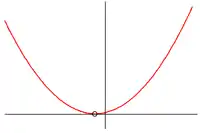Pas de racines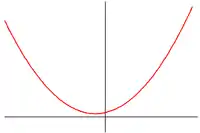
a < 0	Deux racines	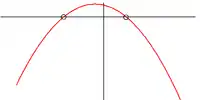Une racine	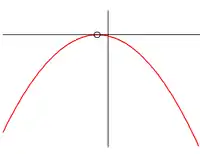Pas de racines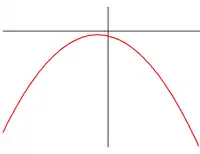

Exemples

Exemple détaillé

Calculer le discriminant puis les racines éventuelles des trinômes suivants.

• f(x) = 7x² + 6x − 1 ;
• g(x) = −3x² − 6x − 9.

Solution

f est un polynôme du second degré avec a = 7, b = 6 et c = −1.

${\displaystyle \Delta =b^{2}-4ac=6^{2}-4\times 7\times (-1)=36+28=64>0}$

donc f a deux racines :

${\displaystyle x_{1}={\frac {-b-{\sqrt {\Delta }}}{2a}}={\frac {-6-{\sqrt {64}}}{2\times 7}}={\frac {-6-8}{14}}={\frac {-14}{14}}=-1}$

et

${\displaystyle x_{2}={\frac {-b+{\sqrt {\Delta }}}{2a}}={\frac {-6+{\sqrt {64}}}{2\times 7}}={\frac {-6+8}{14}}={\frac {2}{14}}={\frac {1}{7}}}$.

g est un polynôme du second degré avec a = −3, b = −4 et c = −9.

${\displaystyle \Delta =b^{2}-4ac=(-4)^{2}-4\times (-3)\times (-9)=16-108=-92<0}$

donc g n'a aucune racine réelle.

 

Autres exemples

Calculer le discriminant puis les racines éventuelles des trinômes suivants. Vérifier la cohérence des résultats avec les courbes tracées plus haut.

• ${\displaystyle f_{1}:x\mapsto 2x^{2}+3x+1}$ ;
• ${\displaystyle f_{2}:x\mapsto x^{2}-2x+2}$ ;
• ${\displaystyle f_{3}:x\mapsto -x^{2}+3}$ ;
• ${\displaystyle f_{4}:x\mapsto -3x^{2}-x}$.

Solution

• ${\displaystyle f_{1}:x\mapsto 2x^{2}+3x+1}$

  ${\displaystyle \Delta =3^{2}-4\times 2\times 1=9-8=1>0}$ donc f₁ a deux racines réelles :

  ${\displaystyle x_{1}={\frac {-3-{\sqrt {1}}}{2\times 2}}=-{\frac {4}{4}}=-1}$ et

  ${\displaystyle x_{2}=-{\frac {2}{4}}=-{\frac {1}{2}}}$.

• ${\displaystyle f_{2}:x\mapsto x^{2}-2x+2}$

  ${\displaystyle \Delta =(-2)^{2}-4\times 1\times 2=4-8=-4<0}$ donc f₂ n'a aucune racine réelle.

• ${\displaystyle f_{3}:x\mapsto -x^{2}+3}$

  ${\displaystyle \Delta =0^{2}-4\times (-1)\times 3=12>0}$ donc f₃ a deux racines réelles :

  ${\displaystyle x_{1}={\frac {-0+{\sqrt {12}}}{2\times (-1)}}={\frac {2{\sqrt {3}}}{-2}}=-{\sqrt {3}}}$ et

  ${\displaystyle x_{2}={\frac {-0-{\sqrt {12}}}{2\times (-1)}}={\frac {-2{\sqrt {3}}}{-2}}={\sqrt {3}}}$.

• ${\displaystyle f_{4}:x\mapsto -3x^{2}-x}$

  ${\displaystyle \Delta =(-1)^{2}-4\times (-3)\times 0=1>0}$ donc f₄ a deux racines réelles :

  ${\displaystyle x_{1}={\frac {-(-1)+{\sqrt {1}}}{2\times (-3)}}={\frac {2}{-6}}=-{\frac {1}{3}}}$ et

  ${\displaystyle x_{2}={\frac {-(-1)-{\sqrt {1}}}{2\times (-3)}}={\frac {0}{-6}}=0}$.