Théorème des accroissements finis

En analyse, le théorème des accroissements finis (en abrégé : TAF) est à la fois une généralisation et un corollaire du théorème de Rolle. Pour toute fonction dérivable d'une variable réelle, son taux d'accroissement entre deux valeurs est réalisable comme pente d'une des tangentes à son graphe[1].

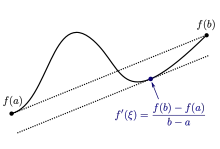
Il existe un point où la pente de la tangente est égale à la pente de la corde.

Fonction d'une variable réelle à valeurs réelles

Énoncé

Pour toute fonction réelle d'une variable réelle $f : [a, b] \to ℝ$ ( $a$ et $b$ réels tels que $a < b$ ), supposée continue sur l'intervalle fermé $[a, b]$ et dérivable sur l'intervalle ouvert $] a, b [$ , il existe un réel $c$ dans $] a, b [$ vérifiant :
${\frac {f(b)-f(a)}{b-a}}=f'(c).$

Graphiquement, le théorème des accroissements finis indique que, pour toute droite sécante en deux points à une courbe différentiable, il existe, entre ces deux points, une tangente parallèle à la sécante.

On peut illustrer ainsi le théorème : « Si un véhicule parcourt une distance à la vitesse moyenne de 60 km/h, alors son compteur (censé indiquer avec une précision infinie la vitesse instantanée) a indiqué au moins une fois la vitesse précise de 60 km/h. »

La solution $c$ n'est pas unique en général. Plus précisément, pour une fonction dérivable sur un intervalle $I$ , la solution $c$ est unique pour tous $a < b$ dans $I$ si et seulement si $f$ est strictement convexe ou strictement concave[2] sur $I$ .

Deux conséquences directes du théorème des accroissements finis sont :

le lien entre monotonie et signe de la dérivée ;
le théorème « limite de la dérivée » (si une fonction f, continue en a, est dérivable sauf peut-être en a, mais si sa dérivée a une limite finie au point a, alors f est en fait de classe C¹ en a).

Théorème des accroissements finis généralisé

Ce théorème s'applique dans le cas de deux fonctions continues sur $[a, b]$ et dérivables sur $] a, b [$ . Il assure[1] qu'il existe un réel $c$ de l'intervalle $] a, b [$ tel que

(f(b)-f(a))g'(c)=(g(b)-g(a))f'(c).

Il existe un point de l'arc paramétré où la tangente est parallèle à la corde.

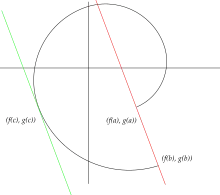
Géométriquement, il signifie que toute courbe représentative d'une fonction différentiable de ℝ dans ℝ², $t \mapsto (f (t), g (t))$ , possède une tangente parallèle à l'une quelconque de ses cordes.

Dans le cas où $g'$ ne s'annule pas sur $] a, b [$ , l'égalité peut s'écrire[1] :

{\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}.

Sous cette forme, le théorème est appelé théorème de la moyenne de Cauchy. Il peut être utilisé pour démontrer la règle de L'Hôpital.

Remarque: Si a = $-\infty$ ou b = $+\infty$ et si f et g sont dérivables sur ]a, b[ et possèdent en a et b des limites finies, notées f(a), f(b), g(a) et g(b), on obtient par la même méthode (en remplaçant le théorème de Rolle par une généralisation adaptée) une conclusion identique.

Généralisation aux courbes paramétrées dans l'espace

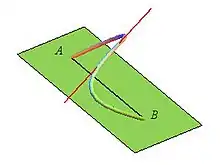
Exemple de tangente parallèle à un plan passant par A et B. Par contre, ici, aucune tangente n'est parallèle à [AB].

Pour tout triplet de fonctions $f,g,h$ réelles continues sur $[a,b]$ et dérivables sur $]a,b[$ , il existe $c\in \left]a,b\right[$ tel que le déterminant $\left\vert {\begin{array}{ccc}f'(c)&f(a)&f(b)\\g'(c)&g(a)&g(b)\\h'(c)&h(a)&h(b)\end{array}}\right\vert$ soit nul.

Si l'on pose $M(t)=(f(t),g(t),h(t))$ , $A=M(a)$ , $B=M(b)$ et $C=M(c)$ , le théorème énonce l'existence pour les courbes paramétrées joignant $A$ à $B$ d'une tangente (en un certain $C$ ), parallèle au plan $(OAB)$ , le déterminant nul indiquant la colinéarité des vecteurs ${\overrightarrow {OA}}$ , ${\overrightarrow {OB}}$ et ${\overrightarrow {OM}}'(c)$ .

Le point $O$ pouvant être choisi arbitrairement, il énonce en fait l'existence d'une corde $[CD]$ parallèle à un plan donné passant par $A$ et $B$ . Par contre, comme on le voit ci-contre, la généralisation qui consisterait à dire qu'il existe une tangente parallèle à $[AB]$ est fausse.

Notons que ce théorème contient le TAF généralisé, qui contient le TAF, lui-même contenant le théorème de Rolle.

Démonstration

Il suffit d'appliquer le théorème de Rolle à la fonction $\varphi$ définie par $\varphi \left(x\right)=\left\vert {\begin{array}{ccc}f(x)&f(a)&f(b)\\g(x)&g(a)&g(b)\\h(x)&h(a)&h(b)\end{array}}\right\vert$ qui vérifie $\varphi (a)=\varphi (b)(=0)$ , ainsi que $\varphi '\left(x\right)=\left\vert {\begin{array}{ccc}f'(x)&f(a)&f(b)\\g'(x)&g(a)&g(b)\\h'(x)&h(a)&h(b)\end{array}}\right\vert$ .

Inégalité des accroissements finis

L'inégalité des accroissements finis (IAF) :

Soit f : [a, b] → ℝ (avec a et b réels tels que a < b). Si :

f est continue sur l'intervalle fermé [a, b] ;

f est dérivable sur l'intervalle ouvert ]a, b[ ;

M est un réel tel que, pour tout élément x de ]a, b[, |f'(x)| ≤ M ;

alors[3] $\left|{{f(b)-f(a)} \over {b-a}}\right|\leq M$ ,

propriété que l'on peut illustrer par : « Si la vitesse instantanée d'un véhicule ne peut pas dépasser 120 km/h, alors sa vitesse moyenne non plus. »

Sous les mêmes hypothèses, f est donc M-lipschitzienne (car sa restriction à tout sous-intervalle de [a, b] vérifie encore les hypothèses). Remarquons que d'après le théorème des bornes, ces hypothèses sont vérifiées pour toute fonction f de classe C¹ sur [a, b], avec $M=\sup _{x\in \left[a,b\right]}\left|f'(x)\right|$ .

Il existe de même une « inégalité des accroissements finis généralisée » :

Soient f et g : [a, b] → ℝ continues sur [a,b] et dérivables sur ]a, b[, avec g' de signe constant. Si J est un intervalle de ℝ tel que, pour tout x de ]a, b[, f'(x) ∈ g'(x)J alors, f(b) – f(a) ∈ (g(b) – g(a))J.

On peut même démontrer directement, sans le théorème des accroissements finis, que cette conclusion reste vraie si la dérivabilité de f et g (et les hypothèses sur f'(x) et g'(x)) ne sont vérifiées que sur le complémentaire d'un ensemble dénombrable[4]^,[5]^,[6].

Théorème des accroissements finis et intégration

Une version intégrale du TAF est le théorème de la moyenne :
Pour toute fonction u à valeurs réelles, continue sur un segment [a, b] avec a < b, il existe un réel c de ]a, b[ tel que $u(c)={\frac {1}{b-a}}\int _{a}^{b}u(x)~\mathrm {d} x.$
L'analogue intégral du théorème des accroissements finis généralisé est un théorème de la moyenne généralisé :
Pour toutes fonctions u et v à valeurs réelles, continues sur un segment [a, b] avec a < b, v gardant un signe constant sur [a, b], il existe un réel c de $]a,b[$ tel que $u(c)\int _{a}^{b}v(x)~\mathrm {d} x=\int _{a}^{b}u(x)v(x)~\mathrm {d} x.$

Réciproque partielle

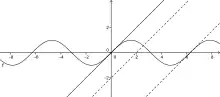
Pour la fonction sinus, la pente maximale des tangentes n'est pas la pente d'une corde.

Lorsque la valeur f'(c) = λ est atteinte en des points arbitrairement proches de c (ici : c = λ = 0), il arrive qu'aucune des cordes de pente λ ne traverse l'axe x = c.

Puisque le théorème des accroissements finis garantit que (pour une fonction $f$ vérifiant les hypothèses) tout taux d'accroissement est un nombre dérivé, une question naturelle est : réciproquement, tout nombre dérivé est-il un taux d'accroissement ?

La réponse est : non. Par exemple (cf. figure ci-contre), pour la fonction ${\displaystyle \sin$ , le nombre dérivé $\sin '\left(0\right)=\cos \left(0\right)=1$ n'est pas un taux d'accroissement. Mais la pathologie de ce cas ( $1$ est ici la valeur maximum de $f'$ ) est la seule obstruction.

Le théorème des accroissements finis possède en effet la réciproque partielle suivante (réciproque « faible[7] ») :

Pour toute fonction $f$ dérivable sur un intervalle, toute valeur non extrémale de $f'$ est un taux d'accroissement de $f$ [8].

Autrement dit : toute tangente au graphe de $f$ dont la pente $f'(c)$ n'est ni maximum, ni minimum, possède une parallèle sécante au graphe en deux points. Le TAF permet en outre d'affirmer[8] que si la valeur $f'(c)$ n'est atteinte qu'au point $c$ , alors les deux extrémités de la corde sont de part et d'autre du point de tangence[7] (réciproque « forte »).

La « réciproque faible » ci-dessus se déduit du lemme suivant, qui (joint au TAF lui-même) permet aussi de démontrer que toute fonction dérivée vérifie la propriété des valeurs intermédiaires :

Pour toute fonction

f

dérivable sur un intervalle, tout réel strictement compris entre deux nombres dérivés de

f

est un taux d'accroissement de

f

[8].

La « réciproque forte » se localise facilement : pour toute fonction $f$ dérivable sur un intervalle, si $\lambda =f'(c)$ n'est pas un extremum local de $f'$ et si, au voisinage de $c$ , la valeur $\lambda$ n'est atteinte par $f'$ qu'en $c$ , alors $\lambda$ est encore un taux d'accroissement de $f$ entre deux points $x$ et $y$ tels que $x<c<y$ [7]. (Pour la nécessité de la seconde hypothèse, cf. figure ci-contre.)

Pour le théorème des accroissements finis généralisés, on démontre de même des réciproques analogues[9].

Fonction d'une variable vectorielle à valeurs réelles

Soient $\Omega$ un ouvert d'un espace vectoriel normé E (par exemple E = ℝⁿ, ce qui inclut le cas E = ℂ identifié à ℝ²), $x$ un point de $\Omega$ et $h$ un vecteur non nul de E tel que $[x,x+h]\subset \Omega$ , et $f:\Omega \to \mathbb {R}$ une fonction continue sur $[x,x+h]$ et différentiable suivant le vecteur h sur $]x,x+h[$ . Alors il existe $\xi \in ]x,x+h[$ tel que

f(x+h)-f(x)=D_{h}f(\xi ),

par simple application du théorème des accroissements finis à la fonction composée $[0,1]\to \mathbb {R} ,\;t\mapsto f(x+th)$ .

Fonction à valeurs vectorielles

Pour une telle fonction, il n'existe pas d'analogue du théorème (avec égalité) des accroissements finis, ni même de son cas particulier qu'est le théorème de Rolle (cf. § Remarques de l'article sur ce théorème).

À défaut, lorsque l'espace d'arrivée de f est ℝⁿ, on peut appliquer le théorème des accroissements finis à chacune des composantes réelles f_k de la fonction f = (f₁, … , f_n), mais les c_k que l'on construit ainsi (ou les ξ_k comme ci-dessus si la variable est vectorielle) n'ont aucune raison d'être égaux.

On peut cependant établir une inégalité des accroissements finis dans ce cadre.

Inégalité des accroissements finis

Soient $a < b$ deux réels, E un espace localement convexe et deux fonctions
$f:[a,b]\to E\quad {\text{et}}\quad g:[a,b]\to \mathbb {R}$
supposées continues sur $[a, b]$ et dérivables sur $] a, b [$ .

Si $g'$ est de signe constant alors, pour tout sous-ensemble convexe fermé A de E tel que
$\forall t\in ]a,b[\quad f'(t)\in g'(t)A,$
on a :
$f(b)-f(a)\in (g(b)-g(a))A.$

Lorsque $g'$ est non seulement de signe constant mais à valeurs non nulles, la conclusion se reformule en :

{\frac {f(b)-f(a)}{g(b)-g(a)}}\in {\overline {\text{Co}}}\left(\left\{{\frac {f'(t)}{g'(t)}},~t\in ]a,b[\right\}\right),

où « $Co$ » désigne l'enveloppe convexe fermée.

En particulier si $g$ (t) = t, on obtient[10] : f(b) – f(a) ∈ (b – a)Co({f'(t), t ∈ [a, b]}).

Remarques.

Ce théorème est d'autant plus surprenant qu’il n'existe pas de théorème de Rolle vectoriel, ou, ce qui revient au même, il n’y a pas d'égalité des accroissements finis mais seulement une inégalité, comme en témoigne la fonction définie par $f (t) = e i t$ qui satisfait $f (0) = f (2π)$ alors que sa dérivée ne s'annule pas sur $[0, 2π]$ .
Il en découle qu’une fonction dérivable dont la dérivée est nulle ne peut être que constante.
Il se déduit directement de son homologue pour les fonctions à valeurs réelles, en utilisant le théorème de Hahn-Banach[11] ou sa version géométrique qu'est le théorème d'Eidelheit[12].
Sa conclusion reste valide, avec une démonstration identique, sous des hypothèses plus faibles :
- il suffit que f'(t) et g'(t) existent (et vérifient les propriétés indiquées) pour t appartenant au complémentaire d'un ensemble dénombrable[11] ;
- pour f, la continuité et la différentiabilité peuvent être prises au sens faible[12].

Corollaire

On en déduit immédiatement le corollaire suivant (qui se démontre aussi directement[13]^,[14]^,[15]) :

Soient $a < b$ deux réels, E un espace vectoriel normé et deux fonctions
$f:\left[a,b\right]\to E\quad {\text{et}}\quad g:[a,b]\to \mathbb {R}$
supposées continues sur $[a, b]$ et dérivables sur $] a, b [$ .

Si
$\forall t\in \left]a,b\right[\quad \|f'(t)\|\leq g'(t)$
alors
$\|f(b)-f(a)\|\leq g(b)-g(a).$

En particulier si, pour une certaine constante $M$ (nécessairement positive ou nulle), on a

\forall t\in \left]a,b\right[\quad \|f'(t)\|\leq M

alors

\|f(b)-f(a)\|\leq M(b-a).

Fonction d'une variable vectorielle à valeurs vectorielles

Le corollaire précédent permet de majorer l'accroissement d'une fonction différentiable si l'on connaît une majoration de sa différentielle. Plus précisément[16] :

Soient E et F deux espaces vectoriels normés réels, U un ouvert de E et $f$ : U → F une application différentiable. Pour tout segment $[a, b]$ inclus dans U, on a :
$\|f(b)-f(a)\|_{F}\leq \left(\sup _{x\in [a,b]}\|f\,{'}(x)\|\right)\|b-a\|_{E}$
où, pour tout point $x$ de U, $║ f ' (x)║$ est la norme d'opérateur de la différentielle de $f$ au point $x$ .

Ce corollaire est une conséquence immédiate du précédent, appliqué à la fonction de la variable réelle $[0,1]\to F,\,t\mapsto f\left[(1-t)a+tb\right].$

Il n'a bien sûr d'intérêt que si le $sup$ qu'il fait intervenir est fini, c'est-à-dire si la différentielle de $f$ est bornée sur $[a, b]$ . Cette condition est assurée en particulier si $f$ est de classe C¹ sur U.

Il se généralise à tout ouvert U connexe et à toute fonction dont la différentielle est bornée par k. Si $d U (a, b)$ est la borne inférieure des longueurs des lignes polygonales joignant $a$ à $b$ et incluses dans U, on a

\|f(b)-f(a)\|_{F}\leq kd_{U}(a,b).

Polynôme sur un corps réel clos

Soit $R$ un corps réel clos. Si $a<b\in R$ , on note, tout comme dans $\mathbb {R}$ , $]a,b[$ l'ensemble $\lbrace x\in R|a<x<b\rbrace$ . Alors[17] :

Soit $P\in R[X]$ et $a<b\in R$ . Il existe $c\in ]a,b[$ tel que :
$P(b)-P(a)=(b-a)P'(c)$

Application en cinématique

En cinématique, pour déterminer l'orientation de la tangente, on utilise la corde.
Il s'écoule 0,04 s entre le relevé de deux points.

En cinématique, le vecteur vitesse d'un point d'un mobile est tangent à la trajectoire de ce point. À partir d'un enregistrement du mouvement (succession de positions relevées à intervalle de temps constant), on peut déterminer la direction du vecteur vitesse au point i en considérant la corde (M_i-1M_i+1).

En effet, sur un petit intervalle, la pente de la tangente varie peu, donc on estime que la valeur en M_i vérifie le théorème des accroissements finis.

Notes et références

Cet article est partiellement ou en totalité issu de l'article intitulé « Inégalité des accroissements finis pour les fonctions à valeurs vectorielles » (voir la liste des auteurs).

Pour une démonstration, voir par exemple « Théorème des accroissements finis » sur Wikiversité.
Voir cet exercice corrigé de la leçon « Fonctions d'une variable réelle » sur Wikiversité.
Pour une démonstration, voir par exemple « Inégalité des accroissements finis » sur Wikiversité.
(en) Andreas Kriegl et Peter W. Michor (de), The Convenient Setting of Global Analysis, AMS, 1997, 618 p. (ISBN 978-0-8218-0780-4, lire en ligne), p. 10.
(en) Stephen D. Casey et Richard Holzsager, « On Positive Derivatives and Monotonicity », Missouri J. Math. Sci., vol. 17, n^o 3,‎ 2005, p. 161-173 (lire en ligne).
Démonstration dans « Inégalité des accroissements finis généralisée » sur Wikiversité.
Propriété redémontrée par (en) Jingcheng Tong et Peter A. Braza, « A converse of the mean value theorem », Amer. Math. Monthly, vol. 104, n^o 10,‎ 1997, p. 939-942 (JSTOR 2974475) et à nouveau (plus simplement) par (en) Cristinel Mortici, « A converse of the mean value theorem made easy », Int. J. Math. Educ. Sci. Tech., vol. 42, n^o 1,‎ 2011, p. 89-91 (lire en ligne).
Pour une démonstration, voir par exemple la page sur le théorème de Darboux sur Wikiversité.
Mortici 2011.
Théorème 2.1 de (en) Robert H. Martin, Jr., Nonlinear Operators and Differential Equations in Banach Spaces, John Wiley & Sons, 1976, p. 26, cité dans (en) J. M. Ayerbe Toledano, T. Domínguez Benavides et G. López Acedo, Measures of Noncompactness in Metric Fixed Point Theory, Springer, coll. « Operator Theory: Advances and Applications » (n^o 99), 1997, 211 p. (ISBN 978-3-7643-5794-8, lire en ligne), p. 16.
(en) Andreas Kriegl et Peter W. Michor (de), The Convenient Setting of Global Analysis, AMS, 1997, 618 p. (ISBN 978-0-8218-0780-4, lire en ligne), p. 10 : Mean value theorem.
(en) Jerzy Albrycht (pl), « L'Hôpital's rule for vector-valued functions », Colloquium Mathematicum, vol. 2, n^os 3-4,‎ 1951, p. 176-177 (lire en ligne) : Cauchy's Mean Value Theorem.
Sylvie Benzoni-Gavage, Calcul différentiel et équations différentielles : cours et exercices corrigés, Dunod, 2014, 2^e éd. (lire en ligne), p. 29-31.
« Théorème : Inégalité des accroissements finis pour les fonctions à valeurs vectorielles » sur Wikiversité.
La démonstration directe ne nécessite que l'existence de dérivée à droite pour les fonctions $g$ et $f$ : Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques, t. 2 : Analyse, Bordas, 1977, p. 132-133. On peut de plus supposer seulement que ces dérivées à droite existent (et satisfont l'inégalité) sur le complémentaire d'un ensemble dénombrable : Jean-Pierre Ramis, André Warusfel et al., Mathématiques Tout-en-un pour la Licence 2, Dunod, 2014, 2^e éd. (lire en ligne), p. 602, th. 88.
Benzoni-Gavage 2014, p. 31.
(en) Jacek Bochnak, Michel Coste et Marie-Françoise Roy, « Ordered Fields, Real Closed Fields », dans Real Algebraic Geometry, Springer, coll. « Ergebnisse der Mathematik und ihrer Grenzgebiete / A Series of Modern Surveys in Mathematics », 1998 (ISBN 978-3-662-03718-8, DOI 10.1007/978-3-662-03718-8_2, lire en ligne), p. 7–21

Voir aussi

Article connexe

Le théorème de la corde universelle, qui étudie l'existence d'une corde parallèle à la base, au lieu d'une tangente.

Bibliographie

Joseph-Louis Lagrange, « Théorie des fonctions analytiques contenant les principes du calcul différentiel, dégagés de toute considération d'infiniment petits ou d'évanouissants, de limites ou de fluxions et réduits à l'analyse algébrique des quantités finies », Journal de l'École polytechnique, 9^e cahier, t. III, 1797, § 52, p. 49
Hélène Gispert-Chambaz, Camille Jordan et les fondements de l'analyse, Publications mathématiques d'Orsay, Université de Paris-Sud, 1982. Selon cet auteur (p. 44), le premier traité d'analyse présentant une démonstration correcte du théorème des accroissements finis (et identique à la présentation moderne) est celui de Dini, paru en Italie en 1878.

Lien externe

« Théorème des accroissements finis », sur uel.unisciel.fr

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[V:TAF-1] Pour une démonstration, voir par exemple « Théorème des accroissements finis » sur Wikiversité.

[Wikiversité-2] Voir cet exercice corrigé de la leçon « Fonctions d'une variable réelle » sur Wikiversité.

[3] Pour une démonstration, voir par exemple « Inégalité des accroissements finis » sur Wikiversité.

[4] (en) Andreas Kriegl et Peter W. Michor (de), The Convenient Setting of Global Analysis, AMS, 1997, 618 p. (ISBN 978-0-8218-0780-4, lire en ligne), p. 10.

[5] (en) Stephen D. Casey et Richard Holzsager, « On Positive Derivatives and Monotonicity », Missouri J. Math. Sci., vol. 17, n^o 3,‎ 2005, p. 161-173 (lire en ligne).

[6] Démonstration dans « Inégalité des accroissements finis généralisée » sur Wikiversité.

[TongBrazaMortici-7] Propriété redémontrée par (en) Jingcheng Tong et Peter A. Braza, « A converse of the mean value theorem », Amer. Math. Monthly, vol. 104, n^o 10,‎ 1997, p. 939-942 (JSTOR 2974475) et à nouveau (plus simplement) par (en) Cristinel Mortici, « A converse of the mean value theorem made easy », Int. J. Math. Educ. Sci. Tech., vol. 42, n^o 1,‎ 2011, p. 89-91 (lire en ligne).

[V:Darboux-8] Pour une démonstration, voir par exemple la page sur le théorème de Darboux sur Wikiversité.

[9] Mortici 2011.

[10] Théorème 2.1 de (en) Robert H. Martin, Jr., Nonlinear Operators and Differential Equations in Banach Spaces, John Wiley & Sons, 1976, p. 26, cité dans (en) J. M. Ayerbe Toledano, T. Domínguez Benavides et G. López Acedo, Measures of Noncompactness in Metric Fixed Point Theory, Springer, coll. « Operator Theory: Advances and Applications » (n^o 99), 1997, 211 p. (ISBN 978-3-7643-5794-8, lire en ligne), p. 16.

[KM-11] (en) Andreas Kriegl et Peter W. Michor (de), The Convenient Setting of Global Analysis, AMS, 1997, 618 p. (ISBN 978-0-8218-0780-4, lire en ligne), p. 10 : Mean value theorem.

[A-12] (en) Jerzy Albrycht (pl), « L'Hôpital's rule for vector-valued functions », Colloquium Mathematicum, vol. 2, n^os 3-4,‎ 1951, p. 176-177 (lire en ligne) : Cauchy's Mean Value Theorem.

[13] Sylvie Benzoni-Gavage, Calcul différentiel et équations différentielles : cours et exercices corrigés, Dunod, 2014, 2^e éd. (lire en ligne), p. 29-31.

[14] « Théorème : Inégalité des accroissements finis pour les fonctions à valeurs vectorielles » sur Wikiversité.

[15] La démonstration directe ne nécessite que l'existence de dérivée à droite pour les fonctions $g$ et $f$ : Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques, t. 2 : Analyse, Bordas, 1977, p. 132-133. On peut de plus supposer seulement que ces dérivées à droite existent (et satisfont l'inégalité) sur le complémentaire d'un ensemble dénombrable : Jean-Pierre Ramis, André Warusfel et al., Mathématiques Tout-en-un pour la Licence 2, Dunod, 2014, 2^e éd. (lire en ligne), p. 602, th. 88.

[16] Benzoni-Gavage 2014, p. 31.

[17] (en) Jacek Bochnak, Michel Coste et Marie-Françoise Roy, « Ordered Fields, Real Closed Fields », dans Real Algebraic Geometry, Springer, coll. « Ergebnisse der Mathematik und ihrer Grenzgebiete / A Series of Modern Surveys in Mathematics », 1998 (ISBN 978-3-662-03718-8, DOI 10.1007/978-3-662-03718-8_2, lire en ligne), p. 7–21