Fonction convexe

En mathématiques, une fonction réelle d'une variable réelle est dite convexe si :

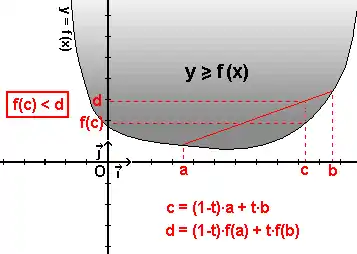
quels que soient deux points A et B du graphe de la fonction, le segment [AB] est entièrement situé au-dessus du graphe, c’est-à-dire que la courbe représentative de la fonction se situe toujours en dessous de ses cordes, ou
l'épigraphe de la fonction (l'ensemble des points qui sont au-dessus de son graphe) est un ensemble convexe, ou
vu d'en dessous, le graphe de la fonction est en bosse.

Fonction convexe.

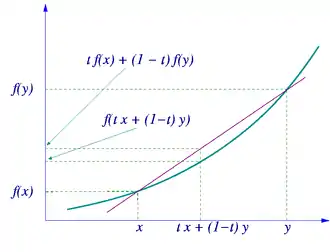
En précisant au moyen des valeurs de la fonction ce que sont les points A et B ci-dessus, on obtient une définition équivalente souvent donnée de la convexité d'une fonction : une fonction définie sur un intervalle réel $I$ est convexe lorsque, pour tous $x$ et $y$ de $I$ et tout $t$ dans $[0; 1]$ on a :

f\left(tx+(1-t)y\right)\leq t\,f(x)+(1-t)\,f(y).

Lorsque l'inégalité est stricte (avec $x$ différent de $y$ et $t$ dans $]0; 1[$ ), on parle de fonction strictement convexe.

La fonction carré et la fonction exponentielle sont des exemples de fonctions strictement convexes sur ℝ.

Ces définitions se généralisent aux fonctions définies sur un espace vectoriel (ou affine) arbitraire et à valeurs dans la droite réelle achevée ${\overline {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}$ .

À l'inverse, une fonction dont un même segment [AB] est situé en dessous du graphe, ou dont l'hypographe (l'ensemble des points qui sont en dessous du graphe de la fonction) est un ensemble convexe, ou encore dont, vu d'en dessous, le graphe est en creux, est dite concave. En d'autres termes, une fonction $f$ est concave si son opposée $-f$ est convexe. Ainsi, les fonctions affines sont à la fois convexes et concaves.

Les fonctions convexes sont, avec les ensembles convexes, les objets constitutifs de l'analyse convexe, une discipline « intermédiaire » entre l'algèbre linéaire et l'analyse non linéaire. Elles permettent de démontrer un grand nombre d'inégalités remarquables, dites inégalités de convexité. Elles jouent aussi un rôle singulier en optimisation, en supprimant la distinction entre minima locaux et globaux (tout minimum local d'une fonction convexe est un minimum global).

Fonction convexe d'une variable réelle

Dans cette première section, on va supposer que l'ensemble de départ est un intervalle réel $I$ . Cette restriction permet de fournir une première initiation aux fonctions convexes d'abord plus aisée et parce que la possibilité de tracer des représentations graphiques planes facilite certainement la tâche, ensuite et surtout parce que les concepts de continuité ou dérivabilité sont significativement plus maniables pour les fonctions d'une seule variable. Cette approche montre tout de même vite ses limites, en particulier parce qu'elle n'est guère pertinente pour appliquer la théorie des fonctions convexes à l'optimisation qui en est sans doute la principale motivation.

Définitions

Définition — Une fonction $f$ d'un intervalle réel $I$ vers ℝ est dite convexe lorsque, pour tous $x 1$ et $x 2$ de $I$ et tout $t$ dans $[0; 1]$ on a :

f(t\,x_{1}+(1-t)\,x_{2})\leq t\,f(x_{1})+(1-t)\,f(x_{2}).

Cela signifie que pour tout $x 1$ et $x 2$ de $I$ , le segment $[A 1, A 2]$ de ℝ², où $A 1 = (x 1, f (x 1))$ et $A 2 = (x 2, f (x 2))$ , est situé au-dessus de la courbe représentative de $f$ .

Une fonction concave est une fonction dont la fonction opposée est convexe.

On vérifie aussitôt ce qui suit, reliant les notions d'ensemble convexe et de fonction convexe :

Remarque — La fonction $f$ est convexe sur $I$ si et seulement si son épigraphe $\operatorname {epi} \,f:=\{(x,\,y)\in I\times \mathbb {R} \mid y\geq f(x)\}$ est un sous-ensemble convexe de ℝ².

Exemple: La fonction $x \mapsto | x |$ est convexe, parce que son épigraphe est un quart de plan (lui-même convexe comme intersection de deux demi-plans). Il est souvent malcommode de vérifier la convexité d'une fonction définie par une formule concrète à partir de la seule définition, on attendra donc quelques paragraphes pour donner d'autres exemples, lorsqu'on disposera d'un critère de convexité plus utilisable en pratique.

Possibilité de n'utiliser que des milieux

La définition de la convexité fait apparaître des barycentres où les coefficients sont des réels arbitraires de $[0; 1]$ . Lorsqu'on ne fait porter l'hypothèse que sur les milieux, elle s'étend aux isobarycentres :

Lemme[1] — Si $f$ vérifie la condition suivante pour $p = 2$ , alors elle la vérifie pour tout entier $p \geq 2$ :

\forall x_{1},\cdots ,x_{p}\in I\quad f\left({\frac {x_{1}+\cdots +x_{p}}{p}}\right)\leq {\frac {f(x_{1})+\cdots +f(x_{p})}{p}}.

Démonstration[2]

Le « principe de récurrence alternatif » suivant démontre ce lemme.

Si la condition est vraie pour $p$ alors elle l'est pour $2 p$ car

{\begin{aligned}f\left({\frac {x_{1}+\cdots +x_{2p}}{2p}}\right)&=f\left({\frac {{\frac {x_{1}+\cdots +x_{p}}{p}}+{\frac {x_{p+1}+\cdots +x_{2p}}{p}}}{2}}\right)\\&\leq {\frac {f\left({\frac {x_{1}+\cdots +x_{p}}{p}}\right)+f\left({\frac {x_{p+1}+\cdots +x_{2p}}{p}}\right)}{2}}\\&\leq {\frac {{\frac {f(x_{1})+\cdots +f(x_{p})}{p}}+{\frac {f(x_{p+1})+\cdots +f(x_{2p})}{p}}}{2}}\\&={\frac {f(x_{1})+\cdots +f(x_{2p})}{2p}}.\end{aligned}}

Si elle l'est pour p + 1 alors elle l'est pour p car en posant

x_{p+1}={\frac {x_{1}+\cdots +x_{p}}{p}},

on obtient

f(x_{p+1})=f\left({\frac {x_{1}+\cdots +x_{p+1}}{p+1}}\right)\leq {\frac {f(x_{1})+\cdots +f(x_{p+1})}{p+1}},

c'est-à-dire

f(x_{p+1})\leq {\frac {f(x_{1})+\cdots +f(x_{p})}{p}}.

En ajoutant une hypothèse supplémentaire de régularité[3] de $f$ , on obtient :

Proposition[4] — Une fonction $f$ continue sur $I$ est convexe sur $I$ si (et seulement si) quels que soient les éléments $x 1$ et $x 2$ de $I$ :

f\left({\frac {x_{1}+x_{2}}{2}}\right)\leq {\frac {f(x_{1})+f(x_{2})}{2}}.

Démonstration[5]

Grâce au lemme, on a

\forall x,y\in I\quad f\left(tx+(1-t)y\right)\leq tf(x)+(1-t)f(y)

pour tout rationnel $t$ dans $[0; 1]$ donc (par densité) pour tout $t$ dans $[0; 1]$ .

Extension à des barycentres de plus de deux points

L'inégalité de la définition s'étend comme suit (on peut le démontrer par récurrence sur l'entier p[6] ou par le même argument que dans la proposition ci-dessus[7]. On dénomme parfois cette version l'inégalité de Jensen :

Proposition — Si $f$ est convexe sur $I$ et si $x 1, \dots , x p$ sont des points de $I$ et $t 1, \dots , t p$ des réels positifs ou nuls tels que $t 1 + \dots + t p = 1$ , alors :

f(t_{1}\,x_{1}+\cdots +t_{p}\,x_{p})\leq t_{1}\,f(x_{1})+\cdots +t_{p}\,f(x_{p}).

Géométrie du graphe d'une fonction convexe

On appelle parfois « lemme des trois cordes » ou « inégalité des pentes » voire « inégalité des trois pentes » le résultat suivant[8] :

Proposition[9] — Si $f$ est convexe sur $I$ pour tous points $x 1$ , $x 2$ et $x 3$ de $I$ avec $x 1 < x 2 < x 3$

{\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}\leq {\frac {f(x_{3})-f(x_{1})}{x_{3}-x_{1}}}\leq {\frac {f(x_{3})-f(x_{2})}{x_{3}-x_{2}}}.

Réciproquement, si l'une des deux inégalités est vérifiée pour tous $x 1$ , $x 2$ et $x 3$ de $I$ avec $x 1 < x 2 < x 3$ , alors $f$ est convexe.

Régularité des fonctions convexes

Le « lemme des trois cordes » permet de montrer que[10] :

Théorème — Si $I$ est un intervalle ouvert et si $f : I \to ℝ$ est convexe alors :

$f$ est dérivable à gauche et à droite (donc continue) et $f g' \leq f d'$ ;
les fonctions $f g'$ , $f d'$ sont croissantes ;
l'ensemble des points $x$ où $f$ n'est pas dérivable (c'est-à-dire tels que $f g' (x) \neq f d' (x)$ ) est au plus dénombrable.

Démonstration

Soit $a \in I$ . On définit sur $I \ {a}$ le taux d'accroissement en $a$ par $\tau _{a}:x\mapsto {\frac {f(x)-f(a)}{x-a}}$ . Cette fonction est croissante d'après le lemme des trois cordes appliqué aux trois cas : $a < x < y$ , $x < a < y$ et $x < y < a$ . Elle admet donc en $a$ une limite à gauche $f g' (a) > -\infty$ et une limite à droite $f d' (a) < +\infty$ telles que $f g' (a) \leq f d' (a)$ .
Soient $x, y \in I$ tels que $x < y$ . Pour tous $s, t \in I$ tels que $x \neq s < y$ et $x < t \neq y$ , $τ x (s) \leq τ x (y) = τ y (x) \leq τ y (t)$ . En faisant tendre $s$ vers $x \pm$ et $t$ vers $y \pm$ , on en déduit : $f g' (x), f d' (x) \leq f g' (y), f d' (y)$ . En particulier, les fonctions $f g'$ et $f d'$ sont croissantes.
La fonction $f d'$ étant croissante, d'après le théorème de Froda, l'ensemble de ses points de discontinuité est au plus dénombrable. Montrons qu'en tout point $x$ où elle est continue, elle coïncide avec $f g'$ , autrement dit : $f$ est dérivable en $x$ . D'après les inégalités précédentes, pour tout $s \in I$ tel que $s < x$ , on a $f d' (s) \leq f g' (x) \leq f d' (x)$ . Alors, par continuité de $f d'$ en $x$ et le théorème des gendarmes, en faisant tendre $s$ vers $x$ , il suit que $f g' (x) = f d' (x)$ .

On démontre par ailleurs (voir infra) que $f$ est aussi localement lipschitzienne.

Cas des fonctions dérivables

La fonction

x\mapsto x^{3}

est convexe sur ℝ₊ et concave sur ℝ_–.

On dispose de deux caractérisations[11] :

Proposition — Soit $f$ une fonction dérivable sur un intervalle $I$ .

$f$ est convexe si et seulement si sa courbe représentative est au-dessus de chacune de ses tangentes ;
$f$ est convexe si et seulement si sa dérivée est croissante sur $I$ .

On déduit de la seconde caractérisation :

que toute fonction convexe et dérivable (sur un intervalle réel) est de classe C¹[12] ;
le corollaire suivant, fort pratique pour vérifier sans mal la convexité d'exemples spécifiques :

Corollaire[13] — Soit $f$ une fonction deux fois dérivable sur un intervalle $I$ .

$f$ est convexe si et seulement si sa dérivée seconde $f''$ est à valeurs positives ou nulles.

Ainsi, on peut désormais facilement ajouter à sa collection de fonctions convexes (ou concaves) les exemples suivants :

la fonction puissance $\mathbb {R} _{+}^{*}\to \mathbb {R} ,\,x\mapsto x^{a}$ est concave si $0 < a < 1$ et convexe sinon ;
pour tout entier positif $n$ , la fonction $\mathbb {R} \to \mathbb {R} ,\,x\mapsto x^{n}$ est convexe si $n$ est pair (si $n$ est impair, elle est convexe sur ℝ₊ et concave sur ℝ_–) ;
la fonction $ℝ \to ℝ, x \mapsto exp(x)$ est convexe ;
la fonction $ℝ * + \to ℝ, x \mapsto ln(x)$ est concave.

Stricte convexité

En faisant intervenir des inégalités strictes, on dispose d'une variante de la convexité : la stricte convexité.

Définition — Une fonction $f$ d'un intervalle $I$ de ℝ vers ℝ est dite strictement convexe lorsque, pour tous $x 1$ et $x 2$ distincts dans $I$ et tout $t$ dans $]0; 1[$ , on a :

f(t\,x_{1}+(1-t)\,x_{2})<t\,f(x_{1})+(1-t)\,f(x_{2}).

Les résultats énoncés plus haut pour des fonctions convexes s'adaptent généralement sans mal aux fonctions strictement convexes.

De même que les fonctions dérivables convexes sont celles qui ont une dérivée croissante, les fonctions dérivables strictement convexes sont celles qui ont une dérivée strictement croissante.

D'après le lien entre monotonie et signe de la dérivée, une fonction $f$ deux fois dérivable est donc strictement convexe si et seulement si $f''$ est positive et ne s'annule que sur un ensemble d'intérieur vide.

Exemple: $x \mapsto x 4$ est strictement convexe (sa dérivée seconde est positive et ne s'annule qu'en $0$ ).

Fonction convexe définie sur un espace vectoriel

Convexité

On peut donner au moins deux définitions légèrement différentes d'une fonction convexe de plusieurs variables réelles (ou plus généralement : d'une variable vectorielle), qui reviennent essentiellement au même mais ne fournissent néanmoins pas exactement les mêmes fonctions. On prendra donc garde au contexte lors d'une invocation d'une de ces définitions pour comprendre s'il s'agit ou non de fonctions susceptibles de prendre des valeurs infinies.

Définition 1 — Soient $E$ un espace vectoriel (ou affine) réel et $C$ un convexe de $E$ . On dit qu'une fonction

f:C\to \mathbb {R}

est convexe lorsque

pour tous

x 1

et

x 2

de

C

et tout

t

dans

[0; 1]

, on a :

f(tx_{1}+(1-t)x_{2})\leq tf(x_{1})+(1-t)f(x_{2})

.

Autrement dit : $f$ est convexe si sa « restriction » $t \mapsto f (tA + (1 - t) B)$ à tout segment $[A,B]\subset C$ est une fonction convexe de la variable réelle $t \in [0; 1]$ (voir supra)[14].

Définition 2 — Soit

E

un espace vectoriel (ou affine) réel. On dit qu'une fonction

f:E\to \mathbb {R} \cup \{+\infty \}

est convexe lorsquepour tous

x 1

et

x 2

de

dom f

{\displaystyle

et tout

t

dans

[0; 1]

, on a :

f(tx_{1}+(1-t)x_{2})\leq tf(x_{1})+(1-t)f(x_{2})

.

Étant donnée une fonction convexe au sens de la définition 1, on peut lui associer une fonction convexe au sens de la définition 2 en la prolongeant hors de $C$ par la valeur $+\infty$ ; réciproquement, étant donnée une fonction convexe $f:E\to \mathbb {R} \cup \{+\infty \}$ au sens de la définition 2, l'ensemble $C := dom f$ est un convexe et la restriction de $f$ à $C$ est une fonction convexe au sens de la définition 1. Les deux transformations sont réciproques l'une de l'autre : les deux définitions, quoique techniquement distinctes, décrivent bien la même notion.

Certaines sources requièrent de plus que $C$ soit non vide (dans la définition 1) ou que $f$ ne soit pas la constante $+\infty$ (dans la définition 2) pour prévenir certaines exceptions désagréables dans quelques énoncés. Une telle fonction de $E$ dans $\mathbb {R} \cup \{+\infty \}$ est dite propre[15].

La définition 2 est plus récente que la définition 1 et fut introduite indépendamment par Rockafellar et Moreau[16]. Elle permet de définir une fonction convexe comme un seul « objet » (une fonction définie sur un espace vectoriel ayant une propriété bien particulière) et non comme un couple formé d'un ensemble convexe d'un espace vectoriel et d'une fonction à valeurs réelles définie sur cet ensemble convexe. La définition 2 est la plus communément utilisée en analyse convexe, pour les raisons suivantes : d'une part, elle allège souvent l'expression des résultats et, d'autre part, elle permet de ne pas devoir préciser le convexe sur lequel est définie une fonction convexe obtenue par l'une des constructions standards de l'analyse convexe, comme l'enveloppe supérieure, la fonction d'appui, la fonction marginale, la fonction conjuguée, la fonction duale en optimisation, etc.

Stricte convexité

Soit $E$ un espace vectoriel (ou affine) réel. On dit qu'une fonction $f:E\to \mathbb {R} \cup \{+\infty \}$ est strictement convexe si, pour tous $x 1$ et $x 2$ distincts dans $dom f$ et tout $t$ dans $]0; 1[$ , on a :

f(t\,x_{1}+(1-t)\,x_{2})<t\,f(x_{1})+(1-t)\,f(x_{2}).

Forte convexité

Soit $(E, ║∙║)$ un espace normé. On dit qu'une fonction $f:E\to \mathbb {R} \cup \{+\infty \}$ est fortement convexe, de module $α > 0$ si, pour tous $x 1$ et $x 2$ dans $dom f$ et tout $t$ dans $[0; 1]$ , on a :

$f(t\,x_{1}+(1-t)\,x_{2})\leq t\,f(x_{1})+(1-t)\,f(x_{2})-{\frac {\alpha }{2}}\,t(1-t)\|x_{1}-x_{2}\|^{2}.$

On retrouve la notion de fonction convexe lorsque $α = 0$ .

Exemples de fonctions convexes

Voici quelques exemples de constructions de fonctions convexes :

produit d'une fonction convexe par un réel positif ;
somme de deux fonctions convexes (de plus, si $f$ est strictement convexe et $g$ est convexe alors $f + g$ est strictement convexe) ;
exponentielle d'une fonction convexe ou plus généralement, fonction composée $g\circ f$ d'une fonction réelle convexe croissante $g$ par une fonction convexe $f$ [17] ;
fonction convexe polyédrique ;
fonction d'appui d'un ensemble et plus généralement :
- fonction sous-linéaire,
- fonction conjuguée d'une fonction de E dans ℝ ;
fonction indicatrice d'un ensemble convexe ;
fonction marginale dont les valeurs sont obtenues en minimisant une seconde fonction paramétrée par ses arguments.

Voici des exemples concrets de fonctions convexes ou concaves :

les applications à la fois convexes et concaves sont les applications affines ;
une forme quadratique $x \mapsto B (x, x)$ , associée à une forme bilinéaire symétrique $B$ , est convexe si, et seulement si $B$ est positive. Elle est strictement convexe si, et seulement si $B$ est définie positive ;
la fonction log-det : $X \mapsto ln det X$ sur le convexe des matrices définies positives (dans l'espace des matrices symétriques réelles d'ordre $n$ ) est concave.

Propriétés élémentaires

Pour tout espace vectoriel topologique E de dimension infinie, il existe des fonctions convexes de domaine E qui ne sont pas continues : par exemple les formes linéaires non continues sur E.

Cependant, une proportion significative de résultats valables pour des fonctions convexes d'une variable se reproduisent à l'identique pour des fonctions convexes sur une partie d'un espace vectoriel, soit qu'on se ramène pour les prouver à considérer la restriction de la fonction à une droite, soit que la démonstration soit une simple révision de la version à une variable. En voici quelques-unes :

Une fonction convexe est une fonction dont l'épigraphe est convexe[18].
Dans un espace vectoriel topologique, une fonction qui vérifie l'inégalité de convexité pour les seuls milieux et qui est continue est convexe.
Une fonction convexe vérifie l'inégalité de Jensen.

Minorante affine

La technique de minoration des fonctions convexes par des fonctions affines est une variante adaptée à l'analyse de l'utilisation des hyperplans d'appui en géométrie convexe. La forme analytique du théorème de Hahn-Banach permettrait de minorer directement une fonction convexe définie (et à valeurs finies) sur la totalité de son espace de départ. En revanche, dès que la fonction n'est pas définie partout, il faut poser quelques restrictions techniques[19].

Proposition — Soit $E$ un espace vectoriel topologique, $f$ une fonction convexe et continue définie sur un ouvert convexe non vide $U$ de $E$ et $x 0$ un point de $U$ .

Il existe alors une fonction affine continue qui minore $f$ et qui coïncide avec elle en $x 0$ .

On verra un peu plus bas que l'hypothèse de continuité est superflue en dimension finie (c'est une conséquence de la convexité). En revanche, la condition topologique sur $U$ est indispensable, même en une seule variable : pour la fonction convexe $f(x)=-{\sqrt {1-x^{2}}}$ sur $[-1; 1]$ (dont le graphe est un demi-cercle) et $x 0 = 1$ , on ne peut trouver de fonction affine minorante au sens de la proposition précédente.

Démonstration

Considérons d'une part l'épigraphe strict $C=\{(x,y)\in U\times \mathbb {R} \,\mid \,f(x)<y\}$ de $f$ : il est convexe par convexité de $f$ , ouvert dans $E\times \mathbb {R}$ parce que $U$ est ouvert et $f$ continue, et d'autre part le singleton $L = {(x 0, f (x 0))}$ . En utilisant la première forme géométrique du théorème de Hahn-Banach, on a la garantie qu'existe un hyperplan d'appui à $C$ passant par $(x 0, f (x 0))$ , qui est fermé. Cet hyperplan ne peut contenir la droite $\{x_{0}\}\times \mathbb {R}$ car il ne contient pas $(x 0, f (x 0) + 1)$ par exemple. On en conclut qu'il est le graphe d'une application affine qui minimise $f$ , et qui est continue parce que $H$ est fermé.

Utilisation des dérivées premières

Voici un premier résultat permettant de reconnaître la convexité d'une fonction au moyen de ses dérivées premières. On note $f'(x)\in {\mathcal {L}}(E,\mathbb {R} )$ la forme linéaire continue qu'est la différentielle de $f$ au point $x$ . Le point 2 ci-dessous signifie que l'approximation affine de $f$ en tout point $x$ est une minorante de $f$ ; le point 3 exprime la monotonie de la dérivée.

Convexité et dérivées premières — Soient $E$ un espace normé, $Ω$ un ouvert convexe de $E$ et $f:\Omega \to \mathbb {R}$ une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :

$f$ est convexe sur $Ω$ ;
$\forall \,x,y\in \Omega ,\ f(y)\geq f(x)+f'(x)\cdot (y-x)$ ;
$\forall \,x,y\in \Omega ,\ (f'(y)-f'(x))\cdot (y-x)\geq 0$ .

Un résultat analogue permet de caractériser la stricte convexité d'une fonction. Il suffit de remplacer les inégalités ci-dessus par des inégalités strictes et de supposer que les points d'évaluation $x$ et $y$ diffèrent.

Stricte convexité et dérivées premières I — Soient $E$ un espace normé, $Ω$ un ouvert convexe de $E$ et $f:\Omega \to \mathbb {R}$ une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :

$f$ est strictement convexe sur $Ω$ ;
${\displaystyle \forall \,x,y\in \Omega ,\ x\neq y\$ ;
${\displaystyle \forall \,x,y\in \Omega ,\ x\neq y\$ .

En dimension finie, les inégalités ci-dessus peuvent être renforcées[20].

Stricte convexité et dérivées premières II — Soient $E$ un espace vectoriel de dimension finie, $f:E\to \mathbb {R}$ une fonction de classe C¹ et $t \in ]0; 1[$ . Alors les propriétés suivantes sont équivalentes :

$f$ est strictement convexe ;
pour tout $β >0$ , il existe une fonction $g_{\beta }:[0,2\beta ]\to \mathbb {R} _{+}$ continue, strictement croissante, vérifiant $g_{\beta }(0)=0$ et

{\displaystyle \forall x,y\in \Omega ,\ \|x\|,\|y\|\leq \beta \

;

pour tout $β >0$ , il existe une fonction $g_{\beta }:[0,2\beta ]\to \mathbb {R} _{+}$ continue, strictement croissante, vérifiant $g_{\beta }(0)=0$ et
${\displaystyle \forall x,y\in \Omega ,\ \|x\|,\|y\|\leq \beta \$ .

On peut enfin caractériser la forte convexité au moyen des dérivées premières.

Forte convexité et dérivées premières — Soient $E$ un espace euclidien, $Ω$ un ouvert convexe de $E$ et $f:\Omega \to \mathbb {R}$ une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :

$f$ est fortement convexe sur $Ω$ ;
${\displaystyle \exists \alpha >0,\forall x,y\in \Omega \$ ;
${\displaystyle \exists \alpha >0,\forall \,x,y\in \Omega \$ .

Utilisation des dérivées secondes

On note $f''(x)\in {\mathcal {L}}_{2}(E,\mathbb {R} )$ la forme bilinéaire continue et symétrique qu'est la différentielle seconde de $f$ au point $x$ .

Convexité et dérivées secondes — Soient $Ω$ un ouvert d'un espace normé et $f:\Omega \to \mathbb {R}$ une fonction deux fois différentiable.

$f$ est convexe si, et seulement si, pour tout point $x \in Ω$ , la forme bilinéaire $f'' (x)$ est positive.
Si, pour tout point $x \in Ω$ , $f''(x)$ est définie positive, alors $f$ est strictement convexe.

Rappelons que la réciproque du second point est fausse (voir supra).

Fonctions convexes en dimension finie

Continuité sur un ouvert

Comme en dimension 1, une fonction convexe définie sur un ouvert de ℝⁿ est forcément continue en tout point de l'ouvert. La démonstration va nous donner une information plus précise[21] :

Théorème — Une fonction convexe définie (et à valeurs finies) sur un ouvert de ℝⁿ est localement lipschitzienne, donc continue et dérivable presque partout.

Démonstration

Soit $f$ une fonction convexe définie sur l'ouvert convexe $C$ , et soit $x 0$ un point de $C$ .

On va dans un premier temps montrer que $f$ est localement bornée. La dimension finie est utilisée ici de façon essentielle.

Pour majorer localement $f$ , prenons un simplexe contenant $x 0$ en son intérieur, et notons $M$ la plus grande valeur prise par $f$ sur les n + 1 sommets de ce simplexe. L'inégalité de convexité permet d'étendre cette majoration à tout le simplexe, donc à un voisinage de $x 0$ .

Passons à la minoration locale, valable sur toute boule $B$ centrée en $x 0$ sur laquelle on sache déjà majorer $f$ par un $M$ . Pour tout point $x 1$ de cette boule, en introduisant le symétrique $x 1'$ de $x 1$ par rapport à $x 0$ et en écrivant l'inégalité de convexité pour $x 0$ comme milieu de $[x 1, x 1']$ et en y reportant la majoration de $f (x 1')$ , on obtient la minoration $2f(x_{0})-M\leq f(x_{1})$ .

Soit alors $δ$ un réel strictement positif assez petit pour que $f$ prenne des valeurs plus petites que $M$ (et donc plus grandes que $2 f (x 0) - M$ sur la boule ouverte $B 2$ de centre $x 0$ et de rayon $2 δ$ . On vérifie alors assez facilement que $f$ est $L$ -lipschitzienne sur la boule ouverte $B 1$ de centre $x 0$ et de rayon $δ$ , où l'on pose :

L={2(M-f(x_{0})) \over \delta }.

Pour cette vérification, soit $x 1$ et $x 2$ distincts dans $B 1$ . On introduit les points auxiliaires $x 1'$ et $x 2'$ définis par :

x_{1}'=x_{1}-\delta {{x_{2}-x_{1}} \over {\|x_{2}-x_{1}\|}}

et

x_{2}'=x_{2}+\delta {{x_{2}-x_{1}} \over {\|x_{2}-x_{1}\|}}

.

On remarque que ces points auxiliaires sont dans $B 2$ . Si l'on écrit successivement alors les inégalités de convexité correspondant à la représentation de $x 1$ comme un point du segment $[x'_{1},x_{2}]$ et à la représentation de $x 2$ comme un point du segment $[x 1, x 2']$ , puis qu'on y insère les majorations et minorations disponibles pour les valeurs de $f$ sur $B 2$ , on obtient rapidement la majoration souhaitée :

\left|f(x_{2})-f(x_{1})\right|\leq L\|x_{2}-x_{1}\|.

En dimension > 1, l'ensemble négligeable des points où $f$ n'est pas dérivable peut avoir la puissance du continu : considérer par exemple[22] l'application convexe $\mathbb {R} ^{2}\to \mathbb {R} ,\ (x,y)\mapsto \max(x,0)$ .

Discontinuités au bord

À une variable, sur un intervalle non ouvert, on a vu qu'une fonction convexe n'était pas nécessairement continue.

Néanmoins il est possible de la rendre continue par un procédé simple : si $f$ est convexe sur un intervalle $[a, b]$ , alors nécessairement la limite à droite $f + (a)$ de $f$ en $a$ existe et est inférieure ou égale à la valeur $f (a)$ . La discontinuité de $f$ en la borne $a$ se produit alors dans le cas où $f + (a) < f (a)$ . On peut s'en démêler en modifiant simplement la valeur de $f$ en ce point : il suffit de la diminuer et la remplacer par $f + (a)$ [23].

Dès la dimension 2, les choses ne sont pas aussi confortables, comme le montre l'exemple suivant :

Soit $C$ le disque-unité fermé de ℝ² ; considérons la fonction $f$ définie sur $C$ par :

\left\{{\begin{matrix}f(x,y)&=&\displaystyle {x^{2} \over {y+1}}&{\mbox{si }}(x,y)\not =(0,-1)\\f(0,-1)&=&0.&\\\end{matrix}}\right.

Cette fonction $f$ est convexe. Elle est toutefois discontinue au point $(0 , -1)$ mais ici la discontinuité ne peut être levée par une simple modification de la valeur $f (0, -1)$ . On constate en effet que si on tend radialement vers ce point, la fonction étant nulle sur le rayon, $f (0, y)$ tend vers 0 ; mais un calcul facile permet de constater que, si on tend vers $f (0, -1)$ le long du cercle frontière de C, $f (x, y)$ tend vers 2. Toutes les valeurs comprises entre 0 et 2 sont d'ailleurs valeurs d'adhérence de $f$ au point $(0, -1)$ et il est définitivement illusoire d'espérer rendre cette $f$ continue en modifiant ses valeurs sur le bord[24].

Toutefois, si l'ensemble de définition est un polytope, les choses se passent comme sur les intervalles de ℝ, comme on peut le voir en appliquant le théorème suivant[25] :

Théorème — Une fonction convexe bornée définie sur l'intérieur d'un polytope admet un prolongement convexe continu au polytope.

Fermeture d'une fonction convexe

Une fois qu'on a compris qu'il est vain de vouloir modifier une fonction convexe $f$ sur la frontière de son domaine de définition jusqu'à la rendre continue, on peut néanmoins choisir un jeu de valeurs sur cette frontière plus remarquable que les autres, en exigeant que le prolongement soit à la fois semi-continu inférieurement (ce qui nécessite de choisir des valeurs faibles) et convexe (ce qui nécessite de les prendre fortes).

Pour écrire l'énoncé assez confortablement, il est ici particulièrement approprié d'utiliser des fonctions définies sur tout ℝⁿ et prenant éventuellement la valeur $+\infty$ .

Théorème — Soit $f$ une fonction convexe de domaine effectif $\operatorname {dom} f\subset \mathbb {R} ^{n}$ . On note $f$ la fonction définie en $x\in \mathbb {R} ^{n}$ par :

${\overline {f}}(x):=\liminf _{y\to x}f(y).$

La fonction $f$ est alors caractérisée par l'une au choix des trois propriétés suivantes :

$f$ coïncide avec $f$ en les points qui ne sont pas sur la frontière relative du convexe $dom f$ ; elle est convexe et semi-continue inférieurement ;
$f$ coïncide avec $f$ en les points qui ne sont pas sur la frontière relative de $dom f$ et, pour tout point $x$ de la frontière relative de $dom f$ et tout segment semi-ouvert $] x, z]$ inclus dans l'intérieur relatif de $dom f$ , $f(x)=\lim _{\stackrel {y\to x}{y\in ]x,z]}}f(y)$ ;
$f$ a pour épigraphe l'adhérence de l'épigraphe de $f$ .

Démonstration

Le fait que $f$ est semi-continue inférieurement et la propriété (3) sont vrais sans utiliser l'hypothèse de convexité de $f$ , et sont de simples exercices de topologie élémentaire.

Le fait que $f$ coïncide avec $f$ hors de l'adhérence de $dom f$ , c'est-à-dire prenne la valeur $+\infty$ en tout point de cette partie de l'espace est lui aussi évident.

Le fait que $f$ coïncide avec $f$ sur l'intérieur relatif de $dom f$ provient de la continuité de la restriction de $f$ à cet intérieur relatif, en tant que fonction convexe sur un convexe ouvert (relativement à son enveloppe affine).

La convexité de $f$ peut sembler claire, puisque son épigraphe est convexe comme adhérence d'un convexe, mais il y a ici un piège ! Il ne faut en effet pas oublier de vérifier que $f$ prend ses valeurs dans $\mathbb {R} \cup \{+\infty \}$ (autrement dit, que la $liminf$ servant à définir $f$ ne vaut nulle part $-\infty$ ) ce qui n'est pas évident. Pour ce faire, il est souhaitable de se placer provisoirement dans l'enveloppe affine de $dom f$ . Par la proposition d'existence des fonctions affines minimisantes, on construit une forme affine sur ce sous-espace qui minore $f$ sur l'intérieur relatif de $dom f$ ; la minoration est encore vraie sur la frontière relative (on s'en aperçoit point par point en restreignant l'espace de départ à une droite passant par ce point), on prolonge enfin arbitrairement cette forme affine à ℝⁿ tout entier en une forme affine, continue puisqu'on est en dimension finie, et qui minore partout $f$ . Cette forme minore alors aussi les $liminf$ qui construisent $f$ prouvant qu'elles ne peuvent valoir $-\infty$ .

Une fois connue la convexité de $f$ , donc de sa restriction à tout segment, l'affirmation (2) provient du lemme facile suivant : une fonction d'une seule variable qui est à la fois convexe et semi-continue inférieurement est en fait continue.

Il est clair que (2) et que (3) caractérisent $f$ . Pour (1), cela découle du paragraphe précédent de la démonstration, dans lequel on a montré que (1) entraîne (2).

La fonction $f$ est appelée la fermeture de $f$ . Les fonctions convexes égales à leur fermeture sont appelées des fonctions convexes fermées ; dit autrement ce sont les fonctions convexes dont l'épigraphe est fermé, ou encore autrement dit ce sont les fonctions convexes semi-continues inférieurement[26].

Fonction à valeurs vectorielles

On peut aussi introduire une notion de convexité pour les fonctions à valeurs vectorielles, pourvu que l'on se donne un cône dans l'espace d'arrivée de la fonction.

De façon plus précise, on suppose donnés deux espaces vectoriels $E$ et $F$ , un convexe $C$ de $E$ , un cône pointé convexe $K$ de $F$ et une fonction $f$ de $C$ dans $F$ . On dit que $f$ est $K$ -convexe si, pour tous $x 1$ et $x 2$ de $C$ et tout $t$ dans $[0; 1]$ , on a

$f(tx_{1}+(1-t)x_{2})\in tf(x_{1})+(1-t)f(x_{2})-K.$

Par les propriétés supposées de $K$ , l'ensemble des fonctions $K$ -convexes est un cône convexe de l'ensemble des fonctions de $E$ dans $F$ (parce que $K$ est un cône convexe), contenant les fonctions affines (parce que $K$ est pointé).

Si le cône $K$ est également saillant, il induit sur $f$ un ordre partiel, noté $\leq K$ et défini par

$y_{1}\leq _{K}y_{2}\qquad \Longleftrightarrow \qquad y_{2}-y_{1}\in K.$

Alors, l'expression ci-dessus de la $K$ -convexité de $f$ s'écrit aussi

$f(tx_{1}+(1-t)x_{2})\leq _{K}tf(x_{1})+(1-t)f(x_{2}),$

ce qui rappelle l'inégalité de convexité familière.

Applications en physique

L'analyse convexe trouve un grand nombre d'applications en physique, lorsque les potentiels énergétiques sont localement convexes (existence de solutions stables, de changements de phase). En homogénéisation, par exemple, les théories de type variationnel permettent d'estimer les solutions d'équations aux dérivées partielles elliptiques grâce à la représentation des potentiels énergétiques par transformée de Legendre. La transformée de Legendre, formulation mathématique qui représente une fonction convexe par l'ensemble de ses tangentes, permet le développement de méthodes de linéarisation[27].

Notes et références

Démontré p. 179 de J. L. W. V. Jensen, « Sur les fonctions convexes et les inégalités entre les valeurs moyennes », Acta Mathematica, vol. 30,‎ 1906, p. 175-193 (DOI 10.1007/BF02418571, lire en ligne).
(en) Emil Artin, The Gamma Function, Dover, 2015 (1^re éd. 1964), 48 p. (lire en ligne), p. 5.
Une hypothèse de ce type est indispensable, car toutes les solutions $f$ de l'équation fonctionnelle de Cauchy satisfont $f\left({\frac {x_{1}+x_{2}}{2}}\right)={\frac {f(x_{1})+f(x_{2})}{2}}$ .
Ce résultat est attribué à Jensen par (en) Constantin Nicolescu et Lars-Erik Persson (en), Convex Functions and their Applications : A Contemporary Approach, Springer, coll. « Ouvrages de mathématiques de la Société mathématique du Canada » (n^o 23), 2006 (ISBN 978-0-387-24300-9, lire en ligne), p. 10. Ils renvoient à Jensen 1906, qui démontre directement une inégalité plus générale (voir infra).
Artin 2015, p. 6. Pour une autre méthode, voir Nicolescu et Persson 2006, ou la Propriété 11 de la leçon « Fonctions convexes » sur Wikiversité.
Démonstration de l'inégalité de Jensen dans la leçon « Fonctions convexes » sur Wikiversité.
Jensen 1906, p. 180, repris dans Artin 2015, p. 6.
Ce résultat est cité par Nicolescu et Persson 2006, p. 20-21, qui l'attribuent à L. Galvani, renvoyant à son article « Sulle funzioni convesse di una o due variabili, definite in un aggregato qualunque », Rend. Circ. Mat. Palermo, vol. 41, 1916, p. 103-134 DOI:10.1007/BF03018290.
On trouve une démonstration dans Artin 2015, p. 1 et 6, ou dans le chapitre « Convexité » de la leçon sur les fonctions d'une variable réelle sur Wikiversité.
Voir Nicolescu et Persson 2006, p. 21, qui attribuent les deux premiers points à Otto Stolz, renvoyant à son traité Grundzüge der Differential und Integralrechnung, vol. 1, Teubner, Leipzig, 1893.
Cf. Propriété 13 et Théorème 1 de la leçon « Fonctions convexes » sur Wikiversité.
Énoncé dans Jacques Douchet, Analyse : recueil d'exercices et aide-mémoire, vol. 1, PPUR, 2010, 3^e éd. (1^re éd. 2003) (lire en ligne), p. 77 (prop. 5.44) et démontré dans cet exercice corrigé de la leçon sur les fonctions d'une variable réelle sur Wikiversité. Pour une généralisation aux fonctions convexes d'une variable vectorielle, voir (en) Jean-Paul Penot, Calculus Without Derivatives, coll. « GTM » (n^o 266), 2012 (lire en ligne), p. 202-203.
Cf. Théorème 2 de la leçon « Fonctions convexes » sur Wikiversité.
(en) Stephen Boyd et Lieven Vandenberghe, Convex Optimization, Cambridge University Press, 2004 (lire en ligne), p. 110.
Pour l'ensemble de cette sous-section, voir (en) Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, coll. « Grundlehren Text Editions », 2004 (1^re éd. 2001), 259 p. (ISBN 978-3-540-42205-1, lire en ligne), p. 74-76.
Selon ce qu'en dit R. T. Rockafellar dans le CIM Bulletin.
Cf. Propriétés 8 et 9 de la leçon « Fonctions convexes » sur Wikiversité.
(en) Werner Fenchel, Convex Cones, Sets, and Functions, Princeton University Press, 1951 (lire en ligne), p. 57.
La proposition qui suit est énoncée dans Nicolescu et Persson 2006, p. 114 (sous l'hypothèse d'un espace $E$ normé, qui ne joue pas un rôle essentiel dans la preuve).
R. Glowinski, J.-L. Lions et R. Trémolières, Analyse numérique des inéquations variationnelles, t. 1 : Théorie Générale, Premières Applications, Paris, Dunod-Bordas, 1976, p. 61 et 63, Lemmes 1.1 et 1.2.
Hiriart-Urruty et Lemaréchal 2004, p. 102-104, la minoration de la fonction convexe ayant été adaptée au vu de Nicolescu et Persson 2006, p. 119.
Nicolescu et Persson 2006, p. 137.
Ces remarques sont disponibles, avec leurs preuves et quelques détails, dans Nicolescu et Persson 2006, p. 22.
L'exemple figure dans Hiriart-Urruty et Lemaréchal 2004, p. 105, avec l'explication de la convexité de $f$ .
Ce théorème est cité sans démonstration par Nicolescu et Persson 2006, p. 123, qui renvoient à (en) D. Gale, V. Klee et R. T. Rockafellar, « Convex functions on convex polytopes », Proc. Amer. Math. Soc., vol. 19,‎ 1968, p. 867-873.
Pour l'ensemble de cette sous-sous-section, voir Hiriart-Urruty et Lemaréchal 2004, p. 79-80. Nicolescu et Persson 2006, p. 122, mentionnent également ces résultats en les attribuant à Fenchel 1951.
Voir pour un aperçu (en) Ivar Ekeland et Roger Temam, Convex Analysis and Variational Problems, SIAM, 1999, 402 p. (ISBN 978-0-89871-450-0, lire en ligne), chap. IV.

Voir aussi

Articles connexes

Bibliographie

(en) R. Tyrrell Rockafellar, Convex Analysis, Princeton, Princeton University Press, 1970, 451 p. (ISBN 978-0-691-01586-6, lire en ligne)

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Démontré p. 179 de J. L. W. V. Jensen, « Sur les fonctions convexes et les inégalités entre les valeurs moyennes », Acta Mathematica, vol. 30,‎ 1906, p. 175-193 (DOI 10.1007/BF02418571, lire en ligne).

[2] (en) Emil Artin, The Gamma Function, Dover, 2015 (1^re éd. 1964), 48 p. (lire en ligne), p. 5.

[3] Une hypothèse de ce type est indispensable, car toutes les solutions $f$ de l'équation fonctionnelle de Cauchy satisfont $f\left({\frac {x_{1}+x_{2}}{2}}\right)={\frac {f(x_{1})+f(x_{2})}{2}}$ .

[4] Ce résultat est attribué à Jensen par (en) Constantin Nicolescu et Lars-Erik Persson (en), Convex Functions and their Applications : A Contemporary Approach, Springer, coll. « Ouvrages de mathématiques de la Société mathématique du Canada » (n^o 23), 2006 (ISBN 978-0-387-24300-9, lire en ligne), p. 10. Ils renvoient à Jensen 1906, qui démontre directement une inégalité plus générale (voir infra).

[5] Artin 2015, p. 6. Pour une autre méthode, voir Nicolescu et Persson 2006, ou la Propriété 11 de la leçon « Fonctions convexes » sur Wikiversité.

[6] Démonstration de l'inégalité de Jensen dans la leçon « Fonctions convexes » sur Wikiversité.

[7] Jensen 1906, p. 180, repris dans Artin 2015, p. 6.

[8] Ce résultat est cité par Nicolescu et Persson 2006, p. 20-21, qui l'attribuent à L. Galvani, renvoyant à son article « Sulle funzioni convesse di una o due variabili, definite in un aggregato qualunque », Rend. Circ. Mat. Palermo, vol. 41, 1916, p. 103-134 DOI:10.1007/BF03018290.

[9] On trouve une démonstration dans Artin 2015, p. 1 et 6, ou dans le chapitre « Convexité » de la leçon sur les fonctions d'une variable réelle sur Wikiversité.

[10] Voir Nicolescu et Persson 2006, p. 21, qui attribuent les deux premiers points à Otto Stolz, renvoyant à son traité Grundzüge der Differential und Integralrechnung, vol. 1, Teubner, Leipzig, 1893.

[11] Cf. Propriété 13 et Théorème 1 de la leçon « Fonctions convexes » sur Wikiversité.

[12] Énoncé dans Jacques Douchet, Analyse : recueil d'exercices et aide-mémoire, vol. 1, PPUR, 2010, 3^e éd. (1^re éd. 2003) (lire en ligne), p. 77 (prop. 5.44) et démontré dans cet exercice corrigé de la leçon sur les fonctions d'une variable réelle sur Wikiversité. Pour une généralisation aux fonctions convexes d'une variable vectorielle, voir (en) Jean-Paul Penot, Calculus Without Derivatives, coll. « GTM » (n^o 266), 2012 (lire en ligne), p. 202-203.

[13] Cf. Théorème 2 de la leçon « Fonctions convexes » sur Wikiversité.

[14] (en) Stephen Boyd et Lieven Vandenberghe, Convex Optimization, Cambridge University Press, 2004 (lire en ligne), p. 110.

[15] Pour l'ensemble de cette sous-section, voir (en) Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, coll. « Grundlehren Text Editions », 2004 (1^re éd. 2001), 259 p. (ISBN 978-3-540-42205-1, lire en ligne), p. 74-76.

[16] Selon ce qu'en dit R. T. Rockafellar dans le CIM Bulletin.

[17] Cf. Propriétés 8 et 9 de la leçon « Fonctions convexes » sur Wikiversité.

[18] (en) Werner Fenchel, Convex Cones, Sets, and Functions, Princeton University Press, 1951 (lire en ligne), p. 57.

[19] La proposition qui suit est énoncée dans Nicolescu et Persson 2006, p. 114 (sous l'hypothèse d'un espace $E$ normé, qui ne joue pas un rôle essentiel dans la preuve).

[20] R. Glowinski, J.-L. Lions et R. Trémolières, Analyse numérique des inéquations variationnelles, t. 1 : Théorie Générale, Premières Applications, Paris, Dunod-Bordas, 1976, p. 61 et 63, Lemmes 1.1 et 1.2.

[21] Hiriart-Urruty et Lemaréchal 2004, p. 102-104, la minoration de la fonction convexe ayant été adaptée au vu de Nicolescu et Persson 2006, p. 119.

[22] Nicolescu et Persson 2006, p. 137.

[23] Ces remarques sont disponibles, avec leurs preuves et quelques détails, dans Nicolescu et Persson 2006, p. 22.

[24] L'exemple figure dans Hiriart-Urruty et Lemaréchal 2004, p. 105, avec l'explication de la convexité de $f$ .

[25] Ce théorème est cité sans démonstration par Nicolescu et Persson 2006, p. 123, qui renvoient à (en) D. Gale, V. Klee et R. T. Rockafellar, « Convex functions on convex polytopes », Proc. Amer. Math. Soc., vol. 19,‎ 1968, p. 867-873.

[26] Pour l'ensemble de cette sous-sous-section, voir Hiriart-Urruty et Lemaréchal 2004, p. 79-80. Nicolescu et Persson 2006, p. 122, mentionnent également ces résultats en les attribuant à Fenchel 1951.

[27] Voir pour un aperçu (en) Ivar Ekeland et Roger Temam, Convex Analysis and Variational Problems, SIAM, 1999, 402 p. (ISBN 978-0-89871-450-0, lire en ligne), chap. IV.