Recombinaison (cosmologie)
En cosmologie, la recombinaison, souvent qualifiée de Grande recombinaison, désigne la formation des atomes neutres par association des électrons et des noyaux atomiques, précédemment indépendants les uns des autres[alpha 1]. Ce phénomène se produit au moment où la température de l'Univers descend en dessous du seuil sous lequel l'énergie moyenne des photons les plus énergétiques est en dessous de l'énergie d'ionisation de l'atome considéré. À l'époque de la recombinaison, les seuls noyaux atomiques présents dans l'Univers sont l'hydrogène, l'hélium et des traces de lithium. Le lithium se recombine (partiellement) avant l'hélium, lui-même se recombinant avant l'hydrogène.


En pratique, quand on parle de recombinaison, on évoque implicitement celle de l'hydrogène uniquement, qui représente la grande majorité des noyaux existant à cette époque. Cet événement se situe environ 380 000 ans après le Big Bang. Il est à l'origine du fond diffus cosmologique.
Selon certains auteurs, la recombinaison marque la fin de l'époque de l'univers primordial[3],[4]. Elle correspond au moment où les structures de l'univers actuel (étoiles, galaxies, amas de galaxies, etc.) se mettent en place, après le découplage du rayonnement[3],[5].
Chronologie
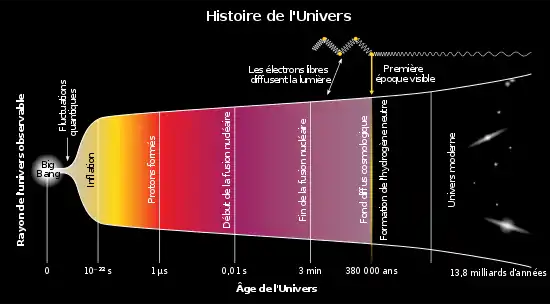
Avant les recombinaisons, l'Univers ne possède pas d'atomes neutres. La formation de ces derniers débute par l'association des nucléons (protons et neutrons) en noyaux atomiques lors de la nucléosynthèse primordiale, qui se serait produite durant les premières minutes après le Big Bang. Après cette nucléosynthèse, environ le quart de la masse de la matière (8 % des noyaux) est sous forme de noyaux d'hélium (2 protons et 2 neutrons) alors que les trois-quarts restant (92 % des noyaux) sont des protons libres[6],[7]. Il y a également d'infimes quantités de noyaux de deutérium (un proton et un neutron), de tritium (un proton et deux neutrons) et de lithium 7 (3 protons et 4 neutrons) qui se forment à cette époque[8],[9]. Les neutrons qui ne sont pas intégrés à des noyaux se désintègrent en protons et électrons[10].
À cette époque, les électrons circulent librement dans l'Univers et forment alors la principale source d'interaction entre matière et lumière, par l'intermédiaire de la diffusion Thomson[11],[12]. L'Univers est alors opaque au rayonnement : les photons sont diffusés par les électrons libres selon un processus semblable à celui du brouillard[13],[14]. Ainsi, le libre parcours moyen des photons est très faible : ils sont diffusés par la « brume d'électrons »[1] libres.
Les temps auxquels se déroulent les différents événements sont exprimés en termes de décalage vers le rouge, noté z (z augmente indéfiniment quand on remonte vers le Big Bang). Notamment, 1 100 correspond à 380 000 ans après le Big Bang (aBB), et 6 à 800 millions d'années aBB[15]. La température de l'Univers décroît en suivant la relation approximative[15],[alpha 2] T (MeV) 1√[t (s)].
Recombinaisons du lithium et de l'hélium
| Ion | Énergie (eV[alpha 3]) |
|---|---|
| Li3+ → Li2+ | 122,4 |
| Li2+ → Li+ | 75,6 |
| He2+ → He+ | 54,4 |
| He+ → He0 | 24,6 |
| H+ → H0 | 13,6 |
| Li+ → Li0 | 5,4[alpha 4] |
La baisse de température de l'Univers engendre la recombinaison par ordre décroissant d'énergie. Cela amène d'abord la recombinaison des atomes de lithium et d'hélium[17], en passant par des niveaux d'ionisation intermédiaires pour redescendre jusqu'à l'état neutre (hélium) ou monoionisé (lithium). Chaque recombinaison s'accompagne d'une émission de rayonnement () correspondant à l'énergie d'ionisation impliquée (tableau ci-contre).
Les premières recombinaisons sont celles du lithium (). D'abord de l'état triplement ionisé à doublement ionisé, puis de doublement ionisé à simplement ionisé[15] :
- , vers 14 000 ;
- , vers 8 600.
Ensuite se produisent celles de l'hélium (), d'abord de l'état doublement ionisé à simplement ionisé, puis de simplement ionisé à l'état neutre[15] :
- , vers 6 000 ;
- , vers 2 500.
La première suit l'équation de Saha et se serait produite à un décalage vers le rouge (z) d'environ 6 000[20]. Ainsi, la moitié de l'hélium simplement ionisé aurait été formé à partir de z = 5 800[18]. La seconde recombinaison ne suivrait pas l'équation de Saha et se serait produite un peu plus tard, pour atteindre 90 % vers z ~ 2 000[21],[18].
Recombinaison de l'hydrogène
Selon le modèle standard de la cosmologie et les observations du télescope spatial Planck, on estime que la recombinaison de l'hydrogène se produit environ 380 000 ans après le Big Bang. À ce moment, la température moyenne de l'Univers passe sous les 3 000 K, ce qui fait en sorte que son énergie n'est plus suffisante pour maintenir séparés les protons (ou deutons) et les électrons libres qui n'ont pas précédemment formé les atomes de lithium et d'hélium lors de la recombinaison de ces derniers[22]. Ces protons (ou deutons) et ces électrons se combinent alors pour former de l'hydrogène neutre (deutérium compris), monoatomique[15] :
- , vers 1 300.
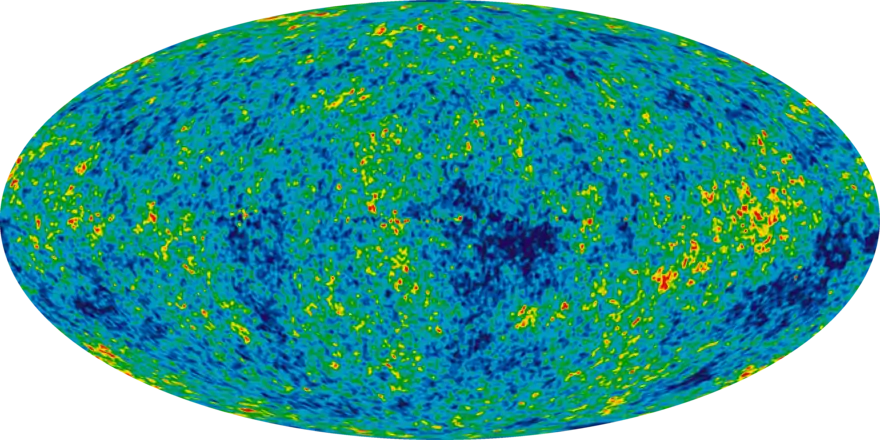
Cette recombinaison diminue drastiquement la densité d'électrons libres qui diffusaient jusqu'alors les photons (seul 2/10 000e des électrons ne se recombinent pas[17]). Ainsi, après la recombinaison de l'hydrogène, la presque totalité de la matière devient neutre et il n'y a à peu près plus d'électrons libres diffusant les photons. Certaines longueurs d'onde associées au spectre de l'hydrogène sont absorbées, mais l'effet est négligeable[23]. Cela entraîne le découplage du rayonnement et l'émission du FDC.
On remarque que le lithium n'atteint pas la neutralité (la recombinaison ne se produit pas), en raison des photons de la raie Lyman α émis lors de la recombinaison de l'hydrogène[19] (qui réionisent les atomes neutres de lithium éventuellement recombinés), et aussi en raison de la diminution drastique (de cinq ordres de grandeur) de l'abondance des électrons[15].
Bien que la recombinaison de l'hydrogène ne se soit pas produite instantanément, elle se serait produite suffisamment rapidement pour que l'on considère que l'émission du FDC provient d'une « surface », appelée surface de dernière diffusion, d'épaisseur négligeable[13].
Premières réactions chimiques
| Espèce | Abondance, rapportée au nombre d'atomes H |
|---|---|
| H2 | 6,3 × 10−7 |
| H− | 1,8 × 10−13 |
| H+ 2 | 9,2 × 10−15 |
| H+ 3 | 8,0 × 10−17 |
| H− 3 | 5,5 × 10−33 |
| HD | 4,2 × 10−10 |
| HD+ | 1,2 × 10−18 |
| D+ | 6,1 × 10−19 |
| H2D+ | 1,6 × 10−20 |
| HeH+ | 1,7 × 10−14 |
| He+ | 9,8 × 10−23 |
| He+ 2 | 9,3 × 10−36 |
| Li+ | 4,3 × 10−10 |
| Li | 8,0 × 10−12 |
| LiH | 9,0 × 10−20 |
| LiH+ | 4,6 × 10−20 |
| Li− | 1,7 × 10−22 |
| LiHe+ | 3,0 × 10−23 |
La chimie primitive de l'Univers concerne la période comprise entre la fin de la recombinaison de l'hélium vers 2 000, et la réionisation du gaz intergalactique qui commence vers 15 et se termine vers 6 ( 800 Ma aBB). Pour la décrypter il faut prendre en compte environ 250 réactions chimiques potentielles[24]. Non pas que le nombre d'espèces chimiques impliquant H, He et Li soit très grand (environ 30), mais il faut prendre en compte les différents états vibrationnels de chacune. Les principales étapes sont les suivantes[15] :
2 000 ≲ z ≲ 800
À 1 000 la fraction d'hydrogène ionisé est encore de l'ordre de 10 %, à 800 elle n'est plus que de 1 %. Pendant cette période une (petite) partie des atomes d'hélium (neutres) réagissent avec les protons résiduels :
Cette première réaction chimique, qui produit le premier composé chimique de l'Univers, est rapidement suivie de la formation d'hydrogène diatomique, ionisé ou non :
où l'un des atomes d'hydrogène peut être du deutérium (production conjointe de et ).
Tandis que les abondances de H2 et HD augmentent continûment, celles de H+
2, HD et HeH+ passent par un maximum puis diminuent jusqu'à un minimum vers z ≈ 800.
Formalisme
Équation de Saha
La recombinaison des atomes peut d'abord être estimée à l'aide de l'équation de Saha :
où :
- est la densité des atomes dans leur i-ème état d'ionisation, c'est-à-dire avec i électrons arrachés
- est la densité d'électrons,
- est le niveau de dégradation énergétique des états pour les ions i-ème,
- est l'énergie d'ionisation,
- est la longueur d'onde thermique de de Broglie d'un électron[alpha 5],
- est la température du gaz, en kelvins (K),
- est la constante de Boltzmann.
Pour l'hydrogène, cela donne[16] :
où :
- est la masse d'un électron.
- est l'énergie d'ionisation de l'hydrogène, soit 13,6 électron-volt (eV),
- est le nombre d'atomes d'hydrogène neutre
Intuitivement, on serait tenté de dire que la recombinaison se produit quand l'énergie « moyenne » des photons est de l'ordre de l'énergie d'ionisation de l'atome d'hydrogène, soit 13,6 eV, ou environ 150 000 K[16]. En pratique, cette estimation est très incorrecte, car l'Univers est un système qui a un nombre considérable de photons par noyau atomique (de l'ordre de grandeur du milliard pour un)[25]. De ce fait, ce qui importe est que l'énergie du milliardième des photons les plus énergétiques soit de l'ordre de l'énergie d'ionisation de l'atome d'hydrogène. Ceci se produit quand l'énergie moyenne de « l'ensemble » des photons est bien inférieure à 13,6 eV.
Pour déterminer cette énergie, il faut d'abord déterminer le rapport entre le nombre d'électrons libres () et le nombre de noyau d'hydrogène et d'atomes d'hydrogène ()[16] :
Si l'on considère que la nucléosynthèse primordiale est responsable de 76 % de la quantité d'hydrogène, l'équation de Saha devient[16],[alpha 6] :
où :
- est la densité baryonique,
- est la constante de Planck.
Si l'on combine cette équation et l'évaluation du facteur par WMAP, on obtient une énergie moyenne d'environ 0,3 eV, pour une température de 3 000 K. À ce moment, estimé de nos jours à 380 000 ans après le Big Bang, on calcule qu'il reste environ 1 % d'atomes d'hydrogène ionisé[26],[27].
Toujours selon l'équation de Saha, les recombinaisons de l'hélium s'écrivent[28] :
et
Cela donne la moitié de l'hélium recombiné à l'état fondamental pour z = 2500[28].
Ces approches constituent une estimation supposant que la recombinaison se produit à l'équilibre thermique, ce qui ne serait pas tout à fait le cas.
Modèle de Peebles
En 1968, les physiciens Jim Peebles[29] et Yakov Borisovich Zel'dovich et al.[30] établissent indépendamment une approche de la recombinaison sans supposer que cette dernière se produit à l'équilibre thermique. Les principaux points de leurs modèles s'énoncent ainsi :
- Les recombinaisons directes jusqu'à l'état fondamental de l'hydrogène sont peu efficaces. Elles mènent à l'émission d'un photon dont l'énergie est plus grande que 13,6 eV, qui réionise un atome voisin.
- Les électrons se recombinent conséquemment à des états excités et descendent rapidement chacun des niveaux vers le premier état excité n = 2.
- À partir de cet état, les électrons peuvent atteindre l'état fondamental n = 1 selon deux parcours :
- Les atomes du premier état excité peuvent être réionisés par les photons du FDC avant d'atteindre l'état fondamental. Pour tenir compte de cela, Peebles définit un facteur qui est la probabilité qu'un atome atteigne l'état fondamental par l'un des deux processus précédent avant d'être réionisé.
Selon ces modèles, la recombinaison s'écrit sous la forme de l'équation différentielle suivante :
où :
- est le coefficient de recombinaison du « case B »,
- est le taux de photoionisation correspondant,
- est l'énergie du premier état excité = 10,2 eV.
Cela mène à une recombinaison beaucoup plus lente que celle prévue par l'équation de Saha.
| Élément | % recombiné | z | |
|---|---|---|---|
| Peebles | Saha | ||
| Hydrogène | 50 | 1210 | 1370 |
| 90 | 980 | 1250 | |
| 99 | 820 | 1140 | |
| Hélium | 50 | 2000 | 2500 |
| 90 | 1830 | ||
Développements ultérieurs
Le modèle de Peebles tient compte des principes physiques les plus importants. Cependant, on y retrouve encore des approximations menant à des erreurs de l'ordre de 10 %. Puisque la recombinaison est d'une importance cruciale pour l'analyse des anisotropies du FDC[32], plusieurs groupes de recherche ont peaufiné le modèle au cours des dernières décennies.
Les modèles actuels seraient précis à environ 0,1 % et certains sont en libre accès[33].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Recombination (cosmology) » (voir la liste des auteurs).
Notes
- Le terme de recombinaison est quelque peu impropre, puisque c'est en fait la première fois qu'électrons et noyaux se sont combinés. Le terme recombinaison provient du fait que ce phénomène a d'abord été étudié au laboratoire, où il s'agissait bien de la recombinaison en atomes neutres d'un gaz préalablement ionisé[2].
- Quand on parle d'une température exprimée en MeV il s'agit en fait de où désigne la constante de Boltzmann : 1 MeV = 11,605 × 109 K.
- Les niveaux d'énergie sont donnés en ordre décroissant puisque la température de l'Univers diminue avec le temps. Cela implique que la recombinaison des niveaux d'ionisation les plus énergétiques s'effectue avant celle des plus basses énergies.
- Cette combinaison ne se serait pas produite en raison de l'émission Ly α engendrée par la recombinaison de l'hydrogène[19]. Ainsi, le lithium primordial serait encore simplement ionisé.
- , où est la constante de Planck et la masse d'un électron.
- Hirata a construit cette équation en considérant la température en unités de 104 K. Dans le présent article, l'équation a été modifiée pour éliminer ce facteur.
Références
- Séguin et Villeneuve 2002, p. 383
- « Glossaire », sur http://www.cnrs.fr, (consulté le )
- Lachièze-Rey 2013, p. 81
- Lachièze-Rey et Gunzig 1995, p. 18.
- Reeves 1994, p. 201.
- « Formations des élements légers », sur https//media4.obspm.fr, Observatoire de Paris (consulté le )
- (en) Bludman, S. A., « Baryonic Mass Fraction in Rich Clusters and the Total Mass Density in the Cosmos », The Astrophysical Journal, vol. 508, no 2, , p. 535–538 (DOI 10.1086/306412, Bibcode 1998ApJ...508..535B, arXiv astro-ph/9706047)
- (en) Graig J. Hogan, « Primordial Deuterium and the Big Bang », sur http://www.indiana.edu (consulté le )
- Reeves 1994, p. 180-182.
- Séguin et Villeneuve 2002, p. 386
- Hirata 2008, p. 3.
-
- « Le fond diffus cosmologique (CMB) », sur http://www.apc.univ-paris7.fr, APC - AstroParticule et Cosmologie, (consulté le )
- Luminet 2001, p. 353
- Séguin et Villeneuve 2002, p. 382.
- (en) Daniele Galli et Francesco Palla, « The Dawn of Chemistry », Annual Review of Astronomy and Astrophysics, vol. 51, , p. 163-206 (DOI 10.1146/annurev-astro-082812-141029, arXiv 1211.3319v1).
- Hirata 2008, p. 4
- Hirata 2008, p. 10
- Hirata 2008, p. 11
- Hirata 2008, p. 12
- (en) E. R. Switzer et C. M. Hirata, « Primordial helium recombination. III. Thomson scattering, isotope shifts, and cumulative results », Physical Review D, vol. 77, no 8, (lire en ligne)
- (en) E. R. Switzer & C. M. Hirata, « Primordial helium recombination. I. Feedback, line transfer, and continuum opacity », Physical Review D, vol. 77, no 8, (lire en ligne)
- Reeves 1994, p. 127-128.
- Séguin et Villeneuve 2002, p. 158.
- (en) C. D. Gay, P. C. Stancil, S. Lepp et A. Dalgarno, « The Highly Deuterated Chemistry of the Early Universe », The Astrophysical Journal, vol. 737, no 1, , p. 44- (DOI 10.1088/0004-637X/737/1/44).
- Reeves 1994, p. 138-139.
- Lachièze-Rey 2013, p. 82.
- Reeves 1994, p. 138.
- Hirata 2008, p. 10-11
- (en) P. J. E. Peebles, « Recombination of the Primeval Plasma », Astrophysical Journal, vol. 153, , p. 1 (DOI 10.1086/149628, Bibcode 1968ApJ...153....1P)
- (en) Y. B. Zeldovich, V. G. Kurt et R. A. Syunyaev, « Recombination of Hydrogen in the Hot Model of the Universe », Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki, vol. 55, , p. 278 (Bibcode 1968ZhETF..55..278Z)
- (en) H. Nussbaumer et W. Schmutz, « The hydrogenic 2s-1s two-photon emission », Astronomy and Astrophysics, vol. 138, no 2, , p. 495
- (en) W. Hu, D. Scott, N. Sugiyama et M. White, « Effect of physical assumptions on the calculation of microwave background anisotropies », Physical Review D, vol. 52, no 10, , p. 5498
- (en) « CosmoRec », sur UToronto.ca
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) Christopher Hirata, Physics 217bc : The Standard Model - Cosmology. : lecture 6, Caltech, (lire en ligne), « 3 Hydrogen recombination – equilibrium theory », p. 1-16.

- (en) Marc Lachièze-Rey, Initiation à la Cosmologie, Dunod, , 5e éd., 176 p. (ISBN 978-2-10-059240-1, lire en ligne), chap. 4.2.1 (« Découplage et recombinaison »), p. 81–83.

- (en) Marc Lachièze-Rey et E. Gunzig, Le Rayonnement cosmologique : Trace de l'Univers primordial, Paris/Milan/Barcelone, Masson, , 216 p. (ISBN 2-225-84924-2, ISSN 1164-5962).

- Jean-Pierre Luminet, L'Univers chiffonné, Paris, Gallimard, coll. « Folio essais », (réimpr. 2005), 487 p. (ISBN 2-07-030052-8).

- Hubert Reeves, Dernières nouvelles du cosmos : Vers la première seconde, Paris, Éditions du Seuil, , 237 p. (ISBN 2-02-020571-8 et 2-02-022831-9).

- Marc Séguin et Benoît Villeneuve, Astronomie et astrophysique, Éditions du Renouveau Pédagogique, , 2e éd., 618 p. (ISBN 978-2-7613-1184-7, présentation en ligne).

Articles connexes
- Équation de Saha
- Équations de Friedmann
- Fond diffus cosmologique
- Découplage du rayonnement
- Réionisation
- Portail de la cosmologie