Règle du palier de Maxwell
En thermodynamique, la règle du palier de Maxwell, ou construction de Maxwell, permet, à partir d'une équation d'état représentant à la fois les états liquide et gazeux d'un corps pur, de calculer la pression de vapeur saturante à laquelle s'effectue la transition de phase entre les deux états à une température donnée.
Cette règle a été établie par le physicien James Clerk Maxwell qui la publia en 1875[1]. Le raisonnement originel de Maxwell est basé sur les courbes isothermes produites par l'équation d'état de van der Waals, établie en 1873. Elle peut se démontrer rigoureusement indépendamment de l'équation d'état choisie pour faire le calcul.
Problématique
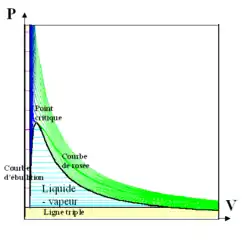
Ces isothermes expérimentales permettent entre autres d'observer la transition critique et le palier de pression au changement de phase liquide-gaz.

En rouge l'isotherme critique. Au-dessus (courbes vertes) le fluide est supercritique. Au-dessous (courbes bleues) le fluide peut être liquide ou gazeux.
Dans les années 1860, le chimiste et physicien irlandais Andrews mesura expérimentalement la pression et le volume de nombreux corps (notamment du dioxyde de carbone) en fonction de la température. Il traça pour chacun de ces corps des courbes isothermes dans un diagramme de Clapeyron ou diagramme P-V, voir figure 1. Ces courbes sont appelées isothermes d'Andrews ou plus simplement isothermes. Andrews fut l'un des premiers à observer le point critique. Les courbes isothermes montrent également des paliers de pression dans le changement d'état liquide-gaz (lignes horizontales bleu turquoise de la figure 1, le changement de phase se faisant à pression constante pour une température donnée).
Avant l'apparition de l'équation d'état de van der Waals (1873), aucune équation d'état n'était en mesure de représenter les isothermes d'Andrews. Si l'on dispose d'une équation d'état analytique de type équation d'état cubique, comme l'équation d'état de van der Waals, permettant de calculer explicitement la pression en fonction des variables d'état volume et température et permettant de représenter les deux phases liquide et gaz, on peut tracer des séries de courbes isothermes dans un diagramme P-V, comme sur la figure 2.
On constate qu'il existe une courbe critique (en rouge sur la figure 2) au-dessus de laquelle, à des températures élevées, les isothermes (en vert sur la figure 2) sont décroissantes de façon monotone et n'associent qu'un seul volume à une pression donnée : le fluide est supercritique. En dessous de cette température critique, toute isotherme présente une plage de pression dans laquelle une pression est associée à trois volumes (points L, J et G des courbes isothermes bleu turquoise de la figure 2) : une phase gaz et une phase liquide peuvent exister ; en dehors de cette plage de pression l'isotherme est monotone décroissante : le corps pur n'existe que dans une seule phase, liquide ou gaz.
L'équation d'état représente donc qualitativement le comportement d'un fluide par la transition critique et par la possibilité de transition liquide-gaz. Elle n'est toutefois pas exacte puisque selon elle la transition gaz-liquide pourrait s'effectuer sur une certaine plage de pression (entre la pression du point I et celle du point K des isothermes bleu turquoise de la figure 2) pour une température donnée, alors que l'expérience montre qu'à une température donnée il n'existe pour un corps pur qu'une seule pression de vapeur saturante.
La règle du palier de Maxwell (1875) permet de calculer cette pression de vapeur saturante à partir de l'équation d'état. Il faudra attendre 1901 et l'introduction de la notion de fugacité par Lewis[2] pour qu'une démonstration rigoureuse de cette règle soit donnée.
Énoncé de la règle
La règle de Maxwell indique la position du palier LG d'une isotherme correspondant à la pression de vapeur saturante du corps pur à cette température.
Dans le diagramme P-V, pour une isotherme donnée, soit un cycle isotherme (théorique) partant du point L (représentant un liquide saturé), parcourant l'isotherme selon la courbe LIJKG jusqu'au point G (représentant un gaz saturé) et revenant par le palier isobare GL. Le palier isobare représente le changement d'état gaz-liquide réel à température constante : le cycle est donc intégralement effectué à température constante. D'après le deuxième principe de la thermodynamique, énoncé de Thomson sur la non-existence du moteur monotherme (un cycle monotherme ne peut fournir du travail), à supposer le cycle réversible, alors le travail fourni par le cycle ne peut être que nul :
- .
Ce raisonnement n'est pas rigoureux car sur une partie de l'isotherme (entre les points I et K de l'isotherme bleu turquoise de la figure 2) , ce qui implique que la compressibilité du fluide est négative et que le cycle passe par un état instable de la matière. Un tel cycle ne saurait donc exister. Néanmoins la règle peut se démontrer rigoureusement par l'égalité des potentiels chimiques des deux phases à l'équilibre, ce que nous verrons plus bas.

On note :
- la température ;
- la pression de vapeur saturante à ;
- le volume du liquide à et , c'est-à-dire au point L de la figure 2 ;
- le volume du gaz à et , c'est-à-dire au point G de la figure 2.
On calcule :
- , le travail fourni par le cycle lors de l'aller par la courbe isotherme LIJKG,
- , le travail fourni par le cycle au retour par le palier isobare GL.
Le travail produit par le cycle est donc égal à :
d'où l'expression de la règle du palier de Maxwell :
| Règle du palier de Maxwell : à saturation |
ou encore :
D'un point de vue graphique, cette règle revient à dire que la pression de vapeur saturante de l'isotherme se situe sur le palier pour lequel les deux aires, positives, des deux surfaces violettes de la figure 3 sont égales.
Démonstration
La variation isotherme du potentiel chimique en fonction de la pression vaut :
avec :
- la pression ;
- la température ;
- le volume ;
- le potentiel chimique ;
- la quantité de matière, ou nombre de moles ;
- le volume molaire : .
Intégrons cette expression à température et quantité de matière constantes entre les deux points L (liquide saturé) et G (gaz saturé) :
L'équilibre des phases à pression et température données est caractérisé par l'égalité des potentiels chimiques des deux phases :
on a donc :
En intégrant par parties on obtient :
Les points L et G étant à la même pression , on retrouve l'expression de la règle du palier de Maxwell[2] :
On remarquera que cette démonstration rigoureuse est indépendante de l'équation d'état qui sera employée lors du calcul, alors que Maxwell a basé sa démonstration sur la forme irréaliste des isothermes produites par l'équation d'état cubique de van der Waals.
Pour une expression en fonction du volume, il suffit de considérer que l'intégration est effectuée à quantité de matière constante, d'où :
ainsi, en multipliant l'expression obtenue précédemment par :
Application avec l'équation d'état de van der Waals
On peut effectuer complètement les calculs avec l'équation d'état de van der Waals (ou toute autre équation d'état permettant de représenter le liquide et le gaz, comme les équations d'état cubiques). La température étant donnée, on a un système de trois inconnues (les volumes molaires et et la pression ) et trois équations :
- l'équation d'état appliquée à la phase gaz :
- l'équation d'état appliquée à la phase liquide :
- l'équation issue de la règle du palier de Maxwell :
Le calcul de la pression de vapeur saturante d'un corps pur à température donnée , la température critique, peut être effectué de manière itérative :
- fixer la pression , la pression critique,
- calculer la ou les racines de la forme cubique de l'équation d'état de van der Waals à et ,
- si l'équation d'état de van der Waals ne produit qu'une seule racine réelle, recommencer en 1,
- si l'équation d'état de van der Waals produit trois racines réelles, calculer à partir de la plus grande et à partir de la plus petite,
- calculer avec l'équation d'état de van der Waals,
- si recommencer en 1,
- sinon .
Exemple - Pression de vapeur saturante de l'azote[3].
- Pour l'azote on dispose des données suivantes :
- = 0,133 Pa m6 mol−2 ;
- = 3,744 × 10−5 m3 mol−1.
- Pour une température de 100 K on calcule :
- = 0,575 09 × 10−4 m3 mol−1 ;
- = 0,136 79 × 10−3 m3 mol−1 ;
- = 1,28 MPa.
- La littérature donne une pression de vapeur saturante expérimentale de l'azote à 100 K égale à 0,76 MPa. Ceci illustre les défauts de l'équation de van der Waals, bien que la règle du palier de Maxwell soit exacte.
Notes et références
Notes
- (en) Maxwell, J. C., « On the Dynamical Evidence of the Molecular Constitution of Bodies. », Nature, vol. 11, , p. 357–359 (DOI 10.1038/011357a0, Bibcode 1875Natur..11..357C).
- (en) Gilbert Newton Lewis, « The Law of Physico-Chemical Change », Proceedings of the American Academy of Arts and Sciences, vol. 37, no 3, , p. 49–69 (DOI 10.2307/20021635).
- (en) Jochen Vogt, Exam Survival Guide : Physical Chemistry, Springer, , 382 p. (ISBN 9783319498102, lire en ligne), p. 26-29.
Bibliographie
- Bernard Claudel, Propriétés thermodynamiques des fluides, vol. B 8020, Techniques de l'ingénieur, , p. 1-46.
- Jean-Pierre Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1026, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et cinétique chimique, pack Opérations unitaires. Génie de la réaction chimique, univers Procédés chimie - bio - agro », , p. 1-30.
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique : + de 6500 termes, nombreuses références historiques, des milliers de références bibliographiques, Louvain-la-Neuve, De Boeck supérieur, , 976 p. (ISBN 978-2-8073-0744-5, lire en ligne), p. 153-154.
- Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », , 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne), p. 103.
Liens externes
- L’équation d’état de Van der Waals, Patrick Eggli, Laboratoire de Recherche et de Chimie Bienne, .
- Cours Second Bachelier - Thermodynamique - Chapitre 7 : Changement d’état, Nicolas Vandewalle, GRASP | Soft Matter | Université de Liège.
Voir aussi
- Équation d'état de van der Waals
- Fugacité
- Potentiel chimique
- Pression de vapeur saturante
- Transition de phase
- Portail de la physique
- Portail de la chimie