Fugacité
En chimie physique, et plus particulièrement en thermodynamique, la fugacité d'une espèce chimique exprime l'écart entre les propriétés de cette espèce pure ou dans un mélange réel et les propriétés de cette même espèce à l'état de gaz parfait pur. La notion de fugacité est applicable à toutes les phases (gaz, liquide, solide), elle permet notamment le calcul des équilibres de phases.
À la suite de l'apparition de l'équation d'état de van der Waals en 1873, il devenait possible de calculer les équilibres de phases gaz-liquide. En effet, cette équation novatrice pour son époque permettait de calculer aussi bien les propriétés d'un gaz que celles d'un liquide. Willard Gibbs et Pierre Duhem introduisirent peu après (1875 à 1878) la notion de potentiel chimique, notion importante dans les équilibres de phases et les équilibres chimiques. Toutefois, la notion de potentiel chimique se révéla difficile à manipuler, car un potentiel chimique ne peut être calculé qu'à une constante additive près et non de façon absolue. De plus le potentiel chimique de toute espèce tend vers moins l'infini à dilution infinie. En 1900[1] et 1901[2], Gilbert Lewis introduisit la notion de fugacité qui décrit l'écart de comportement d'un corps réel, pur ou en mélange, par rapport au même corps à l'état de gaz parfait pur. À partir de la fugacité, Lewis introduisit en 1923[3] la notion d'activité chimique plus spécialement employée pour les phases condensées (liquide ou solide).
Les coefficients de fugacité sont calculés avec des équations d'état, ils sont également en théorie applicables à toutes les phases, mais dans la pratique leur usage est généralement restreint aux gaz ; les phases liquide et solide sont le plus souvent représentées par des activités chimiques.
Définitions
Fugacité
La variation isotherme à composition constante du potentiel chimique d'un corps pur ou en mélange en fonction de la pression est donnée par la relation :
avec le volume molaire du corps pur ou le volume molaire partiel du corps en mélange.
Pour un gaz parfait pur, le volume molaire vaut :
En conséquence, la variation isotherme du potentiel chimique d'un gaz parfait pur vaut :
Lewis s'inspira de cette relation pour introduire la notion de fugacité d'un corps , notée , qu'il définit ainsi[3] :
| Variation isotherme du potentiel chimique : |
La fugacité a la dimension d'une pression.
La fugacité d'un gaz parfait pur est égale à la pression : . La fugacité d'un corps dans un mélange de gaz parfaits est égale à la pression partielle de ce corps : , avec la fraction molaire du corps dans le mélange. Ces deux relations ne sont pas vraies pour un corps réel.
La fugacité se définit pour n'importe quelle phase, aussi bien pour un gaz que pour un liquide, un solide ou un fluide supercritique. Elle se définit également aussi bien pour un état réel que pour un état théorique : gaz parfait comme vu précédemment ou tout autre état standard.
L'intégration, à température et pression constantes, de l'expression définissant la fugacité donne la relation entre le potentiel chimique du corps dans un mélange réel et le potentiel chimique du même corps à l'état de gaz parfait pur aux mêmes pression et température que le mélange réel :
Cette expression donne une autre définition de la fugacité, toutes les grandeurs étant définies aux mêmes pression et température, mais pas nécessairement aux mêmes composition (fractions molaires ) et état :
| Fugacité : |
avec :
- la pression du mélange réel ;
- la température du mélange réel ;
- la fugacité du corps dans le mélange réel ;
- le potentiel chimique du corps dans le mélange réel ;
- le potentiel chimique du corps à l'état de gaz parfait pur aux mêmes et que le mélange réel ;
- la constante universelle des gaz parfaits.
Coefficient de fugacité
Le théorème de Gibbs conduit à la relation suivante :
entre le potentiel chimique du corps à l'état de gaz parfait pur et le potentiel chimique du même corps dans un mélange de gaz parfaits, les deux potentiels étant définis aux mêmes pression et température, étant la fraction molaire du corps dans le mélange. Nous avons donc, en utilisant la définition de la fugacité, la relation :
dans laquelle les deux potentiels chimiques sont définis aux mêmes pression, température et composition. Cette relation montre que la fugacité d'un corps dans un mélange de gaz parfaits est égale à la pression partielle de ce corps :
Pour tout corps du mélange, le rapport entre la fugacité réelle et la fugacité du gaz parfait en mélange aux mêmes pression, température et composition est appelé coefficient de fugacité, il est noté :
| Coefficient de fugacité : |
Le coefficient de fugacité est adimensionnel.
Le coefficient de fugacité exprime l'écart entre le potentiel chimique d'un corps dans un mélange réel et le potentiel chimique de ce même corps en mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel :
Le coefficient de fugacité exprime également l'écart entre le potentiel chimique d'un corps dans un mélange réel et le potentiel chimique de ce même corps à l'état de gaz parfait pur, aux mêmes pression et température :
Par définition, le coefficient de fugacité d'un gaz parfait en mélange est donc égal à 1 :
À fortiori pour un gaz parfait pur :
Le gaz parfait correspond au cas idéal dans lequel les molécules n'ont aucune interaction entre elles hormis des chocs élastiques.
Lorsque les molécules s'attirent, la pression réelle est inférieure à celle du gaz parfait correspondant de même composition, à la même température et dans le même volume : dans ce cas et .
Inversement, lorsque les molécules se repoussent, la pression réelle est supérieure à celle du gaz parfait correspondant de même composition, à la même température et dans le même volume : dans ce cas et .
Enthalpie libre résiduelle
Une grandeur résiduelle exprime l'écart entre une grandeur thermodynamique extensive d'un mélange réel (gaz, liquide ou solide) et la même grandeur thermodynamique extensive d'un mélange de gaz parfaits aux mêmes pression, température et composition :
Les relations suivantes sont également vraies entre grandeurs molaires et grandeurs molaires partielles, respectivement réelles, du gaz parfait et résiduelles :
Pour l'enthalpie libre , l'identité des potentiels chimiques et des enthalpies libres molaires partielles permet d'écrire :
Le deuxième terme est donc l'enthalpie libre molaire partielle résiduelle :
Le théorème d'Euler sur les fonctions homogènes du premier ordre s'applique aux grandeurs résiduelles puisque ce sont des grandeurs extensives. Avec nombre de moles et fraction molaire de chacun des corps présents dans le mélange, on a donc en particulier pour l'enthalpie libre :
Calcul de la fugacité et du coefficient de fugacité
Dépendance à la pression
Le potentiel chimique varie de façon isotherme selon :
et par définition, de façon isotherme également, selon :
On peut donc écrire directement[4] :
avec le volume molaire partiel du corps dans le mélange.
En intégrant entre les pressions de référence et du mélange, on obtient :
soit :
avec la fugacité dans l'état de référence à la pression et la température du mélange. Le terme exponentiel est appelé facteur ou correction de Poynting :
Dépendance à la température
Le potentiel chimique varie de façon isobare selon :
En prenant un état de référence à la même température que le mélange réel, on écrit :
avec le potentiel chimique du corps dans l'état de référence. Puisque l'on a, par intégration de la relation définissant la fugacité :
on obtient[4] :
avec :
- la fugacité du corps dans l'état de référence à la même température que le mélange ;
- l'enthalpie molaire partielle du corps dans le mélange ;
- l'enthalpie molaire partielle du corps dans l'état de référence à la même température que le mélange.
En prenant comme référence l'état de gaz parfait pur aux mêmes pression et température que le mélange réel, la fugacité de référence est égale à la pression, soit . La dérivée partielle s'effectuant à pression constante, on obtient :
avec l'enthalpie molaire du corps à l'état de gaz parfait pur à la température du mélange (un gaz parfait répondant à la deuxième loi de Joule, son enthalpie ne dépend pas de la pression).
Dépendance à la composition
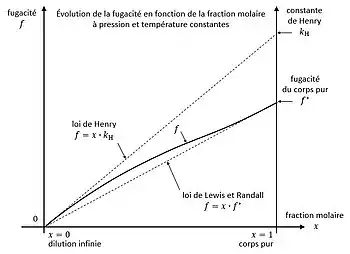
À pression et température constantes, la fugacité possède deux limites, avec la fraction molaire du corps dans le mélange :
- à dilution infinie : ;
- pour le corps pur : ;
avec la fugacité du corps pur. En vertu de la règle de L'Hôpital, on définit la constante de Henry par :
L'évolution de la fugacité en fonction de la composition est encadrée par deux lois[5],[6] :
Dans un mélange de composants, la relation de Gibbs-Duhem impose pour tout composant du mélange[4] :
avec la quantité du corps dans le mélange. D'autre part, le théorème de Schwarz appliqué à l'enthalpie libre donne, pour deux corps et quelconques du mélange :
et par conséquent la relation sur les fugacités :
On peut donc écrire, à partir de la relation de Gibbs-Duhem :
Formules générales
Quelles que soient les conditions de pression et de température, la fugacité d'un gaz est calculée à l'aide du coefficient de fugacité :
Pour un liquide, le calcul de la fugacité d'un composant est effectué à l'aide du coefficient de fugacité pour les hautes pressions (plus de 10 atm), ou pour des pressions proches de la pression critique du composant. Pour les basses pressions, le calcul est effectué à l'aide d'un coefficient d'activité selon l'approche symétrique pour un solvant et selon l'approche dissymétrique pour un gaz dissout (dont la température critique est inférieure à la température du mélange liquide). Le tableau suivant résume le calcul de la fugacité en phase liquide.
| Solvant | Gaz dissout | |
|---|---|---|
| 10 atm ou |
||
| 10 atm | ||
avec :
- la température d'équilibre ;
- la pression d'équilibre ;
- la pression de vapeur saturante du corps pur à ;
- la pression à laquelle la constante de Henry a été expérimentalement déterminée à ;
- la constante de Henry du corps à et dans le solvant ;
- la fraction molaire du corps en phase vapeur ;
- la fraction molaire du corps en phase liquide ;
- la coefficient de fugacité du corps en phase vapeur, à , et composition du mélange gazeux ;
- le coefficient de fugacité du corps pur à saturation en phase vapeur, à et ;
- le coefficient d'activité du corps en phase liquide, à , et composition du mélange liquide ;
- le coefficient d'activité du corps en phase liquide, à , et dilution infinie dans le solvant ;
- le volume molaire liquide du corps pur à ;
- le volume molaire partiel du corps en phase liquide, à , et dilution infinie dans le solvant ;
- la correction de Poynting pour un solvant ;
- la correction de Poynting pour un soluté.
Cas des gaz parfaits et des solutions liquides idéales
Un gaz se comportant comme un gaz parfait aux hautes températures et aux basses pressions (moins de 10 atm), la fugacité d'un gaz dans un mélange dans ces conditions peut être assimilée à sa pression partielle :
En phase liquide, si celle-ci se comporte comme une solution idéale, la fugacité peut être calculée selon :
Étant donné l'égalité des fugacités dans les équilibres de phases (voir chapitre Équilibre de phases), on retrouve ainsi, dans les conditions d'idéalité, la loi de Raoult :
et la loi de Henry :
Calcul du coefficient de fugacité
Contrairement au potentiel chimique qui n'est toujours défini qu'à une constante additive près, le coefficient de fugacité peut être calculé de façon absolue, ce qui le rend particulièrement intéressant dans le calcul des propriétés des mélanges réels. Si ce calcul est en théorie possible pour toutes les phases (gaz, liquide, solide), il est en pratique utilisé pour les phases gazeuses à toutes les pressions et pour les phases liquides aux hautes pressions (plus de 10 atm) : il nécessite en effet une équation d'état, or il n'en existe pas à l'heure actuelle représentant convenablement les phases condensées, du moins à basse pression (moins de 10 atm).
Avec une équation d'état explicite en pression
Avec une équation d'état dans laquelle la pression est exprimée explicitement en fonction du volume , de la température et de la composition (nombre de moles de chacun des constituants du mélange), , telle que les équations d'état cubiques de van der Waals, Soave-Redlich-Kwong, Peng-Robinson, le coefficient de fugacité du corps se calcule selon :
ou, sous forme adimensionnelle :
avec :
- la dérivée partielle de la pression par rapport à la quantité du corps , à volume, température et quantités des corps autres que constants ;
- le nombre de moles du corps dans le mélange ;
- le nombre de moles total dans le mélange ;
- le volume molaire du mélange réel ;
- le facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le volume molaire valant , le facteur de compressibilité est constant , d'où et le coefficient de fugacité .
Soit un mélange de constituants à pression , température et volume , chaque constituant étant représenté par moles, le mélange étant en une seule phase (gaz, liquide ou solide).
Le coefficient de fugacité de tout constituant est défini par la relation :
Pour le mélange réel, le potentiel chimique peut indifféremment s'écrire en fonction des variables réelles :
Pour le mélange de gaz parfaits correspondant il n'en va pas de même, car à , et composition du mélange réel le volume correspondant est calculé selon :
d'où la relation :
La variation isotherme du potentiel chimique de tout constituant en fonction du volume est donnée par :
En intégrant cette relation entre un volume quelconque et le volume du mélange, à température et composition constantes, on obtient :
Pour un mélange de gaz parfaits en particulier, pour tout corps , on a :
d'où les relations entre potentiels chimiques du constituant à l'état de gaz parfait :
Dans cette dernière relation on identifie :
avec le volume molaire du mélange réel et le facteur de compressibilité du mélange réel.
Nous pouvons écrire :
Lorsque le volume tend vers l'infini (lorsque la pression tend vers 0), le comportement du mélange réel à température et composition (nombre de moles) constantes tend vers celui du mélange de gaz parfaits, aussi peut-on écrire :
d'où :
or par définition :
d'où :
En divisant les expressions par (il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par :
Étant donné que la dérivée partielle de la pression est considérée à volume et température constants, on peut écrire :
Avec la quantité de matière totale dans le mélange, et , on a :
d'où :
Avec une équation d'état explicite en volume
Avec une équation d'état dans laquelle le volume est exprimé explicitement en fonction de la pression , de la température et de la composition (nombre de moles de chacun des constituants du mélange), , comme l'une des formes de l'équation du viriel, le coefficient de fugacité du corps se calcule selon :
ou, sous forme adimensionnelle :
avec :
- le volume molaire partiel du corps dans le mélange réel ;
- le nombre de moles du corps dans le mélange ;
- le nombre de moles total dans le mélange ;
- le volume molaire du mélange réel ;
- le facteur de compressibilité du mélange réel.
On vérifie que pour un gaz parfait, le volume molaire valant , le facteur de compressibilité est constant , d'où et le coefficient de fugacité .
Soit un mélange de constituants à pression , température et volume , chaque constituant étant représenté par moles, le mélange étant en une seule phase (gaz, liquide ou solide).
La variation isotherme du potentiel chimique de tout constituant en fonction de la pression est donnée par :
avec le volume molaire partiel du constituant :
En intégrant cette relation entre une pression quelconque et la pression du mélange, à température et composition constantes, on obtient :
Pour un mélange de gaz parfaits en particulier, le volume molaire partiel de tout corps vaut :
d'où la relation entre potentiels chimiques du constituant à l'état de gaz parfait :
En soustrayant l'expression obtenue pour les gaz parfaits à l'expression générale obtenue précédemment, nous avons :
Lorsque la pression tend vers 0, le comportement du mélange réel à température et composition constantes tend vers celui du mélange de gaz parfaits, aussi peut-on écrire :
d'où :
or par définition :
d'où :
En divisant les expressions par (il est possible de l'extraire de l'intégrale puisque la température est constante dans toutes les expressions) et dans l'intégrale en factorisant par :
Étant donné que la dérivée partielle du volume est considérée à pression et température constantes, on peut écrire :
Avec la quantité de matière totale dans le mélange, et , on a :
d'où :
Selon le type d'équation d'état utilisé, il existe donc deux formules couramment utilisées pour le calcul du coefficient de fugacité :
- avec une équation d'état explicite en pression : ,
- avec une équation d'état explicite en volume : .
Le coefficient de fugacité lie les propriétés d'un mélange réel à celles d'un gaz parfait aux mêmes pression, température et composition. Son calcul implique le passage par un état intermédiaire dans lequel le mélange réel se comporte comme un gaz parfait. Soient moles d'un mélange réel à pression et température dans un volume ; la phase de ce mélange est indifférente, il peut s'agir d'un gaz, d'un liquide ou d'un solide. En conservant constantes la température et la quantité de matière, ce mélange réel se comporte comme un gaz parfait à pression nulle et donc à volume infini (les molécules étant infiniment éloignées les unes des autres elles n'ont plus d'interaction entre elles, ce qui définit le gaz parfait) ; dans cet état intermédiaire, le produit pression volume vaut .
La première expression du coefficient du fugacité donne :
En utilisant la relation :
on obtient :
La différentielle de la pression :
donne à température et composition constantes :
et par conséquent, en considérant le changement de variable et les bornes d'intégration liées à l'état réel pour la borne supérieure et à l'état intermédiaire pour la borne inférieure :
D'autre part, le produit pression volume valant pour le mélange réel et pour l'état intermédiaire :
avec :
donne, en considérant les bornes relatives aux états réel (borne supérieure) et intermédiaire (borne inférieure) :
On a donc l'égalité des deux relations :
Équilibre de phases
Relation générale
Lorsque deux phases ou plus (gaz, liquide, solide) sont en équilibre, les potentiels chimiques de chacun des corps en présence sont homogènes sur l'ensemble des phases. Autrement dit, s'il existe à l'équilibre les phases , les potentiels chimiques de tout corps présent répondent à l'égalité :
En introduisant les fugacités respectives de tout corps dans chacune de ces phases, on peut écrire pour chacun des potentiels chimiques :
Le potentiel chimique du corps pur à l'état de gaz parfait est le même dans toutes ces expressions, puisque la pression et la température sont les mêmes dans toutes les phases à l'équilibre. L'égalité des potentiels chimiques du corps dans l'ensemble des phases à l'équilibre conduit à la condition d'équilibre des phases :
| Condition d'équilibre des phases : |
En termes de condition d'équilibre des phases, l'égalité des fugacités est tout à fait équivalente à l'égalité des potentiels chimiques : si l'une est vérifiée, l'autre est aussi vérifiée, et réciproquement. Néanmoins, les potentiels chimiques ne pouvant être déterminés qu'à une constante additive près, l'égalité des potentiels chimiques est difficilement utilisable, tandis que les fugacités peuvent être déterminées de façon absolue, ce qui les rend particulièrement utiles.
Les équilibre de phases sont le plus souvent calculées selon deux approches : l'approche (phi-phi) et l'approche (gamma-phi). L'approche nécessite deux modèles distincts : une équation d'état pour la phase vapeur et un modèle de coefficient d'activité pour la phase liquide ; elle est recommandée pour des pressions inférieures à 10 bar. Au-delà, l'approche est recommandée car elle ne nécessite qu'une seule et même équation d'état pour représenter les deux phases, ce qui rend le calcul cohérent à l'approche du point critique où les deux phases doivent se rejoindre. Les deux modèles de l'approche posent des problèmes de convergence numérique autour du point critique.
Approche ϕ - ϕ
Dans un équilibre liquide-vapeur, les fugacités des deux phases et peuvent être calculées à partir d'une même équation d'état (par exemple l'équation d'état cubique de Soave-Redlich-Kwong ou Peng-Robinson) : cette approche est alors appelée « approche » (phi-phi). En introduisant les fractions molaires respectives et les coefficients de fugacité respectifs de tout corps dans chacune des phases à l'équilibre, on peut écrire pour chacune des fugacités :
L'égalité des fugacités du corps dans l'ensemble des phases à l'équilibre conduit à l'expression de l'approche (phi-phi) :
| Approche : |
On déduit également de cette expression le coefficient de partage, noté , du corps entre les phases et :
On peut de même établir des coefficients de partage entre toutes les autres phases.
Pour un corps pur à saturation, c'est-à-dire en équilibre liquide-vapeur avec , on note et les coefficients de fugacité dans les deux phases : l'approche conduit à l'égalité , soit également à . Avec les expressions données dans le paragraphe Calcul du coefficient de fugacité on obtient par réarrangement l'expression de la règle du palier de Maxwell[2].
Approche γ - ϕ
Comme évoqué plus haut, il n'existe pas à l'heure actuelle d'équation d'état représentant convenablement les phases liquides, notamment aux basses pressions (moins de 10 atm) : il est alors préférable pour calculer les fugacités des phases liquides d'employer un modèle de coefficient d'activité et l'approche dite « approche » (gamma-phi) pour le calcul de l'équilibre de phases.
Pour la phase vapeur, en introduisant le coefficient de fugacité en phase vapeur, l'expression de la fugacité en phase vapeur est :
Pour la phase liquide, en introduisant le coefficient d'activité en phase liquide et la fugacité du corps pur en phase liquide, l'expression de la fugacité en phase liquide est :
L'égalité des fugacités à l'équilibre des phases induit l'expression de l'approche (gamma-phi) :
| Approche : |
On déduit également de cette expression le coefficient de partage du corps entre les deux phases, noté :
Cette approche est développée dans l'article Activité chimique. Elle conduit, pour des solutions idéales :
- à la loi de Raoult par la convention symétrique ;
- à la loi de Henry par la convention dissymétrique.
Notes
- (en)Gilbert Newton Lewis, « A New Conception of Thermal Pressure and a Theory of Solutions », Proceedings of the American Academy of Arts and Sciences, vol. 36, no 9, , p. 145-168 (DOI 10.2307/20020988).
- (en)Gilbert Newton Lewis, « The Law of Physico-Chemical Change », Proceedings of the American Academy of Arts and Sciences, vol. 37, no 3, , p. 49–69 (DOI 10.2307/20021635).
- Gilbert Newton Lewis et Merle Randall, « Thermodynamics and the free energy of chemical substances », McGraw-Hill Book Company Inc. (1923).
- Vidal 1997, p. 156.
- (en) J. P. O'Connell et J. M. Haile, Thermodynamics : Fundamentals for Applications, Cambridge University Press, (ISBN 978-1-139-44317-3, lire en ligne), p. 435.
- Jean-Pierre-Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1 026, Éditions techniques de l'ingénieur, (lire en ligne), p. 25-26.
Voir aussi
Articles connexes
Publications
- La thermodynamique des solutions, E. Darmois, J. Phys. Radium 4, 7 (1943) 129-142.
- Christophe Coquelet et Dominique Richon, « Propriétés thermodynamiques - Détermination pour les fluides purs », Techniques de l'ingénieur, base documentaire : Thermodynamique et énergétique, pack : Physique énergétique, univers : Énergies, BE 8030, pp. 1-8, 2007.
- Christophe Coquelet et Dominique Richon, « Propriétés thermodynamiques - Détermination pour les mélanges », Techniques de l'ingénieur, base documentaire : Thermodynamique et énergétique, pack : Physique énergétique, univers : Énergies, BE 8031, pp. 1-12, 2007.
- Jean-Pierre Corriou, « Thermodynamique chimique - Définitions et relations fondamentales », Techniques de l'ingénieur, base documentaire : Thermodynamique et cinétique chimique, pack : Opérations unitaires. Génie de la réaction chimique, univers : Procédés chimie - bio - agro, J 1025, pp. 1-19, 1984.
- Jean-Pierre Corriou, « Thermodynamique chimique - Diagrammes thermodynamiques », Techniques de l'ingénieur, base documentaire : Thermodynamique et cinétique chimique, pack : Opérations unitaires. Génie de la réaction chimique, univers : Procédés chimie - bio - agro, J 1026, pp. 1-30, 1985
- Robert C. Reid, John M. Prausnitz et Bruce E. Poling, « The properties of gases and liquids », Mc Graw Hill, 4 éd., 1987 (ISBN 978-0070517998).
- Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », , 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne).
- Portail de la chimie
- Portail de la physique