Problème du voyageur de commerce

En informatique, le problème du voyageur de commerce, ou problème du commis voyageur[1], est un problème d'optimisation qui consiste à déterminer, étant donné une liste de villes et les distances entre toutes les paires de villes[2], le plus court circuit qui passe par chaque ville une et une seule fois.

Le problème de voyageur de commerce : calculer un plus court circuit qui passe une et une seule fois par toutes les villes (ici 15 villes).

Malgré la simplicité de l’énoncé, on ne connaît pas d'algorithme permettant de trouver une solution exacte rapidement dans tous les cas. Plus précisément, on ne connaît pas d'algorithme en temps polynomial, et la version décisionnelle du problème du voyageur de commerce (pour une distance D, existe-t-il un chemin plus court que D passant par toutes les villes et qui termine dans la ville de départ ?) est un problème NP-complet, ce qui est un indice de sa difficulté.

C'est un problème algorithmique célèbre, qui a donné lieu à de nombreuses recherches et qui est souvent utilisé comme introduction à l'algorithmique ou à la théorie de la complexité. Il présente de nombreuses applications, que ce soit en planification, en logistique ou dans des domaines plus éloignés, comme la génétique (en remplaçant les villes par des gènes et la distance par la similarité).

Description du problème

L'énoncé du problème du voyageur de commerce est le suivant : étant donné n points (des « villes ») et les distances séparant chaque point, trouver un chemin de longueur totale minimale qui passe exactement une fois par chaque point et revienne au point de départ. Formellement, une instance est un graphe complet $G=(V,A,\omega )$ avec $V$ un ensemble de sommets, $A$ un ensemble d'arêtes et $\omega$ une fonction de coût sur les arcs. Le problème est de trouver le plus court cycle hamiltonien dans le graphe G.

Exemple

On considère la liste des villes A, B, C, D et les distances données par le dessin ci-dessous à gauche. Un premier chemin qui part de A, revient en A et qui visite toutes les villes est ABDCA. Un chemin plus court est ACBDA. Ce dernier est optimal.

Instance du problème du voyageur de commerce.

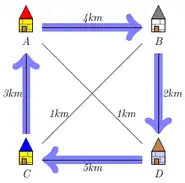Le chemin ABDCA de longueur 4+2+5+3 = 14 km.

Le chemin ACBDA est le chemin le plus court qui part de A, revient A et passe par toutes les villes. Il est de longueur 3+1+2+1 = 7 km.

Explosion combinatoire

Nombre de chemins candidats en fonction du nombre de villes
Nombre de villes $n$	Nombre de chemins candidats ${\frac {1}{2}}(n-1)!$
3	1
4	3
5	12
6	60
7	360
8	2 520
9	20 160
10	181 440
15	43 589 145 600
20	6,082 × 10¹⁶
71	5,989 × 10⁹⁹

Ce problème est plus compliqué qu'il n'y paraît ; on ne connaît pas de méthode de résolution permettant d'obtenir des solutions exactes en un temps raisonnable pour de grandes instances (grand nombre de villes) du problème. Pour ces grandes instances, on devra donc souvent se contenter de solutions approchées, car on se retrouve face à une explosion combinatoire.

Pour un ensemble de $n$ points, il existe au total $n!$ chemins possibles (factorielle de $n$ ). Le point de départ ne changeant pas la longueur du chemin, on peut choisir celui-ci de façon arbitraire, on a ainsi $(n-1)!$ chemins différents. Enfin, chaque chemin pouvant être parcouru dans deux sens et les deux possibilités ayant la même longueur, on peut diviser ce nombre par deux. Par exemple, si on nomme les points, $a,b,c,d$ , les chemins abcd et dcba, cdab et badc, adcb et bcda, cbad et dabc ont tous la même longueur ; seul le point de départ et le sens de parcours changent. On a donc ${\frac {(n-1)!}{2}}$ chemins candidats à considérer[3].

Par exemple, pour 71 villes, le nombre de chemins candidats est supérieur à 5 × 10⁸⁰ qui est environ le nombre d'atomes dans l'univers connu[4].

Variantes

Orientation

Rien n'interdit au graphe donné en entrée d'être orienté. Dans ce cas, on considère qu'un chemin existe dans un sens mais pas dans l'autre (exemple : routes à sens unique).

Asymétrie

On parle parfois de problème symétrique ou asymétrique.

Problème du voyageur de commerce symétrique : Étant donnés un ensemble de $n$ nœuds et de distances pour chaque paire de nœuds, trouver un cycle de longueur minimale qui visite chaque nœud exactement une fois. Pour $i$ et $j$ deux nœuds d'une arête, la distance de $i$ à $j$ est la même que celle de $j$ à $i$ .

Problème du voyageur de commerce asymétrique : Étant donnés un ensemble de $n$ nœuds et de distances pour chaque paire de nœuds, trouver un cycle de longueur minimale qui visite chaque nœud exactement une fois. Cette fois-ci la distance entre deux nœuds $i$ et $j$ d'une arête n'est pas forcément la même qu'on aille de $i$ à $j$ ou bien de $j$ à $i$ .

Aussi, divers problèmes de recherche opérationnelle se ramènent au voyageur de commerce. Un voyageur de commerce peu scrupuleux serait intéressé par le double problème du chemin le plus court (pour son trajet réel) et du chemin le plus long (pour sa note de frais).

Résolution exacte

Complexité du problème

Le problème de décision associé au problème d'optimisation du voyageur de commerce fait partie des 21 problèmes NP-complets de Karp[5]. Papadimitriou a démontré en 1977 que le problème reste NP-dur, même si les distances sont données par des distances euclidiennes[6]. Ainsi, le problème reste NP-dur même si on supprime la condition "ne passer au plus qu'une seule fois par une ville".

Algorithmes

Une approche de résolution naïve, mais qui donne un résultat exact, est l'énumération de tous les chemins possibles par recherche exhaustive. La complexité en temps de cet algorithme est en $O(n!)$ (plus exactement ${\frac {(n-1)!}{2}}$ , ce qui devient vite impraticable même pour de petites instances. Par exemple, si le calcul d'un chemin prend une microseconde, alors le calcul de tous les chemins pour 10 points est de 181 440 microsecondes soit 0,18 seconde, mais pour 15 points, cela représente déjà 43 589 145 600 microsecondes soit un peu plus de 12 heures et pour 20 points de 6 × 10¹⁶ microsecondes soit presque deux millénaires (1 901 années). Pour 25 villes, le temps de calcul dépasse l'âge de l'Univers.

Held et Karp ont montré que la programmation dynamique permettait de résoudre le problème en $O(n^{2}2^{n})$ [7].

Les méthodes d'optimisation linéaire sont à ce jour parmi les plus efficaces pour la résolution du problème de voyageur de commerce et permettent[N 1] désormais de résoudre des problèmes de grande taille (à l'échelle d'un pays[8]), moyennant éventuellement un temps de calcul important.

Tournée bitonique dans un graphe euclidien

Dans le cas d'un graphe euclidien, c'est-à-dire lorsque les arêtes ont pour poids les distances entre les $n$ sommets comme c'est par exemple le cas entre des villes sur une carte routière, certaines variantes du problème du voyageur de commerce ont une solution exacte qui peut être déterminée en temps polynomial. C'est le cas lorsque l'on cherche le circuit bitonique le plus rapide, où l'on part du point le plus à l'ouest pour aller toujours vers l'est jusqu'au point le plus à l'est avant de revenir au point de départ en allant toujours vers l'ouest. Dans ce cas particulier introduit pour la première fois par Jon Louis Bentley, une solution optimale peut être déterminée en $O(n^{2})$ par programmation dynamique[9].

Approximation

Cas général

Dans le cas général, et en supposant ${\mathtt {P}}\neq {\mathtt {NP}}$ , il n'existe pas d'algorithme d'approximation pour résoudre le problème du voyageur de commerce[10]. Pour le montrer on procède par l'absurde en supposant que pour un certain $\epsilon >0$ il existe un algorithme d'approximation de facteur $1+\epsilon$ . On montre alors que cet algorithme d'approximation permet de résoudre le problème de la recherche de cycle hamiltonien en temps polynomial alors même que celui-ci est NP-complet[10].

On considère un graphe $G$ , on peut supposer sans perte de généralité que toutes ses arêtes sont de poids 1. On le transforme en le graphe complet $G'$ en ajoutant à $G$ entre chaque paire de sommets non connectés une arête de poids $|S|(1+\epsilon )+1$ où $|S|$ est le nombre de sommets de $G$ . Si le graphe $G$ possède un circuit hamiltonien, alors $G'$ possède une tournée minimale de poids $|S|$ , sinon la tournée minimale contient au moins une arête de poids $|S|(1+\epsilon )+1$ et son poids vaut donc au moins $|S|(1+\epsilon )+1+|S|-1=|S|(2+\epsilon )$ . Dans le premier cas, notre algorithme d'approximation trouvera en temps polynomial une tournée de poids au plus $|S|(1+\epsilon )$ , dans l'autre il trouvera une tournée de poids au moins $|S|(2+\epsilon )>|S|(1+\epsilon )$ . Comme on peut discriminer entre les deux situations en temps polynomial, il s'ensuit que l'existence d'un circuit hamiltonien peut s'effectuer en temps polynomial ce qui aboutit à une contradiction ; il n'existe donc pas d'algorithme générique d'approximation pour résoudre le problème du voyageur de commerce.

Cas métrique

Dans certains cas, des algorithmes d'approximation existent, l'algorithme de Christofides est une approximation de facteur 3/2 dans le cas métrique, c'est-à-dire lorsque le poids des arêtes respecte l'inégalité triangulaire[11]. Dans ce cas, le problème est APX-difficile même avec des poids 1 ou 2[12]. La meilleure borne inférieure pour le facteur d'approximation est 123/122[13].

Un preprint de 2020 améliore le facteur de 3/2 - 10^-36[14]^,[15].

Cas euclidien

Dans le cas d'une métrique euclidienne, il existe un schéma d'approximation en temps polynomial. Il a été découvert indépendamment par Sanjeev Arora[16] et Joseph S. B. Mitchell[17], et leur a valu le prix Gödel en 2010[18].

Formulation par optimisation linéaire

La formalisation du problème qui suit, sous forme d'optimisation linéaire en nombres entiers du problème, est utilisée pour la conception d'algorithmes d'approximation. On note $\delta (S)$ l'ensemble des arêtes sortant de l'ensemble de sommets S.

{\begin{aligned}&{\text{minimiser}}&&\sum \mathbf {c} _{e}\mathbf {x} _{e}\\&{\text{tel que}}&&\mathbf {x(\delta (S))} \geq 2,{\text{ pour tout sous-ensemble }}\mathbf {S} {\text{ de }}\mathbf {V} ,\\&{\text{et}}&&\mathbf {x(\delta (v))} \geq 2,{\text{ pour tout élément }}\mathbf {v} {\text{ de }}\mathbf {V} ,\\&{\text{et}}&&\mathbf {x_{e}} {\text{ dans }}\mathbf {0,1} \\\end{aligned}}

La relaxation de ce programme pour un problème d'optimisation linéaire (c'est-à-dire sans les contraintes d'intégralité) est appelée relaxation de Held et Karp[19] ou subtour LP. Cette relaxation a un nombre exponentiel de contraintes, mais peut être résolue en temps polynomial en résolvant le problème de séparation, qui se révèle être le calcul d'une coupe minimum[20].

Il est conjecturé que la relaxation de Held et Karp a un trou d'intégralité (integrality gap) de 4/3[19].

Approximation de facteur 2 utilisant des arbres couvrants

L'algorithme de Christofides est basé sur un algorithme simple d'approximation de facteur 2 qui utilise la notion d'arbre couvrant de poids minimal[10]. Comme toute tournée a un poids cumulé supérieur à celui de l'arbre couvrant minimal[10] et comme un parcours préfixe de l'arbre passe deux fois par chacun des nœuds internes une tournée qui suit un parcours préfixe a un poids cumulé inférieur au double de la solution minimale au problème du voyageur de commerce[10]. Il reste à convertir ce parcours en un parcours qui passe une fois et une seule par chacun des sommets du graphe. On exploite alors l'inégalité triangulaire : si entre deux sommets le parcours considéré fait passer par un sommet intermédiaire déjà visité, on le saute pour passer directement au premier sommet non encore visité[10]. L'inégalité triangulaire assure alors que le poids total du trajet n'augmente pas ; par conséquent on obtient un circuit hamiltonien dont le poids est inférieur au double de celui du circuit minimal[10].

Heuristiques

De fait de la complexité initiale du problème ( $O(n!)$ ), de son importance, et de sa NP-completude, de nombreuses heuristiques ont été proposées.

Heuristiques de recherche locale

Une heuristique classique, appelée 2-opt est une recherche locale qui consiste à partir d'une solution et à essayer de l'améliorer en échangeant itérativement les sommets de deux arêtes. L'heuristique de Lin-Kernighan en est une amélioration[21].

Une autre heuristique de recherche locale appelée Ruiner et recréer, proche du recuit simulé, consiste à partir d'une solution, de ruiner une région de celle-ci puis de la recréer en l'améliorant[22].

Méta-heuristiques

Les algorithmes génétiques peuvent aussi être adaptés au problème du voyageur de commerce. L'idée a été proposée la première fois par John Holland au début des années 1970[23].

Heuristiques gloutonnes

Cette section ne cite pas suffisamment ses sources (novembre 2016).

Pour l'améliorer, ajoutez des références vérifiables [comment faire ?] ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Pour le problème du voyageur de commerce, une heuristique gloutonne construit une seule solution, par une suite de décisions définitives sans retour arrière, parmi ces méthodes on cite le plus proche voisin, la plus proche insertion, la plus lointaine insertion et la meilleure insertion.

Dans la méthode du plus proche voisin, on part d'un sommet quelconque et à chacune des $(n-1)$ itérations on relie le dernier sommet atteint au sommet le plus proche au sens coût, puis on relie finalement le dernier sommet au premier sommet choisi.

Dans les méthodes d'insertion, on part d'un cycle réduit à une boucle au départ, à chaque itération on choisit un sommet libre $j$ puis on cherche la position d'insertion $i$ et $j$ de cycle qui minimise l'augmentation totale des coûts :

dans la plus lointaine insertion $j$ est le sommet libre le plus loin du cycle au sens des coûts ;
dans la plus proche insertion $j$ est le plus proche du cycle ;
enfin dans la meilleure insertion on teste tous les sommets $j$ non encore insérés et on choisit celui qui donne la plus faible augmentation du coût.

Histoire et importance

Origines et cas particuliers

Le principe d'un tel voyage est décrit dès 1832, dans un écrit d'un commis-voyageur et des itinéraires efficaces étaient référencés dans des guides[24]. Plusieurs problèmes anciens peuvent être vus comme des cas particuliers du problème ; par exemple, en 1856, William Rowan Hamilton s'était intéressé à un problème géométrique de ce type sur un dodécaèdre, d'ailleurs le terme cycle hamiltonien désigne un cycle passant par tous les sommets dans un graphe[24].

Terminologie

Le terme problème du voyageur de commerce, vient de la traduction de l'anglais américain Traveling salesman problem, qui est apparu dans les années 1930 ou 40, sans doute à l'université de Princeton où plusieurs chercheurs s'y intéressaient[24]. C'est aussi à cette période que le problème est formulé indépendamment dans plusieurs communautés de chercheurs, notamment autour de Karl Menger[24].

Développements

Le problème a alors intéressé une plus large communauté et a notamment été à l'origine de la découverte de plusieurs techniques, comme l'optimisation linéaire mixte (mixed integer programming), et la méthode de séparation et évaluation (branch-and-bound)[24].

En 1972, Richard Karp montra que le problème de décision associé est NP-complet[25].

Importance dans l'enseignement et la recherche

Le voyageur de commerce est aujourd'hui l'un des problèmes algorithmiques ayant le plus été étudiés[24]. De plus, du fait de la simplicité de son énoncé, il est souvent utilisé pour introduire l'algorithmique, d'où une relative célébrité[24].

Variantes

La variante PTSP (pour physical traveler salesman problem) consiste à visiter une et une seule fois un nombre fini dans un environnement 2D avec des obstacles[26]. La variante mTSP (pour multiple traveler salesman problem) généralise le problème à plusieurs voyageurs, lui-même se généralisant en le problème de tournées de véhicules[27].

Applications

Le problème du voyageur du commerce a de nombreuses applications[24], et a d'ailleurs été motivé par des problèmes concrets, par exemple le parcours des bus scolaires[28].

Un premier type d'application classique est bien sûr dans la logistique, par exemple pour la poste, la distribution de repas à domicile, l'inspection d'installations, etc.[28]. On peut aussi optimiser les mouvements de machines, par exemple, pour minimiser le temps total que met une fraiseuse à commande numérique pour percer n points dans une plaque de tôle[29], ou minimiser les mouvements des grands télescopes (qui sont très lents)[28].

On peut citer des applications plus surprenantes, par exemple : en biologie, le problème aide au séquençage du génome (pour relier des petits fragments en des chaînes plus grandes), et en production il est utilisé pour le test des circuits imprimés[28].

Notes et références

Notes

En général par le biais de la méthode du branch and cut.

Références

« TERMIUM Plus, « travelling salesman problem » », sur btb.termiumplus.gc.ca (consulté le 14 août 2016).
On donne ici une intuition géométrique. Mais le problème de voyageur de commerce prend en entrée une matrice de distances qui ne vérifient pas forcément l'inégalité triangulaire. Le cas métrique (où l'inégalité triangulaire est vérifiée) et le cas euclidien sont discutés plus tard dans l'article.
Patrick Siarry, Métaheuristiques : Recuits simulé, recherche avec tabous, recherche à voisinages variables, méthodes GRASP, algorithmes évolutionnaires, fourmis artificielles, essaims particulaires et autres méthodes d'optimisation, Eyrolles, 26 mars 2014, 534 p. (ISBN 978-2-212-26621-4, lire en ligne), p. 182.
On peut estimer l'ordre de grandeur du nombre d'atomes dans l'univers à 10⁸⁰.
Présent notamment dans la liste des 21 problèmes NP-complets de Karp : (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103.
(en) « The Euclidean travelling salesman problem is NP-complete », Theoretical Computer Science, vol. 4, n^o 3,‎ 1^er juin 1977, p. 237–244 (ISSN 0304-3975, DOI 10.1016/0304-3975(77)90012-3, lire en ligne, consulté le 13 septembre 2018)
(en) M. Held et R.M. Karp, « A Dynamic Programming Approach to Sequencing Problems », Journal of the Society for Industrial and Applied Mathematics, 1962, 10 (1), 196–210.
(en) Voir par exemple le site de l'université Georgia Tech.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, 2010 [détail de l’édition], chap. 15 ("Programmation dynamique"), p. 375.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, 2010 [détail de l’édition], chap. 35 : Algorithmes d'approximation.
Nicos Christofides, « Worst-case analysis of a new heuristic for the travelling salesman problem », Technical Report 388, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh,‎ 1976.
Christos H. Papadimitriou et Mihalis Yannakakis, « The traveling salesman problem with distances one and two », Mathematics of Operations Research, INFORMS, vol. 18, n^o 1,‎ 1993, p. 1--11.
(en) « New inapproximability bounds for TSP », Journal of Computer and System Sciences, vol. 81, n^o 8,‎ 1^er décembre 2015, p. 1665–1677 (ISSN 0022-0000, DOI 10.1016/j.jcss.2015.06.003, lire en ligne, consulté le 11 octobre 2020).
Anna R. Karlin, Nathan Klein et Shayan Oveis Gharan, « A (Slightly) Improved Approximation Algorithm for Metric TSP », arXiv:2007.01409 [cs, math],‎ 30 août 2020 (lire en ligne).
(en) Erica Klarreich, « Computer Scientists Break Traveling Salesperson Record », sur Quanta Magazine (consulté le 11 octobre 2020).
Sanjeev Arora, « Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems », Journal of the ACM, vol. 45, n^o 5,‎ 1998, p. 753–782 (DOI 10.1145/290179.290180).
Joseph S. B. Mitchell, « Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems », SIAM Journal on Computing, vol. 28, n^o 4,‎ 1999, p. 1 298–1 309 (ISSN 1095-7111, DOI 10.1137/S0097539796309764).
« The Gödel Prize 2010, Laudatio for S. Arora and J.S.B. Mitchell », sur EATCS.
Robert D. Carr et Santosh Vempala, « On the Held-Karp relaxation for the asymmetric and symmetric traveling salesman problems », Math. Program., vol. 100, n^o 3,‎ 2004, p. 569-587.
Rene Beier, « The Traveling Salesman Problem, the Subtour LP, and the Held-Karp Lower Bound », sur MPII.
(en) S. Lin et B. W. Kernighan (1973), « An Effective Heuristic Algorithm for the Traveling-Salesman Problem », Operations Res. 21, 498-516.
(en) G. Schrimpf, J. Schneider, H. Stamm-Wilbrandt and G. Dueck, « Record Breaking Optimization Results Using the Ruin and Recreate Principle », Journal of Computational Physics 159, 2000, 139–171.
(en) J. H. Holland, Adaptation In Natural And Artificial Systems, University of Michigan Press (1975).
David L. Applegate, Robert E. Bixby, Václav Chvátal et William J. Cook, chap. 1 « The Problem », dans The traveling Salesman Problem: A Computational Study, Princeton University Press, 2006.
(en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103.
(en-US) « Solving the Physical Traveling Salesman Problem: Tree Search and Macro Actions - IEEE Journals & Magazine », sur ieeexplore.ieee.org (consulté le 16 juillet 2018)
(en) « The multiple traveling salesman problem: an overview of formulations and solution procedures », Omega, vol. 34, n^o 3,‎ 1^er juin 2006, p. 209–219 (ISSN 0305-0483, DOI 10.1016/j.omega.2004.10.004, lire en ligne, consulté le 13 septembre 2018)
David L. Applegate, Robert E. Bixby, Václav Chvátal et William J. Cook, chap. 2 « Applications », dans The traveling Salesman Problem: A Computational Study, Princeton University Press, 2006.
(en) William Timothy Gowers (dir.), chap. VII.5 « The Influence of Mathematics:The Mathematics of Algorithm Design », dans The Princeton companion to Mathematics, Princeton et Oxford, Princeton University Press, 2008 (ISBN 978-0-691-11880-2), p. 871-878.

Voir aussi

Articles connexes

Liens externes

Applet Java, illustrant le problème du voyageur de commerce
tsplib, une bibliothèque fournissant des instances du problème
concorde, un logiciel capable de résoudre des instances du problème
Une applet utilisant l'api de google maps résolvant des instances du problème
Solveur TSP avec BING Maps résout TSP et TSPTW.
recuit simulé pour le voyageur de commerce, application en ligne
Approximation Taxonomy of Metric TSP a l'Université de Bonn
TSP dans la logistique urbaine(en) « A contribution to solving the travelling salesman problem using ant colony optimization and web mapping platforms : Application to logistics in a urban context », Codit14, IEEE,‎ septembre 2014, p. 7 (ISBN 978-1-4799-6773-5, lire en ligne)

Portail de l'informatique théorique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[8] En général par le biais de la méthode du branch and cut.

[1] « TERMIUM Plus, « travelling salesman problem » », sur btb.termiumplus.gc.ca (consulté le 14 août 2016).

[2] On donne ici une intuition géométrique. Mais le problème de voyageur de commerce prend en entrée une matrice de distances qui ne vérifient pas forcément l'inégalité triangulaire. Le cas métrique (où l'inégalité triangulaire est vérifiée) et le cas euclidien sont discutés plus tard dans l'article.

[3] Patrick Siarry, Métaheuristiques : Recuits simulé, recherche avec tabous, recherche à voisinages variables, méthodes GRASP, algorithmes évolutionnaires, fourmis artificielles, essaims particulaires et autres méthodes d'optimisation, Eyrolles, 26 mars 2014, 534 p. (ISBN 978-2-212-26621-4, lire en ligne), p. 182.

[4] On peut estimer l'ordre de grandeur du nombre d'atomes dans l'univers à 10⁸⁰.

[5] Présent notamment dans la liste des 21 problèmes NP-complets de Karp : (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103.

[6] (en) « The Euclidean travelling salesman problem is NP-complete », Theoretical Computer Science, vol. 4, n^o 3,‎ 1^er juin 1977, p. 237–244 (ISSN 0304-3975, DOI 10.1016/0304-3975(77)90012-3, lire en ligne, consulté le 13 septembre 2018)

[7] (en) M. Held et R.M. Karp, « A Dynamic Programming Approach to Sequencing Problems », Journal of the Society for Industrial and Applied Mathematics, 1962, 10 (1), 196–210.

[9] (en) Voir par exemple le site de l'université Georgia Tech.

[10] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, 2010 [détail de l’édition], chap. 15 ("Programmation dynamique"), p. 375.

[Cormen-11] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein (trad. de l'anglais), Algorithmique : Cours avec 957 exercices et 158 problèmes, Dunod, 2010 [détail de l’édition], chap. 35 : Algorithmes d'approximation.

[12] Nicos Christofides, « Worst-case analysis of a new heuristic for the travelling salesman problem », Technical Report 388, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh,‎ 1976.

[13] Christos H. Papadimitriou et Mihalis Yannakakis, « The traveling salesman problem with distances one and two », Mathematics of Operations Research, INFORMS, vol. 18, n^o 1,‎ 1993, p. 1--11.

[14] (en) « New inapproximability bounds for TSP », Journal of Computer and System Sciences, vol. 81, n^o 8,‎ 1^er décembre 2015, p. 1665–1677 (ISSN 0022-0000, DOI 10.1016/j.jcss.2015.06.003, lire en ligne, consulté le 11 octobre 2020).

[15] Anna R. Karlin, Nathan Klein et Shayan Oveis Gharan, « A (Slightly) Improved Approximation Algorithm for Metric TSP », arXiv:2007.01409 [cs, math],‎ 30 août 2020 (lire en ligne).

[16] (en) Erica Klarreich, « Computer Scientists Break Traveling Salesperson Record », sur Quanta Magazine (consulté le 11 octobre 2020).

[17] Sanjeev Arora, « Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems », Journal of the ACM, vol. 45, n^o 5,‎ 1998, p. 753–782 (DOI 10.1145/290179.290180).

[18] Joseph S. B. Mitchell, « Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems », SIAM Journal on Computing, vol. 28, n^o 4,‎ 1999, p. 1 298–1 309 (ISSN 1095-7111, DOI 10.1137/S0097539796309764).

[19] « The Gödel Prize 2010, Laudatio for S. Arora and J.S.B. Mitchell », sur EATCS.

[CarrV04-20] Robert D. Carr et Santosh Vempala, « On the Held-Karp relaxation for the asymmetric and symmetric traveling salesman problems », Math. Program., vol. 100, n^o 3,‎ 2004, p. 569-587.

[21] Rene Beier, « The Traveling Salesman Problem, the Subtour LP, and the Held-Karp Lower Bound », sur MPII.

[22] (en) S. Lin et B. W. Kernighan (1973), « An Effective Heuristic Algorithm for the Traveling-Salesman Problem », Operations Res. 21, 498-516.

[23] (en) G. Schrimpf, J. Schneider, H. Stamm-Wilbrandt and G. Dueck, « Record Breaking Optimization Results Using the Ruin and Recreate Principle », Journal of Computational Physics 159, 2000, 139–171.

[24] (en) J. H. Holland, Adaptation In Natural And Artificial Systems, University of Michigan Press (1975).

[ApplegateBCC-25] David L. Applegate, Robert E. Bixby, Václav Chvátal et William J. Cook, chap. 1 « The Problem », dans The traveling Salesman Problem: A Computational Study, Princeton University Press, 2006.

[26] (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, 1972 (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103.

[27] (en-US) « Solving the Physical Traveling Salesman Problem: Tree Search and Macro Actions - IEEE Journals & Magazine », sur ieeexplore.ieee.org (consulté le 16 juillet 2018)

[28] (en) « The multiple traveling salesman problem: an overview of formulations and solution procedures », Omega, vol. 34, n^o 3,‎ 1^er juin 2006, p. 209–219 (ISSN 0305-0483, DOI 10.1016/j.omega.2004.10.004, lire en ligne, consulté le 13 septembre 2018)

[ApplegateBCC_appli-29] David L. Applegate, Robert E. Bixby, Václav Chvátal et William J. Cook, chap. 2 « Applications », dans The traveling Salesman Problem: A Computational Study, Princeton University Press, 2006.

[30] (en) William Timothy Gowers (dir.), chap. VII.5 « The Influence of Mathematics:The Mathematics of Algorithm Design », dans The Princeton companion to Mathematics, Princeton et Oxford, Princeton University Press, 2008 (ISBN 978-0-691-11880-2), p. 871-878.