Inégalité triangulaire
En géométrie, l'inégalité triangulaire est le fait que, dans un triangle, la longueur d'un côté est inférieure à la somme des longueurs des deux autres côtés. Cette inégalité est relativement intuitive. Dans la vie ordinaire, comme dans la géométrie euclidienne, cela se traduit par le fait que la ligne droite est le plus court chemin : le plus court chemin d'un point A à un point B est d'y aller tout droit, sans passer par un troisième point C qui ne serait pas sur la ligne droite.
De façon plus abstraite, cette inégalité correspond au fait que la distance directe est une valeur minimale de distance. Elle est aussi une propriété ou condition nécessaire à la définition d'une bonne distance. Cette distance est un choix possible en métrique mathématique, mais pas forcément le meilleur, suivant les cas et les usages.
Énoncés
En géométrie
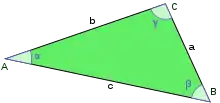
Dans un plan euclidien, soit un triangle ABC. Alors les longueurs AB, AC et CB vérifient les trois inégalités suivantes :
- ;
- ;
- .
Réciproquement, étant données trois longueurs dont chacune (ou, ce qui suffit : la plus grande) est inférieure à la somme des deux autres, il existe un triangle ayant ces longueurs de côté.
Une propriété se déduit de ces inégalités : Cette dernière inégalité entraîne que dans un triangle, la longueur d'un côté est supérieure à la différence des longueurs des deux autres. Ce qui apparaît donc comme une propriété relative à la topologie du triangle.
Une autre les complète : .
Pour les nombres complexes
En utilisant une représentation complexe du plan euclidien, on peut noter
On obtient cette formulation équivalente.
Pour , on a :
- ;
- .
Généralisation aux espaces préhilbertiens
Soit un espace préhilbertien réel. On note la norme associée au produit scalaire. Pour , on vérifie alors :
- ;
- .
(Tout espace préhilbertien complexe est un espace préhilbertien réel, pour le produit scalaire , qui induit la même norme que le produit hermitien .)
Point de vue axiomatique
Soient E un ensemble et . On dit que d est une distance sur E si :
La troisième propriété demandée à pour être une distance est de vérifier l'inégalité triangulaire. Jointe à la première, elle entraîne :
et plus généralement, pour toute partie non vide A de E, (voir « Distance d'un point à une partie »).
Réciproquement, .
Tout espace vectoriel normé — en particulier — est naturellement muni d'une distance , définie par , pour laquelle la majoration se réécrit :
- .
Démonstration
Soient un espace préhilbertien réel et .
Inégalité
On a .
Par l'inégalité de Cauchy-Schwarz, .
D'où .
Et donc .
(Si est le plan euclidien, identifié au plan complexe muni du produit scalaire ⟨u, v⟩ = Re(u v) — dont la norme associée est le module — l'inégalité de Cauchy-Schwarz utilisée ici est, de même que le cas d'égalité ci-dessous, une propriété élémentaire des nombres complexes.)
Cas d'égalité
Supposons que et .
Par ce qui précède, on a donc .
Donc, par le cas d'égalité de Cauchy-Schwarz, avec .
Finalement, on a bien , avec .