Objet impossible
Un objet impossible est la représentation d'une construction fictive d'un objet contraire aux lois physiques connues de la nature.

Il illustre un problème de topologie mathématique entre la dimension de la représentation (dessin dans le plan ou espace en deux dimensions) et celle de l'objet fictif (dans l'espace en trois dimensions).
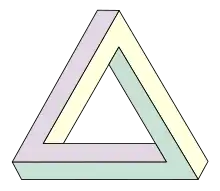
Comme l'illustre le triangle de Penrose ci-contre, le dessin plan introduit une ambiguïté car on ne peut — ou on ne sait pas l'interpréter comme l'exacte représentation, en projection sur un plan, d'un objet réel. Donc, l'objet tridimensionnel théorique qui devrait correspondre au dessin est impossible.
Du fait de ce paradoxe entre logique et réalité, qui s'étend à d'autres sphères (impossibilité culturelle), les objets impossibles ouvrent ainsi à de nombreuses curiosités mathématiques et inspirations artistiques.
Description et dessins ou objets apparentés

On peut distinguer les objets impossibles des « figures indécidables » par le fait que ces dernières représentent des objets qui peuvent réellement exister, bien que sous plusieurs formes selon l'interprétation qui en est décidée : exemple du cube de Necker qui, par opération mentale, change d'orientation ; ou celui des cubes qui s'emboitent petit devant en saillie ou grand derrière écorné par le petit[pas clair][1]. Lorsque les arêtes sont épaissies / orientées / ombrées, ces cubes deviennent irréalisables, tel le cube impossible.
L'objet impossible, par son dessin, peut user « d'illusions d'optiques et de logique », mais si ces dernières sont mises en œuvre aussi pour illustrer un paradoxe, ce paradoxe n'est en général qu'apparent ou indécidable, sans mener à l'impossibilité mentale. L'illusion peut à l'inverse ne pas être attribuée à un objet impossible, « selon le contexte ou le regard qu'on y porte » : par exemple une bouteille sans fond remplie d'eau sera trouvée impossible sur une photo, vidéo ou montage tenus pour réalistes, ou bien fort possible et réelle considérant qu'il s'agit d'un instantané après avoir enlevé le fond très rapidement, ou que l'eau est congelée.
Également à cet égard, on peut rapprocher les objets impossibles des « objets introuvables » du Catalogue de Jacques Carelman ou du musée de Serge Brussolo, qui sont contraires, non pas aux lois de la physique, mais à celles de la raison ou des valeurs morales, c'est-à-dire basés non pas sur une illusion de représentation mais sur un paradoxe : en l'occurrence une contradiction entre la fonction de l'objet et sa construction (par exemple, un préservatif en dentelle, un char d'assaut en porcelaine, etc.). Ceci paraitra possible et réel mais inutile ou artistique, voire impossible à certains.
Enfin, ou peut parler de « figure impossible » (ou dessin inexact) au sujet d'une représentation nécessairement « trichée » à certains niveaux afin de paraitre assez satisfaisante (complète, interprétable), pour un objet possible (réel ou non) qui ne se serait représenté en dimension inférieure (le plan) que de façon trop ambiguë (indécidable) ou pas assez signifiante voire triviale : par exemple, un simple point, un trait ou une sinusoïde nous suggèrent ces formes simples plutôt qu'une spirale qu'on ne saura représenter autrement à plat, sauf à ajouter des conventions de superposition de trait, et/ou une épaisseur ombrée. Autre exemple plus concret, les Égyptiens dessinaient le corps humain avec la tête de profil mais l’œil de face, les épaules et bras de face jusqu'aux doigts visibles, le torse de côté, le bassin de face, et les jambes de profil[2]. Ce n'est bien sûr pas l'objet « homme » qui était impossible à leur yeux, ni la représentation qui devait se plier à des règles (représenter tous les éléments canoniques, quitte à synthétiser deux projections), alors qu'avec notre culture moderne privilégiant une exactitude réaliste à une exactitude représentative, c'est le dessin ou l'objet représenté qui devient impossible.
Exemples notables
- Le cube impossible.
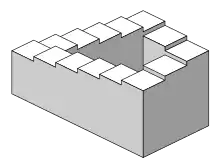
- L'escalier de Penrose.
- Le triangle de Penrose.
- L'Unobtainium.
- Le blivet.
- Les anneaux borroméens (mais ce dernier exemple est réalisable avec des cercles à peine déformés).
L'artiste suédois Oscar Reutersvärd est le père des figures impossibles. Il fut le premier à créer de telles figures.
Un bon exemple de monde défini par des objets impossibles est l'œuvre de l'artiste néerlandais Maurits Cornelis Escher, dont (par exemple) les escaliers symétriques mènent inexorablement à une boucle infinie. Un tel escalier sans fin, dit aussi de Penrose, est constructible, mais en biaisant sa représentation graphique (perspective) et la logique (marches supposées horizontales)[réf. nécessaire].
Notes et références
- Motif cubique(petit cube imbriqué dans un grand cube, ou l'inverse)
- Exemple de représentation d'une personne, et ses conventions artistiques
Annexes
Articles connexes
- Illusion d'optique
- Anamorphose
- Coïncidence mathématique
- Roger Penrose, à qui l'on doit certains de ces objets impossibles.
- Maurits Cornelis Escher
Liens externes
- Le triangle impossible en vidéo, sur le site www.triangleimpossible.com
- (en) Real Escher Objects, sur le site www.cs.technion.ac.il
- Portail des mathématiques