Nombre de croisements (théorie des graphes)

Pendant la Seconde Guerre mondiale, le mathématicien hongrois Pál Turán a été contraint de travailler dans une usine de briques, poussant des wagons de briques des fours aux sites de stockage. L'usine avait des pistes de chaque four à chaque site de stockage, et les wagons étaient plus difficiles à pousser aux points où les pistes se croisaient, d'où Turán a été conduit à poser son problème d'usine de brique: comment les fours, les sites de stockage et les pistes être organisé pour minimiser le nombre total de croisements ? Mathématiquement, les fours et les sites de stockage peuvent être formalisés comme les sommets d'un graphe biparti complet, avec les pistes comme arêtes. Un plan d'usine peut être représenté comme un dessin de ce graphe, le problème devient donc : quel est le nombre de croisements d'un graphe biparti complet[7] ?

Kazimierz Zarankiewicz a tenté de résoudre le problème de l'usine de briques de Turán[8] ; sa preuve contenait une erreur, mais il a établi un majorant correct :

${\displaystyle {\textrm {cr}}(K_{m,n})\leq \left\lfloor {\frac {n}{2}}\right\rfloor \left\lfloor {\frac {n-1}{2}}\right\rfloor \left\lfloor {\frac {m}{2}}\right\rfloor \left\lfloor {\frac {m-1}{2}}\right\rfloor }$

pour le nombre de croisements du graphe biparti complet K_m,n. Cette borne est conjecturée être le nombre de croisements pour tous les graphes bipartis complets[9].

Le problème de la détermination du nombre de croisements d'un graphe complet a été posé pour la première fois par Anthony Hill en 1960[10]. Hill et son collaborateur John Ernest étaient deux artistes constructivistes fascinés par les mathématiques. Ils ont non seulement formulé ce problème, mais ont également proposé une conjecture pour ce nombre de croisements, que Richard K. Guy a publiée en 1960[10]. On sait qu'il existe toujours un tracé avec

${\displaystyle {\textrm {cr}}(K_{p})\leq {\frac {1}{4}}\left\lfloor {\frac {p}{2}}\right\rfloor \left\lfloor {\frac {p-1}{2}}\right\rfloor \left\lfloor {\frac {p-2}{2}}\right\rfloor \left\lfloor {\frac {p-3}{2}}\right\rfloor }$

croisements. Cette formule donne les valeurs 1, 3, 9, 18, 36, 60, 100, 150 pour p = 5, ..., 12 ; (suite A000241 de l'OEIS). La conjecture est qu'il ne peut y avoir de meilleur tracé, de sorte que cette formule donne le nombre optimal de croisements pour les graphes complets. Une formulation indépendante de la même conjecture a été faite par Thomas L. Saaty en 1964[11].

Saaty a en outre vérifié que cette formule donne le nombre optimal de croisements pour p ≤ 10 et Pan et Richter ont montré qu'elle était également optimale pour p = 11, 12[12].

La conjecture d'Albertson, formulée par Michael O. Albertson en 2007, déclare que, parmi tous les graphes de nombre chromatique n, le graphe complet K_n a le nombre minimum de croisements. On sait aujourd'hui que la conjecture d'Albertson est valable pour n ≤ 16.[13]

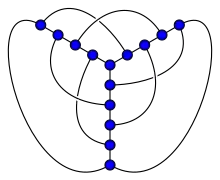
Les plus petits graphes cubiques avec les nombres de croisement 1..., 8 et 11 sont connus (suite A110507 de l'OEIS). Le plus petit graphe cubique à 1 croisement est le graphe biparti complet K_3,3, avec 6 sommets. Le plus petit graphe cubique à 2 croisements est le graphe de Petersen, avec 10 sommets. Le plus petit graphe cubique à 3 croisements est le graphe de Heawood, avec 14 sommets. Le plus petit graphe cubique à 4 croisements est le graphe de Möbius-Kantor, avec 16 sommets. Le plus petit graphe cubique à 5 croisements est le graphe de Pappus, avec 18 sommets. Le plus petit graphe cubique à 6 croisements est le graphe de Desargues, avec 20 sommets. Aucun des quatre graphes cubiques à 7 croisements, avec 22 sommets, n'est parfaitement connu[14]. Les plus petits graphes cubiques à 8 croisements incluent le graphe de Nauru et le graphe de McGee ou (3,7)-cage, avec 24 sommets[15]. Les plus petits graphes cubiques à 11 croisements incluent le graphe de Coxeter avec 28 sommets.

En 2009, Pegg et Exoo ont conjecturé que le plus petit graphe cubique avec un nombre de croisements valant 13 est le graphe de Tutte–Coxeter, valant 170 est le 12-cage de Tutte[15]^,[16].