Graphe de Petersen
Le graphe de Petersen est, en théorie des graphes, un graphe particulier possédant 10 sommets et 15 arêtes.
| Graphe de Petersen | |
 Schéma classique du graphe de Petersen, sous la forme d'un pentagone et d'un pentagramme concentriques, reliés par cinq rayons. | |
| Nombre de sommets | 10 |
|---|---|
| Nombre d'arêtes | 15 |
| Distribution des degrés | 3-régulier |
| Rayon | 2 |
| Diamètre | 2 |
| Maille | 5 |
| Automorphismes | 120 (S5) |
| Nombre chromatique | 3 |
| Indice chromatique | 4 |
| Propriétés | Cage Cubique Distance-transitif Distance-unité Fortement régulier Hypohamiltonien Graphe de Moore Snark Symétrique |
Il s'agit d'un petit graphe qui sert d'exemple et de contre-exemple pour plusieurs problèmes de la théorie des graphes. Il porte le nom du mathématicien Julius Petersen, qui l'introduisit en 1898 en tant que plus petit graphe cubique sans isthme dont les arêtes ne peuvent être colorées avec trois couleurs[1]. Il a cependant été mentionné par Alfred Kempe pour la première fois 12 ans auparavant, en 1886[2].
Donald Knuth explique dans The Art of Computer Programming que le graphe de Petersen est « une configuration remarquable qui sert de contre-exemple à de nombreuses prédictions optimistes sur ce qui devrait être vrai pour tous les graphes[3] ».
Constructions
Le graphe de Petersen est le complémentaire du line graph du graphe complet . C'est également le graphe de Kneser ; il est donc possible de construire le graphe de Petersen en considérant un sommet pour chaque couple d'un ensemble de 5 éléments, et en reliant deux sommets si les couples correspondants sont disjoints.
Géométriquement, le graphe de Petersen est le graphe formé par les sommets et les arêtes de l'hémi-dodécaèdre (en), un dodécaèdre dont les sommets, arêtes et faces opposés sont identifiés deux à deux.
Propriétés
Propriétés générales
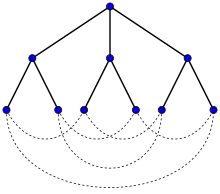
Le graphe de Petersen est une (3,5)-cage, c'est-à-dire un graphe minimal en nombre de sommets ayant une maille de 5 et étant cubique. Il s'agit de l'unique (3,5)-cage et sa taille coïncide avec la borne de Moore, une borne inférieure sur le nombre de sommets que peut avoir une cage. Un tel graphe est qualifié de graphe de Moore.
Le diamètre du graphe de Petersen, l'excentricité maximale de ses sommets, ainsi que son rayon, l'excentricité minimale de ses sommets, sont égaux à 2. Cela entraîne que tous ses sommets appartiennent à son centre. C'est aussi le plus grand graphe cubique de diamètre 2.
Le graphe de Petersen est 3-sommet-connexe et 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté, il faut le priver au minimum de 3 sommets ou de 3 arêtes. Comme il est régulier de degré 3, ce nombre est optimal. Le graphe de Petersen est donc un graphe optimalement connecté.
Le graphe de Petersen possède 2 000 arbres couvrants, le maximum parmi les graphes cubiques à 10 sommets[4],[5].
Plongements
Le graphe de Petersen n'est pas planaire. Tout graphe non-planaire possède comme mineur soit le graphe complet , soit le graphe biparti complet ; le graphe de Petersen possède les deux.
Le dessin plan le plus courant schématise le graphe de Petersen sous la forme d'un pentagramme inclus dans un pentagone, et possède cinq croisements. Ce dessin ne minimise pas le nombre de croisements ; il est possible de représenter le graphe de Petersen avec seulement deux croisements. Sur un tore, le graphe de Petersen peut être représenté sans croisement ; c'est donc un graphe torique et son genre est égal à 1.
Le graphe de Petersen est le plus petit graphe cubique dont l'invariant de Colin de Verdière est μ = 5.
La plus simple surface non orientable sur laquelle le graphe de Petersen peut être plongé sans croisement est le plan projectif. Ce plongement est donné par la construction à partir de l'hémi-dodécaèdre.
Le graphe de Petersen est également un graphe distance-unité : il peut s'obtenir à partir d'une collection de points du plan euclidien en reliant par une arête toutes les paires de points étant à une distance de 1. Dans une telle représentation, plusieurs arêtes se croisent.
Propriétés algébriques
Le graphe de Petersen est fortement régulier. Il est également symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Il est donc également arête-transitif et sommet-transitif. Le graphe de Petersen est l'unique graphe cubique symétrique à 10 sommets et sa notation dans le Foster Census, le catalogue classifiant tous les graphes cubiques symétriques, est F10A[6],[7].
Le groupe d'automorphismes du graphe de Petersen est le groupe symétrique ; un groupe d'ordre 120. L'action de sur le graphe de Petersen découle de sa construction comme graphe de Kneser. Tout homomorphisme du graphe de Petersen sur lui-même qui n'identifie pas des sommets adjacents est un automorphisme. Les représentations planaires du graphe de Petersen ne peuvent pas représenter la totalité de son groupe symétrique.
Malgré son degré de symétrie élevé, le graphe de Petersen n'est pas un graphe de Cayley, le plus petit graphe sommet-transitif à ne pas l'être.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Petersen est : . Ce polynôme caractéristique n'admet que des racines entières. Le graphe de Petersen est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.
Chemins et cycles hamiltoniens

Le graphe de Petersen possède 240 chemins hamiltoniens distincts mais n'est pas hamiltonien, donc n'a pas de cycle hamiltonien. C'est le plus petit graphe cubique sans isthme à ne pas être hamiltonien. Il est également hypohamiltonien, c'est-à-dire que la suppression de n'importe quel sommet du graphe de Petersen suffit à le rendre hamiltonien. Il s'agit du plus petit graphe hypohamiltonien[8],[9].
En tant que graphe connexe fini sommet-transitif et non-hamiltonien, il offre une contre-exemple à une variante de la conjecture de Lovász (en) qui affirme que tous les graphes sommet-transitifs sont hamiltoniens. Mais la formulation canonique de la conjecture ne demande qu'un chemin hamiltonien et est donc vérifiée par le graphe de Petersen.
Seuls cinq graphes finis sommet-transitifs et non-hamiltoniens sont connus : le graphe complet K2, le graphe de Petersen, le graphe de Coxeter et les deux graphes obtenus à partir du graphe de Petersen et du graphe Coxeter en remplaçant chaque sommet par un triangle[7].
Si un graphe est 2-connexe, r-régulier avec au plus 3r + 1 sommets, alors G est hamiltonien ou G est le graphe de Petersen[1].
Prouver que le graphe de Petersen n'admet pas de cycle hamiltonien C peut se faire en décrivant les graphes 3-réguliers hamiltoniens et en prouvant qu'aucun d'eux n'est le graphe de Petersen car ils seront tous de maille inférieure à 5. Tout graphe cubique hamiltonien à dix sommets est constitué d'un cycle C et de cinq cordes. Si une corde relie deux sommets qui sont à une distance deux ou trois dans le cycle C, alors le graphe considéré admet un 3-cycle ou un 4-cycle. Si deux cordes relient deux sommets opposés dans C à des sommets qui sont tous deux à une distance de 4, alors il y a de nouveau un 4-cycle. Le seul cas restant est l'échelle de Möbius, le graphe formé en reliant chaque sommet de C au sommet qui lui est opposé (c'est-à-dire à une distance de 5). Mais l'échelle de Möbius admet aussi un 4-cycle. Le graphe de Petersen est de maille 5, c'est-à-dire que la longueur de son plus court cycle est 5. En conséquence, il n'est pas hamiltonien.
Coloration
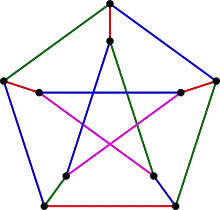

Le nombre chromatique du graphe de Petersen est 3. C'est-à-dire qu'il est possible de colorer ses sommets avec 3 couleurs, de telle façon que deux sommets reliés par une arête soient d'une couleur différente. Ce nombre est minimal. La 3-coloration de la figure ci-contre est une coloration équitable, où les trois couleurs sont à peu près également représentées.
L'indice chromatique du graphe de Petersen est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal. Le graphe de Petersen est donc un snark, un graphe connexe, sans isthme, cubique, de maille au moins 5 et d'indice chromatique 4. Il s'agit du plus petit snark possible et ce fut le seul snark connu de 1898 à 1946, jusqu'à ce que Danilo Blanuša exhibe deux autres exemples, le premier snark de Blanuša et le second snark de Blanuša[10].
Le théorème du snark, un résultat conjecturé par W. T. Tutte et prouvé en 2001 par Robertson, Sanders, Seymour et Thomas, affirme que tout snark admet le graphe de Petersen comme mineur[11].
Il est possible de compter les colorations distinctes du graphe de Petersen, en fonction du nombre de couleurs autorisé. Cela donne une fonction polynomiale et le polynôme qui lui est associé est qualifié de polynôme chromatique. Ce polynôme de degré 10 admet pour racines tous les entiers positifs ou nuls strictement inférieurs à 3. Il est égal à : .
Le graphe possède un indice chromatique fractionnel de 3, montrant que la différence entre l'index chromatique et l'index chromatique fractionnel d'un graphe peut être égale à 1. La conjecture de Goldberg-Seymour suppose qu'il s'agit de la plus grande différence possible.
Le nombre de Thue (une variante de l'indice chromatique) du graphe de Petersen est égal à 5.
Notes et références
- (en) D. A. Holton et J. Sheehan, The Petersen Graph, Cambridge, CUP, (ISBN 978-0-521-43594-9, LCCN 93210238, DOI 10.2277/0521435943, lire en ligne), « 32 »(Archive • Wikiwix • Archive.is • Google • Que faire ?) (consulté le )
- (en) A. B. Kempe, « A memoir on the theory of mathematical form », Philos. Trans. R. Soc., vol. 177, , p. 1–70
- (en) Donald E. Knuth, The Art of Computer Programming, vol. 4 : pre-fascicle 0A. A draft of section 7: Introduction to combinatorial searching, Addison-Wesley
- (en) Dmitry Jakobson et Igor Rivin, On some extremal problems in graph theory, , arXiv:math.CO/9907050
- (en) L. Valdes, « Extremal properties of spanning trees in cubic graphs », Congressus Numerantium, vol. 85, , p. 143–160
- (en) M. Conder et P. Dobcsányi, « Trivalent Symmetric Graphs Up to 768 Vertices », J. Combin. Math. Combin. Comput., vol. 40, , p. 41-63
- (en) G. Royle, Cubic Symmetric Graphs (The Foster Census), 2001
- R. Sousselier, Problèmes plaisants et délectables, vol. 7, , p. 405–406
- T. Gaudin, P. Herz et Rossi, Solution du problème No. 29, vol. 8, , p. 214–218
- (en) Danilo Blanuša, « Problem četiriju boja », Glasnik Mat. Fiz. Astr. Ser II, vol. 1, , p. 31–42
- (en) Ed, Jr. Pegg, Book Review : The Colossal Book of Mathematics, vol. 49, (lire en ligne), chap. 9, p. 1084–1086.
Voir aussi
Articles connexes
Liens externes
- (en) Eric W. Weisstein, « Petersen Graph », sur MathWorld
- (en) Andries E. Brouwer, « The Petersen graph », site personnel de l'auteur
- (en) Petersen colouring conjecture
- Portail des mathématiques