Rayon (théorie des graphes)
En théorie des graphes, le rayon d'un graphe est l'excentricité minimale de ses sommets, c'est-à-dire la plus petite distance à laquelle puisse se trouver un sommet de tous les autres. Le centre d'un graphe est formé de l'ensemble de ses sommets d'excentricité minimale.
Pour les articles homonymes, voir Rayon.
L'excentricité maximale est appelée diamètre.
La distance entre deux sommets dans un graphe est définie par la longueur d'un plus court chemin entre ces deux sommets.
Exemples
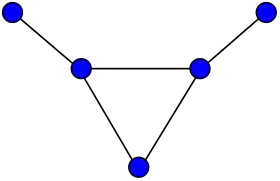Le Graphe taureau a un rayon de 2. Son centre est constitué des trois sommets formant un triangle.
Le graphe hexaédrique a un rayon de 3 et un diamètre de 3 : tous ses sommets appartiennent à son centre.
Le Snark de Szekeres a un rayon de 6.
Portail de l'informatique théorique 
Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.