Modèle de Goodwin
Le modèle de Goodwin, parfois appelé modèle de lutte des classes de Goodwin, est un modèle de fluctuations économiques endogènes proposé pour la première fois par l'économiste américain Richard Goodwin en 1967. Il combine des aspects du modèle de croissance de Harrod et Domar avec la courbe de Phillips pour générer des cycles endogènes de l'activité économique (production, chômage et salaires), contrairement à la plupart des modèles macroéconomiques modernes dans lesquels les mouvements des agrégats économiques sont induits par des chocs supposés de manière exogène. Depuis la publication de Goodwin en 1967, le modèle a été étendu et appliqué de diverses manières.
La production est donnée par la fonction de production agrégée , où :
- q est la production agrégée
- ℓ est l'utilisation du travail
- k est le capital (homogène)
- a est la productivité du travail
- σ est le ratio capital-production, une constante.
Toutes ces variables sont fonctions du temps, bien que les indices de temps aient été supprimés par commodité.
Contrairement au modèle Harrod-Domar, on suppose une utilisation complète du capital. Par conséquent, en tout temps. Le taux d'emploi est donné par , où n est la population active totale qui croît au taux β . De plus, la productivité du travail a, est supposée augmenter également au taux α. Notons que dans ce cas, le taux de croissance du taux d'emploi est donné par .
Le taux de croissance du niveau absolu de l'emploi est à son tour donné par .
On suppose que les salaires changent selon une relation de courbe de Phillips linéarisée donnée par .
En d'autres termes, si le marché du travail est « serré » (l'emploi est déjà élevé), il y a une pression à la hausse sur les salaires et vice versa dans un marché du travail «laxiste». C'est l'aspect du modèle qui peut être vaguement associé à la partie «lutte de classe» de son nom, cependant, ce type de courbe de Phillips peut être trouvé dans de nombreux modèles macroéconomiques.
La part des travailleurs dans la production est u, qui par définition est .
Par conséquent, le taux de croissance de la part des travailleurs est .
La part du travail dans la production augmente avec les salaires mais diminue avec la croissance de la productivité car il faut moins de travailleurs pour produire la même quantité de production.
Enfin, nous avons l'équation d'accumulation du capital et le taux de croissance de la production qui en résulte (puisque k et q croissent au même taux en supposant une pleine utilisation du capital et des rendements d'échelle constants). On suppose que les travailleurs consomment leurs salaires et que les propriétaires du capital épargnent une partie de leurs profits (à noter que le modèle se généralise au cas où les capitalistes épargnent plus que les travailleurs) et que le capital se déprécie au delta des taux. Le taux de croissance de la production et du capital est alors donné par .
Cela implique à son tour que .
Solution
Les deux équations différentielles
sont les équations clés du modèle et sont en fait les équations Lotka-Volterra (qui sont utilisées en biologie pour modéliser l'interaction prédateur-proie).
Bien que le modèle puisse être résolu explicitement, il est intéressant d'analyser la trajectoire de l'économie en termes de diagramme de phase. En définissant les deux équations ci-dessus égales à zéro, nous obtenons les valeurs de u et v pour lesquelles la croissance de v et la croissance u, respectivement, sont nulles.
Ces deux lignes (ainsi que les restrictions de paramètres qui garantissent que ni u ni v ne peuvent dépasser 1) divisent l'orthant positif en quatre régions. La figure ci-dessous indique avec des flèches le mouvement de l'économie dans chaque région. Par exemple, dans la région nord-ouest (emploi élevé, faible part du travail dans la production), l'économie se déplace vers le nord-est (l'emploi augmente, la part des travailleurs augmente). Une fois qu'il aura franchi la ligne u*, il commencera à se déplacer vers le sud-ouest.

La figure ci-dessous illustre l'évolution de la production potentielle (production au plein emploi), de la production réelle et des salaires au fil du temps.
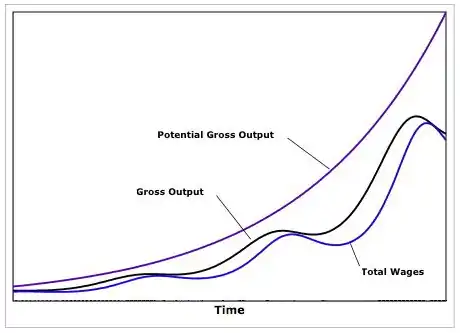
Comme on peut le voir, le modèle de Goodwin peut générer des fluctuations endogènes de l'activité économique sans s'appuyer sur des hypothèses étrangères de chocs extérieurs, que ce soit du côté de la demande ou de l'offre.
Le modèle a été appliqué et étendu par de nombreux économistes depuis sa première présentation en 1967.
Statistiques
 Part des salaires (ligne bleue) et taux d'emploi (ligne rouge) aux États-Unis. Selon le modèle de Goodwin, la part des salaires devrait être inférieure au taux d'emploi. Cela semble être le cas ne serait-ce que par un petit décalage dans le temps
Part des salaires (ligne bleue) et taux d'emploi (ligne rouge) aux États-Unis. Selon le modèle de Goodwin, la part des salaires devrait être inférieure au taux d'emploi. Cela semble être le cas ne serait-ce que par un petit décalage dans le temps
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Goodwin model (economics) » (voir la liste des auteurs).
Voir aussi
Articles connexes
Bibliographie
- (en) Richard M. Goodwin, « A Growth Cycle », dans CH Feinstein, Socialism, Capitalism and Economic Growth, Cambridge, Cambridge University Press,
- (en) Richard M. Goodwin, Chaotic Economic Dynamics, Oxford University Press,
- (en) Peter Flaschel, The Macrodynamics of Capitalism, Berlin, Springer Verlag, , 2e éd., chap. 4.3Éléments pour une synthèse de Marx, Keynes et Schumpeter
- Portail de l’économie