Graphe de Rado

En mathématiques, et plus précisément en théorie des graphes, le graphe de Rado, appelé également graphe d'Erdős–Rényi ou graphe aléatoire, est un graphe infini dénombrable étudié au début des années 1960 par Richard Rado, Paul Erdős et Alfréd Rényi, caractérisé par la propriété d’extension, qui implique qu’il contient (en tant que sous-graphe) n'importe quel graphe fini ou dénombrable.

Le graphe de Rado.

Il en existe plusieurs constructions ; c'est en particulier (presque sûrement) le graphe aléatoire obtenu en choisissant au hasard pour chaque paire de sommets s'ils sont connectés ou non.

Historique

Le graphe de Rado fut construit par Wilhelm Ackermann en 1937 à partir des ensembles héréditairement finis (en) (plus exactement, il décrivit un graphe orienté à partir duquel on obtient le graphe de Rado en supprimant l'orientation). Dans leur travail sur les graphes aléatoires, Paul Erdős et Alfréd Rényi le construisirent comme un graphe aléatoire infini et montrèrent qu'il possède un nombre infini d'automorphismes par un argument qui permettrait également d'en prouver l'unicité. Richard Rado le redécouvrit en tant que graphe universel, et en donna une construction déterministe essentiellement équivalente à celle d'Ackermann.

Constructions

Écriture binaire

Ackermann et Rado donnèrent une construction explicite utilisant le prédicat BIT (en)[1]. Identifiant les sommets du graphe et les entiers naturels 0, 1, 2,..., une arête relie les sommets x et y (avec x < y) si et seulement si le bit de rang x de la représentation binaire de y vaut 1. Par exemple, il y a un lien entre x = 2 et y = 4 = 1002, mais non entre x = 1 et y.

Graphes aléatoires

Le graphe de Rado apparaît presque sûrement quand on applique le modèle de graphe aléatoire développé par Erdős et Rény à un ensemble dénombrable de sommets. Plus précisément, choisissant indépendamment pour chaque paire de sommets avec probabilité p (0 < p < 1) si ces sommets sont reliés par une arête, le graphe résultant est presque sûrement (c'est-à-dire avec probabilité 1) isomorphe au graphe de Rado[2] ; c'est ce résultat qui justifie l'article défini dans l'expression « le graphe aléatoire » qui le désigne parfois.

Un graphe isomorphe au graphe complémentaire du graphe de Rado peut être obtenu (presque sûrement) par la même construction en choisissant les arêtes avec une probabilité 1–p, ce qui montre que le graphe de Rado est auto-complémentaire[3].

Autres constructions

La propriété d'extension caractérise le graphe de Rado, et permet de montrer que de nombreuses constructions lui sont isomorphes.

Dans les constructions d'Ackermann en 1937, les sommets du graphe de Rado sont les ensembles héréditairement finis (c'est-à-dire les ensembles finis dont les éléments sont eux-mêmes héréditairement finis) et une arête relie deux sommets lorsque l'un d'eux est élément de l'autre[4].

Une autre construction du graphe de Rado est analogue à celle des graphes de Paley. Les sommets sont les nombres premiers de la forme 4n + 1, et une arête les relie si l'un des deux est résidu quadratique modulo l'autre (cette relation étant symétrique d'après la loi de réciprocité quadratique)[5].

On peut également le construire comme graphe d’intersection d'un système de blocs (en) infini où chaque bloc est infini (dénombrable)[6].

Propriétés

Propriété d'extension
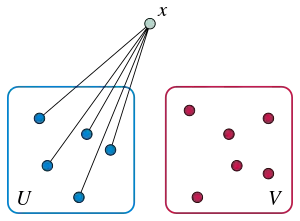
La propriété d'extension : pour tout couple d'ensembles de sommets finis disjoints U et V, il existe un sommet x relié à tous les sommets de U, et à aucun de ceux de V.

Le graphe de Rado satisfait la propriété d'extension suivante[2] : pour tout couple d'ensembles de sommets finis disjoints U et V, il existe un sommet x n'appartenant ni à U, ni à V, et connecté à tous les sommets de U, mais à aucun de ceux de V ; cette propriété caractérise ce graphe, comme montré ci-dessous.

La définition du graphe par représentation binaire en permet une démonstration constructive, en posant

 :

x est par construction plus grand que tous les éléments de U et de V, adjacent à tous les éléments de U, et puisque U et V sont disjoints, x n'est adjacent à aucun élément de V[alpha 1].

La construction comme graphe aléatoire donne à chaque sommet non dans U ou V une probabilité p|U|(1-p)|V| de satisfaire la propriété d'extension, indépendamment des autres sommets ; comme il y a une infinité de tels sommets, il y en a presque sûrement un satisfaisant la propriété[2].

Sous-graphes

Pour tout graphe fini ou infini dénombrable G, la propriété d'extension permet de construire un sous-graphe du graphe de Rado isomorphe à G. La démonstration se fait par récurrence sur les sommets de G (supposés indexés par les entiers) : supposant construit un isomorphisme pour les n premiers sommets, on ajoute un nouveau sommet en choisissant dans le graphe de Rado un sommet ayant exactement les mêmes liens avec les sommets déjà construits que les sommets correspondants dans G[7]. Pour cette raison, on dit parfois que le graphe de Rado est un graphe universel[8], mais il s'agit en fait d'une notion plus faible que celle de problème universel, définie par la théorie des catégories.

Unicité

Le graphe de Rado est, à isomorphisme près, le seul graphe dénombrable ayant la propriété d'extension. En effet, si G et H sont deux graphes ayant cette propriété, chacun des deux est isomorphe à un sous-graphe de l'autre ; précisant la construction de ces sous-graphes, il est possible d'obtenir par récurrence un isomorphisme entre G et H en utilisant la méthode du va-et-vient (de façon analogue à la démonstration du théorème de Cantor-Bernstein)[9].

Symétries

Partant de deux sous-graphes du graphe de Rado finis et isomorphes, la construction précédente permet de prolonger cet isomorphisme en un automorphisme du graphe entier ; on dit que le graphe de Rado est ultrahomogène[9]. En particulier, il existe un automorphisme envoyant deux arêtes quelconques l'une sur l'autre, et le graphe de Rado est donc un graphe symétrique. Le groupe des automorphismes du graphe de Rado est un groupe simple ayant la puissance du continu[10].

Partitions

Toute partition finie des sommets du graphe de Rado induit au moins un sous-graphe isomorphe au graphe entier. Cameron 2001 en donne une preuve courte, obtenue en recollant des sous-ensembles de chaque sous-graphe induit qui ne vérifieraient pas la propriété d'extension. Trois graphes non-orientés dénombrables seulement ont cette propriété : le graphe de Rado, le graphe complet, et le graphe vide[11]. Bonato, Cameron et Delić 2000 et Diestel et al. 2007 ont montré que les seuls graphes orientés ayant la même propriété sont obtenus à partir de ces trois graphes en choisissant des orientations convenables des arêtes.

Si l'on s'intéresse à des partitions des arêtes, un résultat analogue, mais plus faible, montre qu'il existe un sous-graphe isomorphe au graphe de Rado entier en choisissant les arêtes parmi deux des éléments de la partition, mais que ce n'est pas toujours possible de prendre les arêtes dans un seul élément[12].

Relation avec la théorie des modèles

Ronald Fagin a démontré que si un énoncé concernant les graphes (plus rigoureusement un énoncé de la théorie égalitaire du premier ordre contenant la relation d'adjacence , qui exprime qu'une arête relie les sommets a et b) est vrai pour le graphe de Rado, il est vrai pour presque tous les graphes finis, c'est-à-dire que la proportion des graphes à n sommets pour lesquels l'énoncé est vrai tend vers 1 lorsque n tend vers l'infini[13].

La propriété d'extension peut être exprimée par une suite infinie d'énoncés du premier ordre , l'affirmant pour tous les ensembles de sommets U et V ayant respectivement i et j éléments[14]. Par exemple, peut s'écrire comme

Haim Gaifman (en) a démontré[15] que l'ensemble des et des énoncés affirmant que la relation d'adjacence est symétrique et antiréflexive sont les axiomes d'une théorie complète[16], dont le graphe de Rado est l'unique modèle dénombrable (ce dernier résultat découle de l'unicité des graphes possédant la propriété d'extension, et permet de démontrer la complétude grâce au critère de Łoś–Vaught[17]).

Généralisations

La propriété universelle du graphe de Rado ne se généralise pas, par exemple, à des plongements isométriques, c'est-à-dire à des isomorphismes conservant la distance : le graphe de Rado est de diamètre deux, et donc aucun graphe de diamètre supérieur ne peut s'y plonger isométriquement. Moss a construit pour chaque valeur de n un graphe contenant isométriquement tous les graphes finis de diamètre n[18], obtenant le graphe infini complet pour n = 1 et le graphe de Rado pour n = 2.

Saharon Shelah a étudié l'existence de graphes universels non dénombrables, obtenant des conditions d'existence suffisantes sur leur cardinal[19].

Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Rado graph » (voir la liste des auteurs).

Notes
  1. Une construction essentiellement équivalente, mais donnée en termes ensemblistes, constitue le théorème 2 de Cameron 1997.

Références
  1. Ackermann 1937 ; Rado 1964.
  2. Voir Cameron 1997, résultat 1.
  3. Cameron 1997, proposition 5.
  4. Cameron 1997, théorème 2.
  5. Cameron 1997.
  6. Horsley, Pike et Sanaei 2011.
  7. Cameron 1997, proposition 6.
  8. Delahaye 2018
  9. Cameron 2001.
  10. Cameron 1997, section 1.8 : le groupe des automorphismes.
  11. Cameron 1990 ; Diestel et al. 2007.
  12. Pouzet et Sauer 1996.
  13. Fagin 1976.
  14. Spencer 2001, section 1.3, "Extension Statements and Rooted Graphs", p. 17-18.
  15. Gaifman 1964.
  16. Gaifman 1964 ; Marker 2002, théorème 2.4.2, p. 50.
  17. Marker 2002, théorème 2.2.6, p. 42.
  18. Moss 1989.
  19. Shelah 1984.

Bibliographie
  • Portail des mathématiques
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.