Fonction de transfert optique
La fonction de transfert optique ou FTO d'un système optique est une fonction complexe qui relie la luminance de l'espace objet à l'éclairement de l'espace image. Elle permet de modéliser l'influence du système optique sur la distribution de l'énergie lumineuse dans l'espace image.

La fonction de transfert optique est souvent considérée uniquement dans les plans objets et images conjugués mais est tridimensionnelle dans le cas général. Cette fonction complexe est décomposée en une amplitude dite fonction de transfert de modulation et une phase dite fonction de transfert de phase.
- La fonction de transfert de modulation ou FTM est une fonction qui permet de caractériser la capacité du système optique à restituer du contraste en fonction de la finesse des détails de l'objet ; autrement dit, sa capacité à transmettre les fréquences spatiales de l'objet. Elle est utilisée pour évaluer la qualité du système optique, notamment en photographie et cinématographie.
- La fonction de transfert de phase caractérise les déphasages introduits par le système optique. Elle intervient surtout en champ proche, dans l'hypothèse d'une diffraction de Fresnel[1].
La notion de fonction de transfert optique possède des analogues dans d'autres domaines de la physique, notamment en électronique et en acoustique.
Définition

Le système optique forme l'image d'un objet plan dans le plan image.
On désigne par :
- la distribution de l'exitance dans la direction de la pupille d'entrée du système optique dans le plan objet ;
- la fonction d'étalement du point (« point spread function » en anglais), ou réponse impulsionnelle spatiale, c'est-à-dire la répartition de l'éclairement pour un point lumineux objet située en ;
- la distribution de l'éclairement reçu dans le plan image.
Moyennant quelques hypothèses, parmi lesquelles l'invariance du système optique et l'incohérence de la lumière émise par la source, on peut les mettre en relation de la façon suivante et faire apparaître un produit de convolution[2] :
- ,
- .
Dans ce cas, si on effectue un transformation de Fourier, on peut écrire
où
- et sont les fréquences spatiales verticales et horizontales de l'image formée ;
- et sont les fréquences spatiales verticales et horizontales de l'objet ;
- représente la répartition de l'éclairement en fonction des fréquences spatiales ;
- représente la répartition de l'exitance en fonction des fréquences spatiales ;
- est la fonction de transfert optique[2],[3],[4] (FTO) : il s'agit dans ce cas de la transformée de Fourier de la fonction d'étalement du point.
Cette fonction peut être réécrite pour faire intervenir un terme d'amplitude et un terme de phase selon où :
- est la fonction de transfert de modulation (FTM, ou « modulation transfert function », MTF, en anglais), module de la FTO ;
- est la fonction de transfert de phase (FTP), argument de la FTO.
La fonction de transfert optique normalisée présente une valeur unité pour les fréquences spatiales nulles.
Extension de la FTM au cas tridimensionnel
La fonction d'étalement du point d'un système optique, c'est-à-dire l'image d'un point objet, est une distribution d'éclairement à trois dimensions présentant un maximum dans le plan conjugué du plan objet. Il est donc possible de définir une fonction de transfert optique tridimensionnelle et la fonction de transfert de modulation associée[5].
Système optique limité par la diffraction
Il est utile de connaître le comportement d'un système optique idéal, dans le sens où il est dépourvu d'aberration, afin de le comparer à un système optique réel. En pratique, un système est dit limité par la diffraction si les aberrations qui l'affectent ont une fonction d'étalement du point plus petite que la tache d'Airy créée par la diffraction. La fonction d'étalement du point est obtenu correspond, à un changement de variable près, à la transformée de Fourier en deux dimensions de la forme de l'ouverture :
- ,
Alors la fonction de transfert optique s'exprime très simplement comme le produit de d'autocorrélation de la forme de l'ouverture :
où est le grandissement transversal.
Les fréquences maximales enregistrées par le système imageant sont soit limitées par le système optique par effet de diffraction, soit par le capteur à cause de la taille des pixels par exemple[6]. Dans de nombreux cas, si l'objet est suffisamment éloigné, on considère que l'image se forme au voisinage du plan focal de sorte que .
Ouverture circulaire

Dans le cas d'un système optique de distance focale image et muni d'une pupille d'entrée d'ouverture circulaire de diamètre , le nombre d'ouverture est notée . On considère également que l'image se forme au voisinage du plan focal : . La symétrie du problème permet d'exprimer la fonction de transfert optique normalisée en fonction des fréquences spatiales selon n'importe quel axe radial de l'ouverture :
- ,
où la fréquence de coupure, au-delà de laquelle il n'y a plus aucun contraste, est donnée par : .
Ouverture carrée
Dans le cas d'une ouverture carrée de côté , le facteur de transmission est :
- ,
où représente la fonction porte. Le nombre d'ouverture étant encore définie comme , la fréquence de coupure garde la même expression, mais la fonction de transfert optique est modifiée :
- ,
où est la fonction triangle.
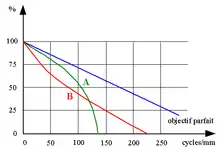
Système optique réel
Un système réel souffre d'aberrations optiques. L'effet de ces aberrations est de réduire le taux de contraste en fonction des fréquences spatiales, ce qui se traduit par une baisse de la FTM par rapport au cas limité par la diffraction[7]. Cette baisse du contraste peut s'accompagner d'une diminution de la fréquence de coupure du système optique, information indispensable permettant de déterminer la capacité d'un système à transmettre les détails fins d'une image[8]. Les aberrations optiques qui dégradent la performance des systèmes ne sont pas invariantes spatialement ce qui interdit l'utilisation du produit de convolution et réduit les possibilités de calculs simples. De plus, elles ne sont pas toutes à symétrie de rotation. Alors, la fonction de transfert optique n'est pas à symétrie de rotation et en particulier la FTM varie suivant la position étudiée dans le plan image. Pour connaître la FTM, il est nécessaire de procéder à des mesures.
Mesure de la FTM

Méthodes utilisant des mires

La fonction de transfert de modulation peut être mesurée à l'aide de mires constituées de bandes noires et blanches alternant à différentes fréquences spatiales[9]. Pour chaque fréquence spatiale, le contraste est mesuré sur l'image et divisé par le contraste de la mire.
- [10],
avec et les luminances minimales et maximales mesurées sur l'image de la mire. Ce rapport est la valeur de la fonction de transfert de modulation pour cette fréquence spatiale.
Méthodes de mesure directe
Si le détecteur a une résolution suffisante et qu'une source lumineuse de taille suffisamment petite peut être utilisée, il est possible de mesurer directement la fonction d'étalement du point du système optique[11]. La fonction d'étalement du point permet ensuite de calculer la fonction de transfert de modulation par une transformation de Fourier.
Alternativement, en l'absence de détecteur, une mesure de la baisse de l'intensité lumineuse en présence d'un couteau de Foucault permet de calculer la fonction de transfert de modulation. Cette méthode est souvent utilisée dans les domaines où les capteurs ne disposent pas d'une résolution suffisante, comme pour l'infrarouge.
Méthodes utilisant des analyseurs de front d'onde
L'utilisation d'un analyseur de front d'onde permet d'analyser la déformation du front d'onde par un système optique. En particulier, de tels systèmes permettent de mesurer la réponse impulsionnelle d'un système optique. La fonction de transfert optique étant la transformée de Fourier de cette réponse impulsionnelle, il est ainsi possible d'obtenir la fonction de transfert de modulation[12],[13].

Facteurs influençant la FTM
La FTM d'un système optique dépend évidemment de l'ouverture et de sa forme, ainsi que de la longueur d'onde du fait de la diffraction, mais d'autres phénomènes interviennent pour la dégrader.
La plupart des aberrations géométriques et chromatiques qui affectent le système optiques, en plus des défauts de fabrication ou de soin, réduisent la les valeurs de la FTM : aberration sphérique, aberration de coma, astigmatisme, courbure de champ, trèfle. Les réflexions internes au système optique peuvent réduire la FTM sur la totalité de l'image par diminution du contraste par effet de flare. Le vignettage et la distorsion n'ont pas d'influence sur la FTM. Les aberrations chromatiques n'ont pas d'influence en lumière quasi-monochromatique. La distance à l'objet peut changer les aberrations optiques présentes dans le système optique et modifier la FTM associée à celui-ci. La polarisation de la lumière incidente peut, plus rarement, avoir une influence.

Utilisation en Photographie et Cinéma
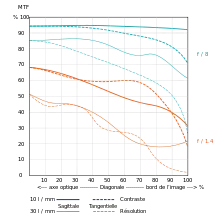
La fonction de transfert de modulation permet de caractériser la qualité d'un objectif.
Courbe de FTM en photographie
Les courbes de FTM caractérisant un objectif photographique comportent au moins deux courbes[14],[15]:
- La courbe supérieure correspond à l'évolution du contraste d'une fréquence spatiale faible (souvent 10 cycles par millimètre) en fonction de la distance au centre de l'image.
- La courbe inférieure correspond à l'évolution du contraste d'une fréquence spatiale plus élevée (souvent 30 cycles par millimètre) en fonction de la distance au centre de l'image.
Ces courbes sont dédoublées en fonction de l'orientation sagittale ou tangentiel, permettant de rendre compte d'aberrations n'ayant pas de symétrie de rotation[16].
Les objectifs photographiques présentent une FTM maximale pour les ouvertures moyennes (f/5,6). La FTM est plus faible pour les grandes ouvertures (f/1,4, f/2) du fait des aberrations, et pour les petites ouverture du fait de la diffraction. Les fabricants d'objectifs limitent généralement l'ouverture à f/16 ou f/22 (f/32 pour les grands formats). La diffraction affecte moins les grands capteurs (à définition égale) car les pixels sont plus grands et que la taille de la tache de diffraction ne dépend que de l'ouverture.
Notions analogues à la fonction de transfert optique
En électronique
En électronique, la notion de fonction de transfert d'un circuit électrique est en particulier utilisée pour analyser la réponse en fréquence du système, qui correspond au gain du système en fonction de la fréquence du signal électrique en entrée. Il est possible de faire l'analogie entre fonction de transfert optique et fonction de transfert d'une part et entre fonction de transfert de modulation et réponse en fréquence d'autre part.
En acoustique
En acoustique, la fonction de transfert de modulation est utilisée pour évaluer comment les modulations en amplitude du signal sont affectées au cours de la diffusion d'un signal. La fonction de transfert de modulation pour un signal à bande étroite est calculée par le rapport des contrastes (signal modifié - signal d'origine) pour des modulations d'amplitude allant de 1 à 12 Hz. La FTM est à la base de plusieurs mesures d'intelligibilité de la parole et en particulier du Speech Transmission Index (STI)[17].
Voir aussi
Notes et références
- Le champ proche optique: Théorie et applications sur Google Livres - Daniel Courjon et Claudine Bainier (2001)
- Eugene Hecht, Optique, Pearson, , 724 p. (ISBN 978-2-7440-7063-1, lire en ligne), p. 571
- Thèse : Analyse et modélisation de la fonction de transfert de modulation des capteurs d'images à pixels actifs CMOS - Magali Estribeau (2004)
- Norme ISO 15529 révision 2010
- Fast vectorial calculation of the volumetric focused field distribution by using a three-dimensional Fourier transform - J. Lin, O. G. Rodríguez-Herrera, F. Kenny, D. Lara, and J. C. Dainty, Optics Express (2012)
- Éléments de Conception Optique (lire en ligne), p. 8
- Formation, Capture et Restitution des images p. 78 - Jean-Louis Meyzonnette, Ecole Supérieure d’Optique
- (en) Glenn D. Boreman, Modulation Transfer Function in Optical and Electro-optical Systems, SPIE Press, , 110 p. (ISBN 978-0-8194-4143-0, lire en ligne), p. 16
- Introduction to Optical Testing sur Google Livres - Joseph M. Geary
- Documentation MTF - Imatest
- Mesure de la Fonction de Transfert de Modulation d’un système optique - Travaux Pratiques, Institut d'Optique
- Capteur de front d'onde HASO - Imagine Optic
- Analyseur de front d'onde Shack-Hartmann - OptoPhase
- The Interpretation of Optical Data Sheets - Carl Zeiss
- Comprendre la fonction de transfert de modulation - FocusNumérique
- Comment lire les courbes de MTF - Sigma France
- Introducing speech intelligibility nti-audio.com
- Portail de la photographie
- Portail de l’optique
