Cube Soma

Le cube Soma est un casse-tête mécanique inventé dans les années 1930 par le poète et scientifique danois Piet Hein.

Cube Soma
casse-tête

Le cube assemblé.

Données clés
Auteur	Piet Hein
Date de 1^re édition	année 1930
Durée annoncée	variable

Données clés
habileté physique Non	réflexion décision Oui	générateur de hasard Non	info. compl. et parfaite

Les différentes pièces à assembler pour reconstituer le cube.

Principe

Le casse-tête est constitué de sept pièces différentes, chacune formée d'un certain nombre de cubes unitaires. Le but du jeu est d'assembler ces pièces de manière à former un cube de trois unités de côté. Les pièces peuvent aussi être combinées en une grande variété d'autres motifs.

Ce puzzle est souvent considéré comme l'équivalent en trois dimensions des polyominos.

Histoire

Selon la légende rapportée en 1958 par Martin Gardner[1], ce casse-tête aurait été inventé par Hein en 1936, pendant un cours de mécanique quantique donné par Werner Heisenberg. Néanmoins, Ole Poul Pedersen a trouvé en 2003[2] un brevet danois déposé par Hein dès le 2 décembre 1933[3], suivi par un brevet britannique déposé le 20 mars 1934[4], soit plusieurs années avant la date avancée pour le cours d'Heisenberg[5].

Le nom, Soma, est peut-être tiré du roman d'Aldous Huxley, Le Meilleur des mondes[6]^,[7]. Ce roman décrit une société du futur dans laquelle le Soma est une drogue addictive, grâce à laquelle chaque élément de la société est heureux et ne revendique rien.

Détail des sept pièces du cube

Les éléments du cube Soma sont formés de toutes les combinaisons possibles de quatre cubes unitaires ou moins, à l'exception des formes convexes (i.e., les cuboïdes 1×1×1, 1×1×2, 1×1×3, 1×1×4 et 1×2×2). Il reste donc seulement un tricube (pièce composée de 3 cubes unitaires) et six tétracubes (pièces composées de 4 cubes unitaires), deux d'entre eux formant une paire d'énantiomères.

tricube
tétracube L
tétracube T
tétracube S
tétracube
(vis directe)
tétracube
(vis rétrograde)
tétracube
(branches)

Solutions

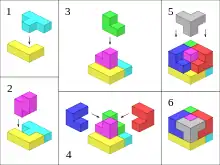
Un des assemblages possibles du cube Soma.

Le cube Soma a été étudié en détail par Martin Gardner et John Horton Conway. Le livre Winning Ways for your Mathematical Plays contient une analyse du problème[8]. Il y a 240 solutions distinctes pour reconstituer le cube. Ces solutions peuvent être facilement générées par un ordinateur à l'aide d'un algorithme récursif comme celui de retour sur trace[9].

Le record du monde de vitesse pour résoudre un cube soma a été établi par Krishnam Raju Gadiraju (en) de Bangalore en Inde[10]^,[11] : le 19 octobre 2017, il a reconstitué le cube en 2,93 secondes[12].

Utilisations en psychologie

Le cube Soma a été utilisé dans des expériences de psychologie. Par exemple, à l'été 1969, Edward Deci (en), alors étudiant en cycle graduate à l'université Carnegie-Mellon, a demandé à des étudiants de résoudre un cube Soma avec ou sans récompense, dans son sujet d'étude sur les mécanismes de motivation intrinsèque et extrinsèque[13]^,[14]^,[15]. Il a également été utilisé en 1976 par Teresa Amabile (en), William DeJong (en) et Mark Lepper (en)[16].

Notes et références

(en) Martin Gardner, « Mathematical Games : A Game in Which Standard Pieces Composed of Cubes are Assembled into Larger Forms », Scientific American, n^o 199,‎ septembre 1958, p. 182–192.
(en) Thorleif Bundgaard, « SOMA News: The birth of SOMA ? », sur Thorleif's SOMA page, 10 mars 2003.
(da) « Sammenlægnings- eller Puslespil med ikke- kasseformede Klodser », brevet danois n^o 52215, déposé le 2 décembre 1933, protégé le 15 septembre 1936, publié le 28 septembre 1936 ; reproduit sur Espacenet, Office européen des brevets.
(en) « Toy Building or Puzzle Blocks », brevet britannique n^o 420,349, déposé le 20 mars 1934, publié le 29 novembre 1934 ; reproduit sur Espacenet, Office européen des brevets.
Jean-Paul Delahaye, « Les 27 petits cubes de Piet Hein », Pour la science, n^o 382,‎ août 2009, p. 80 (résumé).
(en) Martin Gardner, The Second Scientific American Book of Mathematical Puzzles & Diversions, New York, Simon & Schuster, 1961, 254 p. (ISBN 0-226-28253-8), chap. 6 (« The Soma Cube »), p. 65–77 : au début du chapitre est mise en exergue une citation du roman évoquant la drogue Soma.
(en) David J. Darling, The Universal Book of Mathematics : From Abracadabra to Zeno's Paradoxes, Hoboken, John Wiley & Sons, 2004, 383 p. (ISBN 0-471-27047-4), p. 295–296.
(en) Elwyn Berlekamp, John Conway et Richard Guy, Winning Ways for your Mathematical Plays, vol. 2 : Games in Particular, New York, Academic Press, 1982 (ISBN 0-12-091152-3 et 0-12-091102-7), p. 735.
(en) Jay P. Fillmore et S. G. Williamson, « On Backtracking: A Combinatorial Description of the Algorithm », SIAM Journal on Computing, vol. 3, n^o 1,‎ mars 1974, p. 41–55 (DOI 10.1137/0203004).
(en) Deepika Burli, « He can solve Rubik’s Cube underwater », The Times of India, 13 novembre 2017.
(en) Akhila Damodaran, « Bangalore boy becomes first Indian to set record in speed solving, unicycling », The New Indian Express, 6 novembre 2018.
(en) « Fastest time to complete a Soma cube », Guinness World Record.
(en) Daniel Pink, Drive : The Surprising Truth about what Motivates Us, New York, Riverhead Books, 2009, 242 p. (ISBN 978-1-59448-884-9), p. 5–9 ; Daniel Pink (trad. de l'anglais par Marc Rozenbaum), La vérité sur ce qui nous motive : Tout ce qu’il faut savoir pour transformer sa vie et aller de l’avant !, Paris, Leduc.s, coll. « Business », 2011, 245 p. (ISBN 978-2-84899-454-3), p. 15–19.
(en) Edward Deci, « Effects of externally mediated rewards on intrinsic motivation », Journal of Personality and Social Psychology, vol. 18, n^o 1,‎ avril 1971, p. 105–115 (DOI 10.1037/h0030644).
(en) Edward Deci, « Intrinsic motivation, extrinsic reinforcement, and inequity », Journal of Personality and Social Psychology, vol. 22, n^o 1,‎ avril 1972, p. 113–120 (DOI 10.1037/h0032355).
(en) Teresa Amabile, William DeJong et Mark Lepper, « Effects of externally imposed deadlines on subsequent intrinsic motivation », Journal of Personality and Social Psychology, vol. 34, n^o 1,‎ 1976, p. 92–98 (DOI 10.1037/0022-3514.34.1.92).

Lien externe

(en) Eric W. Weisstein, « Soma Cube », sur MathWorld

Portail des jeux
Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Martin Gardner, « Mathematical Games : A Game in Which Standard Pieces Composed of Cubes are Assembled into Larger Forms », Scientific American, n^o 199,‎ septembre 1958, p. 182–192.

[2] (en) Thorleif Bundgaard, « SOMA News: The birth of SOMA ? », sur Thorleif's SOMA page, 10 mars 2003.

[3] (da) « Sammenlægnings- eller Puslespil med ikke- kasseformede Klodser », brevet danois n^o 52215, déposé le 2 décembre 1933, protégé le 15 septembre 1936, publié le 28 septembre 1936 ; reproduit sur Espacenet, Office européen des brevets.

[4] (en) « Toy Building or Puzzle Blocks », brevet britannique n^o 420,349, déposé le 20 mars 1934, publié le 29 novembre 1934 ; reproduit sur Espacenet, Office européen des brevets.

[5] Jean-Paul Delahaye, « Les 27 petits cubes de Piet Hein », Pour la science, n^o 382,‎ août 2009, p. 80 (résumé).

[6] (en) Martin Gardner, The Second Scientific American Book of Mathematical Puzzles & Diversions, New York, Simon & Schuster, 1961, 254 p. (ISBN 0-226-28253-8), chap. 6 (« The Soma Cube »), p. 65–77 : au début du chapitre est mise en exergue une citation du roman évoquant la drogue Soma.

[7] (en) David J. Darling, The Universal Book of Mathematics : From Abracadabra to Zeno's Paradoxes, Hoboken, John Wiley & Sons, 2004, 383 p. (ISBN 0-471-27047-4), p. 295–296.

[8] (en) Elwyn Berlekamp, John Conway et Richard Guy, Winning Ways for your Mathematical Plays, vol. 2 : Games in Particular, New York, Academic Press, 1982 (ISBN 0-12-091152-3 et 0-12-091102-7), p. 735.

[9] (en) Jay P. Fillmore et S. G. Williamson, « On Backtracking: A Combinatorial Description of the Algorithm », SIAM Journal on Computing, vol. 3, n^o 1,‎ mars 1974, p. 41–55 (DOI 10.1137/0203004).

[10] (en) Deepika Burli, « He can solve Rubik’s Cube underwater », The Times of India, 13 novembre 2017.

[11] (en) Akhila Damodaran, « Bangalore boy becomes first Indian to set record in speed solving, unicycling », The New Indian Express, 6 novembre 2018.

[12] (en) « Fastest time to complete a Soma cube », Guinness World Record.

[13] (en) Daniel Pink, Drive : The Surprising Truth about what Motivates Us, New York, Riverhead Books, 2009, 242 p. (ISBN 978-1-59448-884-9), p. 5–9 ; Daniel Pink (trad. de l'anglais par Marc Rozenbaum), La vérité sur ce qui nous motive : Tout ce qu’il faut savoir pour transformer sa vie et aller de l’avant !, Paris, Leduc.s, coll. « Business », 2011, 245 p. (ISBN 978-2-84899-454-3), p. 15–19.

[14] (en) Edward Deci, « Effects of externally mediated rewards on intrinsic motivation », Journal of Personality and Social Psychology, vol. 18, n^o 1,‎ avril 1971, p. 105–115 (DOI 10.1037/h0030644).

[15] (en) Edward Deci, « Intrinsic motivation, extrinsic reinforcement, and inequity », Journal of Personality and Social Psychology, vol. 22, n^o 1,‎ avril 1972, p. 113–120 (DOI 10.1037/h0032355).

[16] (en) Teresa Amabile, William DeJong et Mark Lepper, « Effects of externally imposed deadlines on subsequent intrinsic motivation », Journal of Personality and Social Psychology, vol. 34, n^o 1,‎ 1976, p. 92–98 (DOI 10.1037/0022-3514.34.1.92).