Courbure terrestre
La courbure terrestre — nommée aussi dépression — définit l'horizon visuel apporté par la rotondité ou sphéricité de la Terre. Elle limite la vision (théorique) lointaine par exemple sur la mer. Plus l'altitude du point d'observation, ou d'émission dans le cas des émetteurs de télévision ou FM, est élevée, plus la distance de vision est importante. On parle aussi de ligne d'horizon visuelle ou hertzienne.

C'est pour cette raison que très tôt les feux des phares ont été placés dans des positions aussi élevées que possible malgré l'augmentation de coût que cela impliquait dans leur construction, et que les hunes d'observation des navires étaient placées en haut du plus grand mât.
Dans le cas particulier des transmissions hertziennes terrestres, il faut en plus tenir compte des caractéristiques du point de réception vrai (altitude du lieu + hauteur des antennes, plus connu sous le nom de « cote Z »). Les 2 distances doivent être comptabilisées. Si on admet que la hauteur moyenne d'un râteau UHF est à 12 m du sol, le dégagement théorique est de 12,498 65 km.
Ceci est également valable pour les vues panoramiques agrémentées de hauts sommets, même réputés lointains.
Ces choix ont présidé au choix des sites du télégraphe de Chappe au XVIIIe siècle.
Première approche
| Altitude | Distance de l'horizon |
| 1,70 m | 4,7 km |
| 3,00 m | 6,2 km |
| 10 m | 11,3 km |
| 50 m | 25,4 km |
| 75 m | 31,1 km |
| 100 m | 36,0 km |
| 250 m | 56,9 km |
| 500 m | 80,4 km |
| 750 m | 98,5 km |
| 1 km | 113 km |
| 1,5 km | 139 km |
| 2 km | 160 km |
| 3 km | 197 km |
| 4 km | 227 km |
Le tableau ci-contre indique quelques distances pour la limite de vision (en bord de mer), en fonction de quelques hauteurs d'observation, et pour un point observé distant qui est situé à 0 mètre d'altitude (altitude zéro).
Par exemple : depuis le sommet du mont Blanc, la distance de la limite de vision approche les 250 km ; alors que, depuis le sommet de la tour Eiffel, cette distance serait proche de 63 km.
(On notera que, en fonction de la valeur retenue pour le rayon terrestre, les résultats obtenus peuvent être légèrement différents.)
La formule de calcul est simple : c'est celle de la puissance d'un point par rapport à un cercle.
En effet, on peut démontrer que, quel que soit le segment sécant mené d'un point P extérieur à un cercle de centre O, de rayon R et le coupant en des points A et B, on a : PA x PB = constante = PO² - R².
Le point limite de vision est le point situé sur la droite qui passe par le point P et qui est tangente à la Terre, cas particulier avec A = B.
Le rayon de la Terre étant de 6 371 km, on calcule facilement que (d étant la portée, et h étant la hauteur ; ces deux valeurs étant toutes deux exprimées en kilomètres).
Les points mutuellement visibles doivent avoir une altitude apparente qui soit supérieure à la hauteur vraie de l'obstacle s'élevant au-dessus de l'arc terrestre nominal. Un obstacle peu élevé, mais trop proche peut être plus pénalisant qu'un obstacle plus haut, mais plus éloigné du point d'observation ou de réception.
Ces valeurs théoriques sont fortement influencées par l'espace et les caractéristiques du relief, c'est-à-dire par l'altitude et situation des obstacles dans le trajet qui sépare les deux points considérés, ou géomorphologie ; la représentation intuitive étant la vue en coupe.
Ces valeurs théoriques sont également très fortement influencées par les conditions météorologiques (en particulier, et surtout, par la pollution), qui peuvent induire un phénomène de réfraction.
C'est ainsi que, par exemple, on peut observer une bonne partie du massif du Mont-Blanc depuis les 1 424 m du Grand Ballon dans les Vosges, ces montagnes étant pourtant éloignées de près de 230 km, et le trajet visuel passant au-dessus du massif du Jura suisse. Et c'est également ce phénomène de réfraction qui permet aux habitants de la Côte d'Azur et aux Monégasques, certains jours, d'apercevoir la côte montagneuse nord de la Corse. C'est aussi l'explication au fait que des Marseillais ont pu voir un mont (Pic du Canigou) des Pyrénées en ombre chinoise sur un soleil couchant au-dessus de la Méditerranée[1].
Pour voir en ligne droite (sans « couper la mer ») le sommet du Canigou depuis Marseille, il faut se trouver sur un point, du côté de la cité phocéenne, présentant une altitude de 300 m environ au-dessus du niveau de la mer, et même un peu moins du côté du cap Croisette.
Dans les transmissions, et notamment en télévision terrestre VHF et UHF, les diffuseurs ont donc intérêt à choisir un point haut pour ériger les émetteurs de télévision avec des fréquences les plus basses pour mieux desservir les angles morts (un peu sous la ligne de visée) situés « derrière » l'obstacle, colline, ou dans la dépression, et ainsi améliorer la zone de couverture.
Deuxième approche
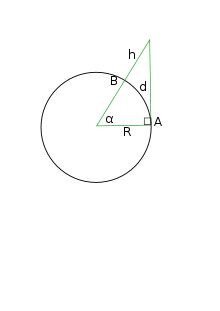
On peut calculer comment varie la courbure au fur et à mesure que l'on s'éloigne d'un point A, c'est-à-dire à quelle hauteur h se trouverait un rayon de lumière lancé à l'horizontale de A, vu depuis un point B distant sur terre de d = AB (d = distance courbe sur la sphère), qui est un arc de cercle, représentant un angle au centre α = d/R (note : pour d = π/2 R, on a bien α = π/2), la Terre étant une sphère de rayon R.
Dans ce cas on calcule :
.
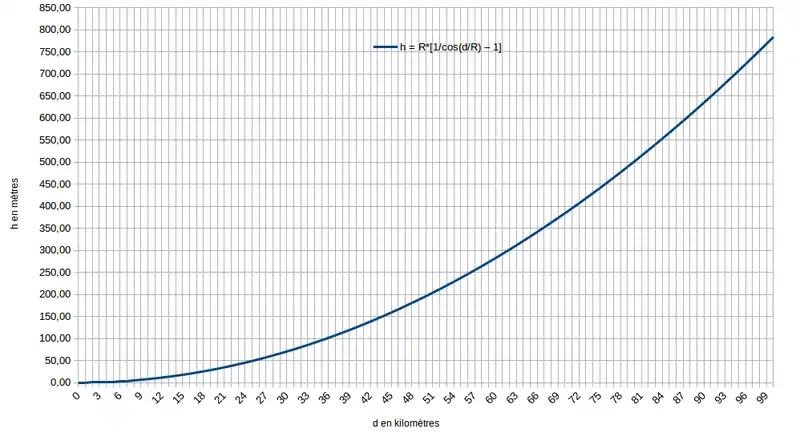
Avec R = 6 378 km on obtient donc, en fonction de la distance terrestre d'entre les points A et B, la hauteur attendue avec l'horizontale, par rapport à la courbure, qui est la même chose que la hauteur maximale en B d'un objet qui sera invisible depuis A :
Troisième approche

On calcule ici quelle sera la hauteur h2 cachée en B selon un observateur A placé à une distance (sur la sphère) de d = AB sur la sphère de rayon R.
On calcule la distance :
et donc on obtient :
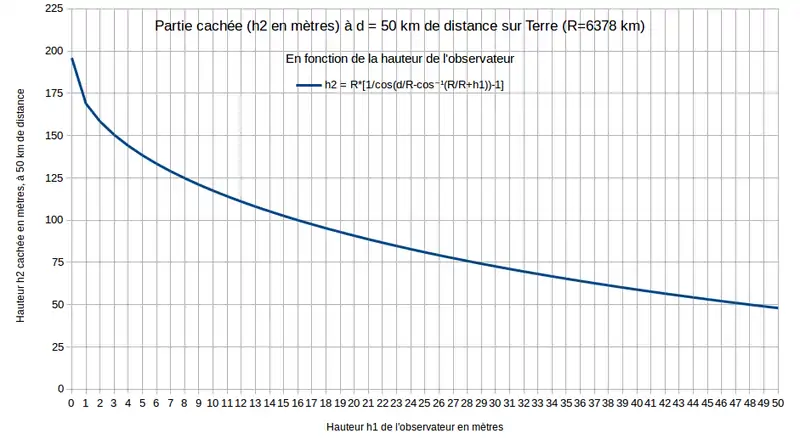
Avec R = 6 378 km et d = 50 km entre les deux points d'observation, on obtient alors selon la hauteur h1 de l'observateur une hauteur cachée qui décroît :
Quatrième approche
On calcule ici quelle sera la courbure de la ligne d'horizon que l'on verra sur une photographie, en fonction des caractéristiques de l'appareil photo, et de l'altitude à laquelle on se trouve.
La ligne d'horizon sera un cercle vu en perspective, autrement dit une conique. Il est relativement difficile de calculer l'équation de cette fonction[2]. Il sera plus simple de déterminer uniquement son élévation maximum.
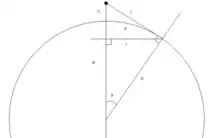
Le schéma ci-contre présente la terre de rayon avec un observateur situé à une altitude . On cherche à déterminer la distance de l'horizon et le rayon du cercle que forme cet horizon en fonction de l'altitude de l'observateur.
est le côté adjacent de dans le triangle , , , donc:
est le côté opposé de dans le triangle , , , donc:
est le côté opposé de dans le triangle rectangle d’hypoténuse , donc:
On déduit de et que
On déduit de et que
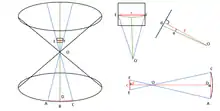
Sur le schéma ci-contre :
L'angle n'a plus la même signification que sur le schéma précédent (mais les autres désignations sont conservées).
L’horizon est le cercle de base du double cône, de rayon pour lequel on vient de déterminer un expression en fonction de et .
Le rectangle contenant E et F est le capteur de l’appareil photo.
Le sommet O du double cône est à la fois la position de l’observateur, et le centre optique de la lentille de distance focale qui sert à créer l’image de l’horizon.
L’arc AC est la portion d’horizon visible avec le système optique de longueur focale utilisant un capteur de largeur .
Le point B représente le point de l'horizon qui sera le plus élevé sur la photographie. Le rayon de lumière issu de ce point est représenté en vert sur le schéma ci-contre. Il forme avec l'axe optique de l'appareil photographie l'angle , que l'on retrouve de part et d'autre du centre optique O.
La distance à l'horizon pour laquelle on vient de déterminer une expression en fonction de et est égal à OA, OB et OC.
N.B. Cette construction n’est valable que si l’horizon occupe tout le capteur, autrement dit, si l'arc AC est inférieur ou égal au diamètre du cercle de base du cône.
Avec les calculs précédents, on a déterminé que et que
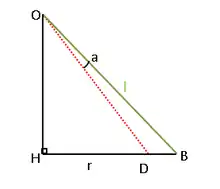
Dans les formules ci-dessus, est la longueur d’une génératrice du cône (OA, OB ou OC), et est le rayon de base de ce cône, représenté par HB sur la figure ci-contre.
On cherche à déterminer l'angle , car la tangente de cet angle est égal à la valeur de la dépression de l'horizon () divisé par la distance focale (), et par conséquent:
et par conséquent:
et par conséquent:
Or :
donc
Si on se place dans le plan des deux génératrices bleues FA et EC (du second schéma), on a :
Or, dans ce même plan :
et
Donc :
Et donc :
Par conséquent :
Si on reprend les expressions de découpage de l’angle , on peut alors effectuer le remplacement suivant:
et comme , on a alors:
Et si l'on remplace et dans cette expression, on obtient:
En ce qui concerne la condition de validité de ce calcule (le diamètre terrestre n'est pas intégralement visible dans l'image), elle se vérifie si
Or, on sait que :
Dans le triangle AOD on a :
Dans le triangle opposé à AOD contenant O, F et le centre du capteur photographique, on a pour l'angle opposé de même valeur:
Donc :
On remplace alors dans l’expression précédente de AD :
Or :
Donc :
On peut alors remplacer les expressions de AD et r dans celle de la condition initiale de validité des schémas utilisés, devient alors:
Voici la formule donnant courbure terrestre sur une photographie en fonction de l'altitude et des paramètres de l'appareil photo :
- est la dépression formée par la ligne d'horizon (son éloignement maximum par rapport à une ligne droite passant par les mêmes points sur les bords droite et gauche de l'image). Sur la photo présentée ci-dessus, représente la distance entre la ligne d'horizon de la mer, et la rambarde.
- est la distance focale de l'objectif utilisé, exprimé dans la même unité que et
- est la largeur du capteur de l'appareil photo utilisé. Comme ce calcul repose principalement sur les proportions, il est possible d'utiliser 36mm pour cette valeur, puis d'utiliser l'équivalent 24x36 pour la valeur de . Dans ce cas, sera obtenu en proportion de 24mm, on pourra alors faire une règle de trois pour convertir en pixels, en considérant que la hauteur de l'image correspond à 24mm.
- est la hauteur de l'hypoténuse du triangle rectangle présenté dans la deuxième approche, qui est également le rayon du cercle que forme la ligne d'horizon pour l'observateur. Il s'exprime de la façon suivante :
- est le côté opposé à l'angle α dans le triangle présenté dans le deuxième approche, c'est aussi la distance en ligne droite entre l'observateur et sa ligne d'horizon. Elle s'exprime de la façon suivante :
- est le rayon terrestre, exprimé dans la même unité que
- est l'altitude l'observateur, exprimé dans la même unité que
Cette formule a été déterminée en prenant les hypothèses suivantes :
- La terre est une sphère parfaite de rayon . Dans la réalité, la géodésie nous apprend que cette hypothèse n'est qu'une approximation de la réalité. Par exemple, avec une GoPro (focale équiv 24x36 de 17,2mm), il faudra être à plus de 2250m d'altitude pour que la dépression de l'horizon sur une sphère parfaite soit plus haute sur l'image qu'une montagne de 2000 mètres située à la même distance que cet horizon (169 km). Si on considère que l'horizon peut être confondu avec des nuages, pouvant monter jusqu'à 21 kilomètres d'altitude, avec cette même caméra, il faudra se placer à plus de 23,5 kilomètres au-dessus du sol pour que la dépression due à la courbure de l'horizon soit supérieure à la taille d'un cumulonimbus situé à la même distance que cet horizon (soit 547 kilomètres).
- L'appareil photo utilisé est un modèle simplifié semblable à un sténopé. Cette approximation est relativement juste si l'horizon passe par le centre de l'image. Si ce n'est pas le cas, les distorsions de l'objectif déformeront également la ligne d'horizon visible sur l'image. Cette déformation se fera toujours du centre de l'image vers l'extérieur de celle-ci. Ainsi, un horizon au-dessus du centre de l'image sera déformé vers le haut, et un horizon situé au-dessous sera déformé vers le bas.
- Le diamètre terrestre n'est pas entièrement visible dans l'image. Pour vérifier cela, il faut s'assurer, avant d'utiliser ce calcul, que :
Voici un exemple de résultats obtenus avec ce calcul, pour , , pour 3000 pixels et une hauteur du capteur photo de 24mm pour 2000 pixels :
| Altitude de l'observateur () | 0 | 17m | 100m | 400m | 800m | 1000m | 2km | 3km | 4km | 8km | 10km | 30km |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dépression de l'horizon () en pixels | 0 | 1 | 2 | 4 | 6 | 7 | 11 | 13 | 15 | 22 | 24 | 42 |
Voir aussi
- Rotation de la Terre
- Horizon (physique)
- Zone de couverture des ondes radio
Notes et références
- Michel Aperio, « Le Massif du Canigou vu de Marseille n'est pas une galéjade », www.univ-mrs.fr (consulté le ).
- (en) « Advanced Earth Curvature Calculator », sur http://walter.bislins.ch/bloge/, (consulté le )
- Portail de la géodésie et de la géophysique