Intégrale de Darboux

En analyse réelle, une branche des mathématiques, l'intégrale de Darboux est construite avec les sommes de Darboux et est une des définitions de l'intégrale d'une fonction. Les intégrales de Darboux sont équivalentes aux intégrales de Riemann, ainsi une fonction est Darboux-intégrable si et seulement si elle est Riemann-intégrable, et sont égales si elles existent toutes les deux[1]. La définition de l'intégrale de Darboux a l'avantage d'être plus simple à implémenter dans les calculs ou les preuves que l'intégrale de Riemann. Par conséquent, les manuels d'introduction en analyse développent l'intégrale de Riemann à partir de celle de Darboux, au lieu de la véritable intégrale de Riemann[2]. De plus, la définition est facilement extensible vers l'intégration de Riemann-Stieltjes[3]. Les intégrales de Darboux portent le nom de leur inventeur, Gaston Darboux.

Définition

La définition de l'intégrale de Darboux considère les intégrales (de Darboux) supérieure et inférieure, bien définies pour toute fonction à valeurs réelles bornée $f$ sur l'intervalle $[a, b]$ . L'intégrale de Darboux existe si et seulement si les intégrales inférieure et supérieure sont égales. Les intégrales inférieure et supérieure sont les limites respectives des sommes de Darboux inférieure et supérieure qui sous-estiment ou sur-estiment l'aire sous la courbe. Plus concrètement, pour une partition de l'intervalle donnée, les sommes de Darboux représentent la somme des aires des tranches rectangulaires dont les hauteurs sont prises respectivement aux suprema et aux infima de $f$ sur chaque sous-intervalle de la partition.

Sommes de Darboux

Pour la partition de l'intervalle $(x i)$ de l'intervalle $[a, b]$

a=x_{0}<x_{1}<\cdots <x_{n}=b.

Chaque intervalle $[x i -1, x i]$ est appelée un sous-intervalle de la partition. Soit $f : [a, b] \to R$ une fonction bornée, et soit

P=(x_{0},\ldots ,x_{n})

une partition de $[a, b]$ . Soit

M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x),m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x).

Sommes de Darboux inférieure (en vert) et supérieure (verte et grise) sur quatre sous-intervalles.

La somme de Darboux supérieure de $f$ selon $P$ est

U_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})M_{i}.\,\!

La somme de Darboux inférieure de $f$ selon $P$ est

L_{f,P}=\sum _{i=1}^{n}(x_{i}-x_{i-1})m_{i}.\,\!

Par abus, on les désigne plus simplement comme les sommes supérieur et inférieure.

Intégrales de Darboux

L'intégrale de Darboux supérieure de $f$ est

U_{f}=\inf\{U_{f,P}\colon P{\text{ est une partition de }}[a,b]\}.\,\!

L'intégrale de Darboux inférieure de $f$ est

L_{f}=\sup\{L_{f,P}\colon P{\text{ est une partition de }}[a,b]\}.\,\!

Dans certains ouvrages, un symbole intégral souligné ou surligné représentent les intégrales de Darboux inférieure et supérieure :

{\begin{aligned}L_{f}\equiv {\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\\[6pt]U_{f}\equiv {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x,\end{aligned}}

et le même abus de langage fait sur les sommes de Darboux peut être fait sur les intégrales.

Si $U f = L f$ , alors cette valeur commune est appelée intégrale de Darboux[4]. On dit alors que $f$ est Darboux-intégrable ou simplement intégrable et on pose

\int _{a}^{b}{f(t)\,\mathrm {d} t}=U_{f}=L_{f},

Un critère équivalent et parfois utile pour l'intégrabilité de $f$ est de montrer que pour tout $ε > 0$ il existe une partition $P ε$ de $[a, b]$ telle que[5]

U_{f,P_{\epsilon }}-L_{f,P_{\epsilon }}<\varepsilon .

Propriétés

Bornes

Pour toute partition donnée, la somme de Darboux est toujours supérieure ou égale à la somme de Darboux inférieure. De plus, la somme de Darboux inférieure est minorée par le rectangle de largeur (b−a) et de hauteur $inf(f)$ sur [a, b]. De même, la somme supérieure est majorée par le rectangle de largeur (b−a) et de hauteur $sup(f)$ .

(b-a)\inf _{[a,b]}f\leq L_{f,P}\leq U_{f,P}\leq (b-a)\sup _{[a,b]}f

Les intégrales de Darboux inférieure et supérieure vérifient

${\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\leq {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x$
Relation de Chasles

Pour tout $c$ en $(a, b)$

${\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x={\underline {\int _{a}^{c}}}f(x)\,\mathrm {d} x+{\underline {\int _{c}^{b}}}f(x)\,\mathrm {d} x\quad ,\quad {\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x={\overline {\int _{a}^{c}}}f(x)\,\mathrm {d} x+{\overline {\int _{c}^{b}}}f(x)\,\mathrm {d} x$
Quasi-linéarité

Les intégrales de Darboux inférieure et supérieure ne sont pas nécessairement linéaires. Supposons $g :[a, b] \to R$ une fonction bornée, on a alors les inégalités :

{\begin{aligned}{\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x+{\underline {\int _{a}^{b}}}g(x)\,\mathrm {d} x&\leq {\underline {\int _{a}^{b}}}(f(x)+g(x))\mathrm {d} x\\[6pt]{\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x+{\overline {\int _{a}^{b}}}g(x)\,\mathrm {d} x&\geq {\overline {\int _{a}^{b}}}(f(x)+g(x))\,\mathrm {d} x\end{aligned}}

Cependant, on a bien, pour tout $c \geq 0$ constant

{\begin{aligned}{\underline {\int _{a}^{b}}}cf(x)&=c{\underline {\int _{a}^{b}}}f(x)\\[6pt]{\overline {\int _{a}^{b}}}cf(x)&=c{\overline {\int _{a}^{b}}}f(x)\end{aligned}}

Cependant, si on a $c \leq 0$ , alors

{\underline {\int _{a}^{b}}}cf(x)\,\mathrm {d} x=c{\overline {\int _{a}^{b}}}f(x)\,\mathrm {d} x\quad ,\quad {\overline {\int _{a}^{b}}}cf(x)=c{\underline {\int _{a}^{b}}}f(x)\,\mathrm {d} x

On considère la fonction :

{\begin{aligned}&{}F:[a,b]\to \mathbb {R} \\&{}x\rightarrow {\underline {\int _{a}^{x}}}f(t)\,\mathrm {d} t\end{aligned}}

alors $F$ est Lipschitz-continue. Un résultat identique est vérifié pour $F$ définie à partir de l'intégrale de Darboux supérieure.

Exemples

Une fonction Darboux-intégrable

La fonction $f (x) = x$ est Darboux-intégrable sur tout intervalle $[a, b]$ .

On considère la partition P_n de $[a, b]$ en n sous-intervalles de même longueur (b-a)/n.

Comme $f$ est strictement croissante, les infimum sur tout sous-intervalle sont atteints en $a +(b-a)(k -1)/ n$ , et les supremum y sont atteints en $a +(b-a) k / n$ . Ainsi

{\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f\left(a+(b-a){\frac {k-1}{n}}\right){\frac {b-a}{n}}\\&=\sum _{k=1}^{n}\left(a+(b-a){\frac {k-1}{n}}\right){\frac {b-a}{n}}\\&=n\times a{\frac {b-a}{n}}+{\frac {(b-a)^{2}}{n^{2}}}\sum _{k=1}^{n}(k-1)\\&=a(b-a)+{\frac {(b-a)^{2}}{n^{2}}}\times {\frac {(n-1)n}{2}}\end{aligned}}

et

{\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f\left(a+(b-a){\frac {k}{n}}\right){\frac {b-a}{n}}\\&=a(b-a)+{\frac {(b-a)^{2}}{n^{2}}}\times {\frac {n(n+1)}{2}}\end{aligned}}

On a alors

U_{f,P_{n}}-L_{f,P_{n}}={\frac {(b-a)^{2}}{n}}

Alors pour tout ε > 0, en choisissant une partition $P n$ avec $n>{\frac {(b-a)^{2}}{\epsilon }}$ satisfait

U_{f,P_{n}}-L_{f,P_{n}}<\epsilon

ce qui prouve que $f$ est Darboux-intégrable. La valeur de l'intégrale est alors

\int _{a}^{a}f(x)\,\mathrm {d} x=\lim _{n\to \infty }U_{f,P_{n}}=\lim _{n\to \infty }L_{f,P_{n}}={\frac {b^{2}-a^{2}}{2}}

Sommes de Darboux

Sommes de Darboux supérieures pour la fonction

y = x 2

Sommes de Darboux inférieures pour la fonction

y = x 2

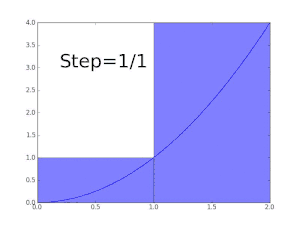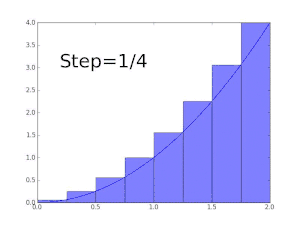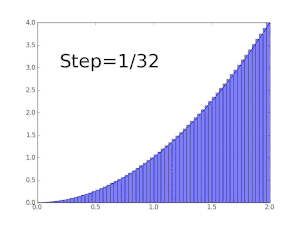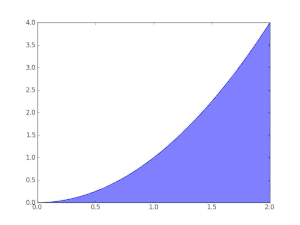
Une fonction non intégrable

On considère la fonction indicatrice des rationnels sur [0 ; 1] :

{\begin{aligned}\chi _{\mathbb {Q} }:[0,1]&\mapsto \mathbb {R} \\x&\rightarrow {\begin{cases}0&{\text{si }}x\in \mathbb {Q} \\1&{\text{si }}x\notin \mathbb {Q} \end{cases}}\end{aligned}}

Comme les ensembles des nombres rationnels et irrationnels sont tous deux denses de R, alors sur tout sous-intervalle de toute partition, la fonction prendra les valeurs 0 et 1. Donc pour toute partition P, on a

{\begin{aligned}L_{\chi _{\mathbb {Q} },P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}\chi _{\mathbb {Q} }=0\\U_{\chi _{\mathbb {Q} },P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}\chi _{\mathbb {Q} }=1\end{aligned}}

Les intégrales de Darboux inférieure et supérieure seront donc toujours différentes et la fonction n'est pas Darboux-intégrable.

Raffinement d'une partition et relation à l'intégration de Riemann

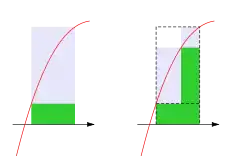
En passant à un raffinement, la somme inférieure augmente et la somme supérieure décroit.

Un raffinement de la partition $x 0, ..., x n$ est une autre partition $y 0, ..., y m$ telle que pour tout $i = 0, \dots, n$ il existe un entier $r (i)$ tel que

x_{i}=y_{r(i)}.

Un raffinement revient donc à découper les sous-intervalles en plus petits intervalles sans effacer les premiers pas. Alors, si $P' = (y 0, ..., y m)$ est un raffinement de $P = (x 0, ..., x n)$ , alors

U_{f,P}\geq U_{f,P'}

et

L_{f,P}\leq L_{f,P'}.

Si P₁, P₂ sont deux partitions du même intervalle (sans nécessairement que l'une soit un raffinement de l'autre), alors

L_{f,P_{1}}\leq U_{f,P_{2}},

et donc

L_{f}\leq U_{f}.

Sur une partition donnée, les sommes de Riemann seront comprises entre les sommes de Darboux inférieure et supérieure correspondantes. Formellement, si $P = (x 0, ..., x n)$ et $T = (t 0, ..., t n)$ forment ensemble une partition marquée :

x_{0}\leq t_{1}\leq x_{1}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}

(comme dans la définition de l'intégrale de Riemann), et si la somme de Riemann de $f$ correspondant à $P$ et $T$ est $R$ , alors

L_{f,P}\leq R\leq U_{f,P}.

De cette proposition, on tire que les intégrales de Riemann sont au moins aussi fortes que les intégrales de Darboux : si l'intégrale de Darboux existe, alors les sommes de Darboux inférieure et supérieure correspondant à une partition suffisamment fine sera proche de la valeur de l'intégrale, donc toute somme de Riemann sur la même partition sera également proche de la valeur de l'intégrale. Il y a ^{[réf. nécessaire]} une partition marquée qui sera arbitrairement proche de l'intégrale de Darboux inférieure ou supérieure, et par conséquent, si l'intégrale de Riemann existe, l'intégrale de Darboux doit aussi exister.

Voir aussi

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Darboux integral » (voir la liste des auteurs).

David J. Foulis et Mustafa A. Munem, After Calculus: Analysis, Dellen Publishing Company, 1989 (ISBN 978-0-02-339130-9, lire en ligne), p. 396
M. Spivak, Calculus (3rd. edition), Houston, TX, Publish Or Perish, Inc., 1994, 253–255 p. (ISBN 0-914098-89-6, lire en ligne)
W. Rudin, Principles of Mathematical Analysis (3rd. edition), New York, McGraw-Hill, 1976, 120–122 p. (ISBN 007054235X, lire en ligne)
(en) Eric W. Weisstein, « Darboux Integral », sur MathWorld
Spivak 2008, chapter 13.

Références

(en) Eric W. Weisstein, « Darboux Integral », sur MathWorld
Darboux integral at Encyclopaedia of Mathematics
(en) « Intégrale de Darboux », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
Michael Spivak, Calculus, Publish or Perish, 2008 (ISBN 978-0914098911, lire en ligne)

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] David J. Foulis et Mustafa A. Munem, After Calculus: Analysis, Dellen Publishing Company, 1989 (ISBN 978-0-02-339130-9, lire en ligne), p. 396

[2] M. Spivak, Calculus (3rd. edition), Houston, TX, Publish Or Perish, Inc., 1994, 253–255 p. (ISBN 0-914098-89-6, lire en ligne)

[3] W. Rudin, Principles of Mathematical Analysis (3rd. edition), New York, McGraw-Hill, 1976, 120–122 p. (ISBN 007054235X, lire en ligne)

[4] (en) Eric W. Weisstein, « Darboux Integral », sur MathWorld

[5] Spivak 2008, chapter 13.