Sujet
Pour télécharger le sujet de cette épreuve, cliquer sur ce lien.
Corrigé des exercices 1, 2 et 5
Pour un corrigé de tous les exercices, cliquer sur ce lien.
Exercice 1
Voir Produit scalaire dans l'espace/Exercices/Exercices#Exercice 2.
Exercice 2
Question 1
Voir Intégration de Riemann/Intégrale et primitives#Intégration par parties.
- Comme toute démonstration où l'énoncé n'introduit pas explicitement les éléments à manipuler, il faut commencer par présenter les éléments de travail par Soient et …
- Avant d'intégrer une relation, il faut bien écrire qu'elle est valable sur tout l'intervalle sur lequel on va intégrer :
pour tout . - Bien sûr, ne pas oublier de conclure.
Question 2
a
On va intégrer par parties de deux façons.
On choisit d'abord de poser sur l'intervalle les fonctions et telles que :
- , de primitive (par exemple) ;
- , de dérivée .
Les fonctions et sont bien dérivables à dérivée continue sur l'intervalle . On peut donc appliquer la formule d'intégration par parties :
Dans cette démonstration, le point-clé est l’application de la formule d'intégration par parties. Il faut bien expliciter l'hypothèse-phare de ce théorème avant de dérouler les calculs, à savoir :
- Les fonctions et doivent être dérivables à dérivée continue sur l'intervalle d'intégration.
De même, en posant :
- , de primitive (par exemple) ;
- , de dérivée ,
on obtient :
b
donc et .
Exercice 5
Partie A : Étude de certaines propriétés de la courbe C
Question 1
Soient définies par
- et .
Alors (pour tout )
- et donc
Question 2
- est strictement croissante sur ;
- est strictement croissante sur ;
- La somme de deux fonctions strictement croissantes est strictement croissante.
Donc est strictement croissante sur .
.
Par conséquent, est strictement négative sur et strictement positive sur . Puisque est du même signe, on en déduit le tableaux de variations suivant pour :
Question 3
Soit .
L'unique point d'intersection de et est donc l'origine du repère : .
Partie B : Étude d'une suite récurrente définie à partir de la fonction f
Question 1
est croissante sur donc
- .
Question 2
a
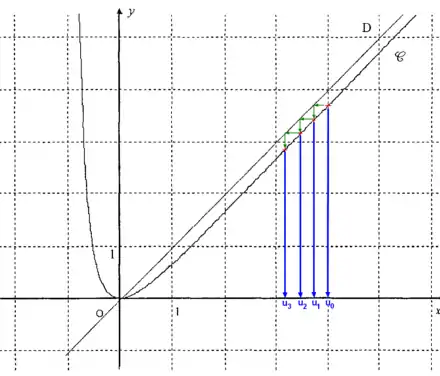
b
Montrons par récurrence que pour tout , .
- Initialisation : .
- Hérédité : soit tel que . Alors, d'après la question B.1, .
Le principe de récurrence permet de conclure.
c
Pour tout , car .
La suite est donc décroissante.
d
Puisque est décroissante et minorée (par ), elle converge.
e
Puisque la suite est récurrente de la forme avec continue,
sa limite est un réel tel que ,
c'est-à-dire (d'après la question A.3) : .