On rappelle que si et sont des fonctions numériques continues sur un intervalle fermé borné , avec , telles que , pour tout de , alors :
- .
On note l'ensemble des nombres réels et l'ensemble des nombres réels positifs.
1° On considère la fonction de dans définie par . Démontrer que c'est une bijection de sur .
- Dans toute la suite du problème, on désignera par la fonction réciproque de cette bijection. Préciser le domaine de définition de , ainsi que les nombres , , et .
- Tracer dans un repère orthonormal la courbe représentative de la fonction de dans définie par ; en déduire sur le même graphique la courbe représentative de la fonction .
2° En admettant que est dérivable (voir Fonctions circulaires réciproques/Fonction arctan, niveau 14), retrouver que pour tout réel .
- Calculer et en déduire la valeur de .
- Démontrer alors que la fonction qui, à tout réel , associe si et si , est continue en .
- Démontrer ensuite qu'elle est continue sur tout .
3° En étudiant les variations sur des deux fonctions et , démontrer que :
- , pour tout .
Dans toute la suite du problème, on considère la fonction , de dans , définie par :
(On ne cherchera pas à calculer l'intégrale qui définit .)
1° Démontrer que :
- , si .
2° En utilisant Ⅰ - 3° et Ⅱ - 1°, démontrer que (pour tout )
- .
- En déduire que est dérivable en (à droite) et que .
3° Démontrer que si :
- .
- En écrivant , en déduire que .
1° Vérifier que (pour tout )
- .
2° On pose , pour tout . Vérifier que :
- .
3° Étudier la variation de la fonction définie sur par . En déduire le signe de , puis de pour tout .
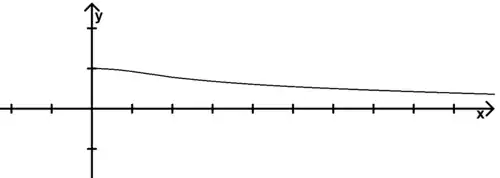
4° Rassembler les résultats des parties Ⅱ et Ⅲ pour donner l'allure de la courbe représentative de dans un repère orthonormal.
1° donc est continue et strictement croissante. et .
- est définie sur . , , , et .
- La courbe représentative de la fonction se déduit de la courbe représentative de la fonction tangente par symétrie par rapport à la droite d'équation y = x (première bissectrice) que nous avons appelée sur le tracé ci-dessous :

2° est la fonction réciproque de la fonction tan. Nous avons donc :
- Dérivons les deux membres de cette égalité, nous obtenons :
- qui se simplifie ainsi :
- D’où nous tirons :
- En particulier, ce qui prouve que la fonction qui à associe si et si est continue en .
- En tout autre réel, elle est continue comme quotient de deux fonctions continues dont la seconde ne s'annule pas.
3° La fonction a pour dérivée donc elle est strictement croissante. Puisqu'elle est nulle en , elle est strictement positive sur .
- La fonction a pour dérivée donc elle est strictement décroissante. Puisqu'elle est nulle en , elle est strictement négative sur .
- Les deux inégalités voulues en résultent.
1° Pour tout , .
2° Pour tout , est compris entre et .
- D'après le théorème des gendarmes, on a donc , c'est-à-dire .
3° Pour tout , est compris entre et , or .
- D'après le théorème des gendarmes, on a donc : .
- En ajoutant membre à membre , on obtient ainsi : .
1° Sur , la fonction est dérivable, de dérivée , donc est dérivable et
- ,
- c'est-à-dire :
- .
2° Par conséquent, pour tout ,
- ,
- c'est-à-dire (compte tenu de Ⅰ-2) :
- .
3° Pour tout , donc , ce qui montre que est strictement décroissante.
- Comme , donc donc est strictement décroissante aussi et (par le même raisonnement) également.
- La courbe a une tangente horizontale au point et a pour asymptote l'axe des abscisses.
- L'allure de la courbe représentative est alors :