Fonctions d'une variable réelle/Convexité

Définition et interprétation graphique

Définition

Une fonction $f:I\to \mathbb {R}$ définie sur un intervalle $I$ est dite convexe sur $I$ si :

$\forall x,y\in I\quad \forall t\in [0,1]\quad f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)$ .

Remarque

Pour que l'inégalité ci-dessus soit vraie pour tous $x,y\in I$ et tout $t\in [0,1]$ , il suffit qu'elle le soit lorsque $x<y$ et $t\in ]0,1[$ .

Illustration de la convexité.

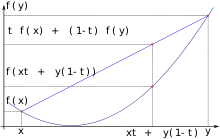
Interprétation graphique : Cela signifie que, si $A(x,f(x))$ et $B(y,f(y))$ sont deux points de la courbe représentative de $f$ , alors le segment $[AB]$ est au-dessus de l'arc ${\overset {{}_{\displaystyle \frown }}{AB}}$ de la courbe de $f$ .

Convexité et continuité

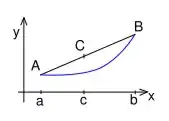
Illustration de l'inégalité des pentes.

Inégalité des pentes

Soit $f$ une fonction définie sur un intervalle $I$ . Si $f$ est convexe alors, pour tous $a<c<b$ dans $I$ :

${\frac {f(c)-f(a)}{c-a}}\leq {\frac {f(b)-f(a)}{b-a}}\leq {\frac {f(b)-f(c)}{b-c}}$

et par conséquent,

${\frac {f(c)-f(a)}{c-a}}\leq {\frac {f(b)-f(c)}{b-c}}$ .

Réciproquement, si l'une des trois inégalités est vérifiée pour tous $a<c<b$ dans $I$ alors $f$ est convexe.

Démonstration

Pour tous $a,b,c\in I$ tels que $a<c<b$ , chacune de ces trois inégalités se réécrit :

f(c)\leq {\frac {b-c}{b-a}}f(a)+{\frac {c-a}{b-a}}f(b)

.

Elles sont donc équivalentes.

Par ailleurs, pour tous $a,b,c,t\in \mathbb {R}$ tels que $a\neq b$ , on a :

$c=ta+(1-t)b\Leftrightarrow t={\frac {b-c}{b-a}}\Leftrightarrow 1-t={\frac {c-a}{b-a}}$ ;
$ta+(1-t)b$ est strictement compris entre $a$ et $b$ si et seulement si $t\in ]0,1[$ .

Par conséquent, l'une des trois inégalités est vérifiée pour tous $a,b,c\in I$ tels que $a<c<b$ si et seulement si, pour tous $a<b$ dans $I$ et tout $t\in ]0,1[$ , $f(ta+(1-t)b)\leq tf(a)+(1-t)f(b)$ , c'est-à-dire si $f$ est convexe.

L'inégalité des pentes est utilisée pour démontrer la propriété suivante, admise car de niveau supérieur à celui de ce chapitre.

Propriété

Toute fonction convexe sur un intervalle ouvert est continue.

Convexité et dérivabilité

On déduit finalement de cette étude les propriétés utilisées en pratique pour caractériser les fonctions convexes dérivables :

Propriété : Caractérisation des fonctions convexes dérivables

Une fonction $f$ dérivable sur un intervalle $I$ est convexe si et seulement si sa dérivée $f'$ est croissante sur $I$ .

Mais il y aussi son corollaire, qui est la propriété la plus utile en pratique :

Corollaire

Soit $f$ une fonction deux fois dérivable sur un intervalle $I$ .

$f''\geq 0\Rightarrow f\,{\mbox{convexe}}$ .

Cette propriété et ce corollaire sont démontrés dans la leçon spécialisée : Fonctions convexes.

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.