Fonction dérivée/Équation d'une tangente

Exemple

On a tracé la courbe représentative d'une fonction ƒ dont on ne précise pas la formule algébrique.

On donne :

$f(-2)=-{\frac {1}{4}}$ et $f'(-2)=-{\frac {3}{8}}$

Tracer la tangente à la courbe de ƒ au point $\left(-2,-{\frac {1}{4}}\right)$

Solution

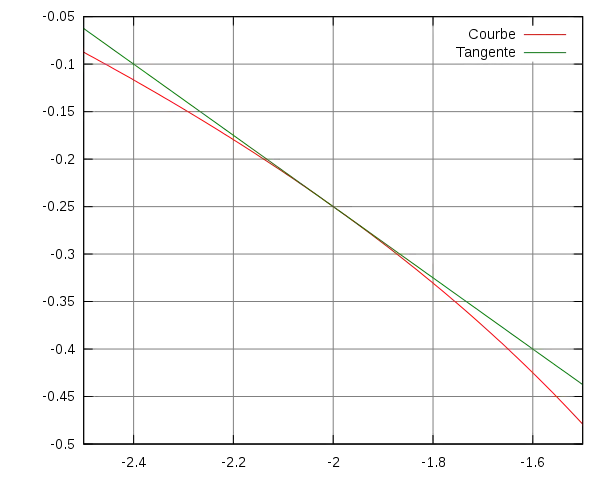
Calculer une équation de cette tangente en utilisant la formule donnant l'équation d'une droite connaissant un point et le coefficient directeur.

Solution

On pose $y=ax+b$ l'équation de la tangente à la courbe de ƒ au point d'abscisse -2.
On sait que le nombre dérivé de ƒ en -2 vaut $-{\frac {3}{8}}$ , donc $a=-{\frac {3}{8}}$
La droite passe par le point de coordonnées $\left(-2,-{\frac {1}{4}}\right)$ , donc $-{\frac {3}{8}}\times (-2)+b=-{\frac {1}{4}}$

On aboutit à

b=-1

.

Finalement, l'équation de la tangente à la courbe de ƒ au point d'abscisse -2 est $y=-{\frac {3}{8}}x-1$

Équation d'une tangente

On adapte la formule utilisée précédemment de façon à obtenir une formule donnant directement l'équation de la tangente à une courbe connaissant le nombre dérivé et la valeur de la fonction au point considéré.

Théorème

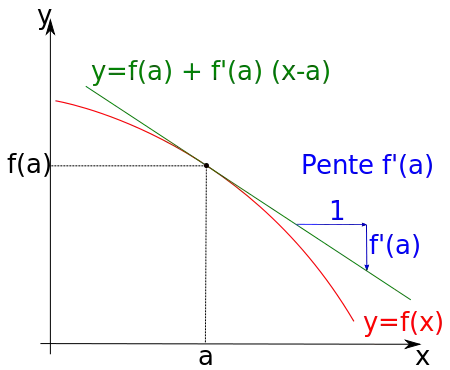
Si $f$ est dérivable en $a$ , alors

l'équation de la tangente à la courbe de $f$ au point $(a,f(a))$ est :

y=f'(a)(x-a)+f(a)

.

Démonstration

La tangente est la droite passant par le point $(a,f(a))$ et de coefficient directeur $f^{\prime }(a)$ .

Un autre point $(x,y)$ appartient à cette droite si et seulement si :

{\frac {y-f(a)}{x-a}}=f'(a)

,

c'est-à-dire

y-f(a)=f'(a)(x-a)

.

La tangente a donc bien pour équation

y=f'(a)(x-a)+f(a)

.

Complément : si $\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}=+\infty$ ou $-\infty$ alors $f$ n’est pas dérivable en $a$ , mais la courbe a encore une tangente au point $(a,f(a))$ : la droite verticale d'équation $x=a$ .

Approximation affine d'une fonction dérivable en un point

Voir les exercices sur : Approximation affine locale.

Pour $x$ voisin de $a$ , $f(x)$ est proche de la fonction affine $g(x)=f(a)+f'(a)(x-a)$ (la courbe est très proche de sa tangente).

Définition

Une approximation affine de $f$ au voisinage de $a$ est donnée par : $f(x)\approx f(a)+f'(a)(x-a)$ .

Cette approximation ne peut être faite qu'au voisinage du point d'abscisse

a

car elle traduit le fait que, au voisinage de

a

, la courbe de ƒ peut être assimilée à sa tangente avec peu d'erreur.

Cette propriété est utile pour les méthodes de résolution numérique d'équations différentielles comme la méthode d'Euler.

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.