Calcul avec les nombres complexes/Module et argument

Module d’un nombre complexe

Définition

Le module d’un nombre complexe $\left|z\right|$ est la distance qui sépare l'origine du repère complexe au point M d'affixe z.
De plus, pour $z=x+iy$ , on a :

$\left|z\right|={\sqrt {{x}^{2}+{y}^{2}}}={\sqrt {z{\bar {z}}}}$

Démonstration

Démonstration

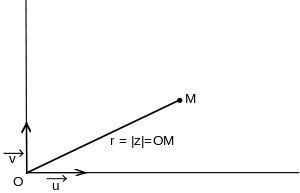
L'égalité $|z|={\sqrt {{x}^{2}+{y}^{2}}}$ découle du théorème de Pythagore.

De plus :
$z\times {\bar {z}}=(x+iy)(x-iy)={x}^{2}+{y}^{2}$ , d'où $\left|z\right|={\sqrt {z{\bar {z}}}}$

Distance entre deux points

Théorème

La distance entre A et B, respectivement d'affixes $z_{A}$ et $z_{B}$ , est donnée par : $AB=\|{\overrightarrow {AB}}\|=\left|z_{B}-z_{A}\right|={\sqrt {{(x_{B}-x_{A})}^{2}+{(y_{B}-y_{A})}^{2}}}$

Démonstration

Démonstration

Soient deux points A et B respectivement d'affixe $z_{A}=x_{A}+iy_{A}$ et $z_{B}=x_{B}+iy_{B}$ on a :
$AB=\|{\overrightarrow {AB}}\|=\left|z_{B}-z_{A}\right|$
Or $z_{B}-z_{A}=(x_{B}-x_{A})+i(y_{B}-y_{A})$
D'où $AB={\sqrt {{(x_{B}-x_{A})}^{2}+{(y_{B}-y_{A})}^{2}}}$

Exemples d’utilisation du module : Distance de deux points

Calculer la distance $AB$ où $z_{A}=5-i$ et $z_{B}=3+4i$ sont les affixes des deux points.
$AB=\left|z_{B}-z_{A}\right|=\left|(3+4i)-(5-i)\right|=\left|-2+5i\right|={\sqrt {{(-2)}^{2}+{5}^{2}}}={\sqrt {4+25}}={\sqrt {29}}$
La distance AB est donc ${\sqrt {29}}$

Argument d’un nombre complexe non nul

Définition

Soit $z=x+iy$ un nombre complexe non nul.

Une mesure en radians $\theta$ de l'angle $({\vec {u}},{\overrightarrow {OM}})$ est appelé argument de z.
On le note souvent $arg(z)$ .
L'argument est défini à $2\pi$ près.
On appelle argument principal celui qui est compris dans ${\displaystyle ]-\pi$ .

Exemple

Soit z = 32 + 12 i . Trouver 3 arguments de z, donner l'argument principal.

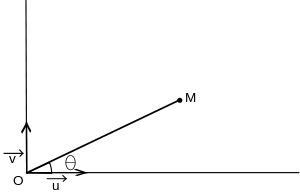
Écriture trigonométrique

Cosinus et sinus

Soit $z=x+iy$ un nombre complexe non nul, son module $|z|$ , d'argument principal $\theta$ , et M le point d'affixe z.

On considère le triangle dans le plan complexe, formé par l'origine, M et son projeté orthogonal sur l’axe des réels.

Les calculs respectivement du cosinus et du sinus d’une mesure de l'angle orienté $({\vec {u}},{\overrightarrow {OM}})$ donnent les deux propriétés suivantes :

Propriétés

$\cos(\theta )={\frac {x}{|z|}}$ : le cosinus de l'angle est le quotient de la partie réelle et du module.
$\sin(\theta )={\frac {y}{|z|}}$ : le sinus de l'angle est le quotient de la partie imaginaire et du module.

Forme trigonométrique

On sait que : $\cos(\theta )={\frac {x}{|z|}}\Leftrightarrow x=|z|\cos(\theta )$ et $\sin(\theta )={\frac {y}{|z|}}\Leftrightarrow y=|z|\sin(\theta )$ .

Et on a alors : $z=x+iy=|z|\cos(\theta )+i|z|\sin(\theta )=|z|(\cos(\theta )+i\sin(\theta ))$ .

Définition

On appelle la forme trigonométrique d’un nombre complexe z, l'écriture : $z=|z|(\cos(\theta )+i\sin(\theta ))$ de ce nombre pour n’importe quelle mesure de l'angle $\theta$ .

Dans cette écriture on retrouve directement le module et un argument (la plupart du temps l'argument principal).

Remarque importante : la forme trigonométrique d’un complexe est liée à ses coordonnées polaires $[r,\theta ]$ , tandis que la forme algébrique est liée à ses coordonnées cartésiennes $(x,y)$ .

Remarque : on note souvent $r$ pour le module de z, la forme trigonométrique se note donc aussi $z=r(\cos(\theta )+i\sin(\theta ))$ .

Changer d'écriture

Soit z un nombre complexe non nul, sous la forme $z=x+iy$ , de module $|z|$ et d'argument principal $\theta$ .

Les propriétés énoncées lors des calculs du cosinus et du sinus permettent de passer d’une écriture à une autre :

Passer d’une écriture trigonométrique à une écriture algébrique et vice-versa

${\begin{cases}\cos(\theta )=x~/~|z|\\\sin(\theta )=y~/~|z|\end{cases}}\Leftrightarrow {\begin{cases}x=|z|\cos(\theta )\\y=|z|\sin(\theta )\end{cases}}$ avec $|z|={\sqrt {x^{2}+y^{2}}}$ .

Exemple

La forme trigonométrique de $z=1-i$ est :

$z={\sqrt {2}}\left(\cos \left(-{\frac {\pi }{4}}\right)+i\sin \left(-{\frac {\pi }{4}}\right)\right)$ .

Il s'agit donc de trouver un facteur commun à x et y, ici ${\sqrt {2}}$ , puis d’identifier un angle connu.

Égalité de deux nombres complexes

Soient z et z' deux nombres complexes non nuls.

$z=z'\Leftrightarrow {\begin{cases}|z|=|z'|\\arg(z)=arg(z')[2\pi ]\end{cases}}$

Propriétés du module

Propriété

Les propriétés du module sont les mêmes que celles des normes vectorielles.

Opérations sur les modules :
- $\left|z_{1}\times z_{2}\right|=\left|z_{1}\right|\times \left|z_{2}\right|$
- $\left|{\frac {z_{1}}{z_{2}}}\right|={\frac {\left|z_{1}\right|}{\left|z_{2}\right|}}$
- $\left|z_{1}+z_{2}\right|\leq \left|z_{1}\right|+\left|z_{2}\right|$ (plus connue sous le nom d'inégalité triangulaire)

Module de l'opposé, du conjugué :
- $\left|-z\right|=\left|z\right|$
- $\left|{\bar {z}}\right|=\left|z\right|$

Propriétés algébriques de l'argument

Produit

Produit de deux nombres complexes

L'argument du produit de deux nombres complexes est la somme de leurs arguments : $arg(zz')=arg(z)+arg(z')[2\pi ]$ .

Démonstrations

Une démonstration géométrique

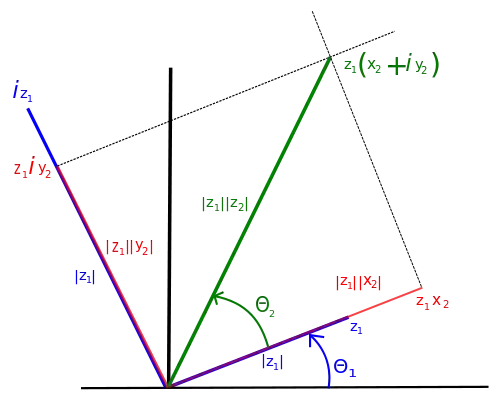
Considérons un nombre complexe $z_{1}$ , alors $z=r(\cos(\theta )+i\sin(\theta ))$ .

$z\times 1=z$ donc l'effet de la multiplication par $z_{1}$ sur le premier vecteur de base ${\overrightarrow {u}}$ est une rotation d'angle $\theta$ .
$z_{1}\times i=r(-\sin(\theta )+i\cos(\theta ))=r\left(\cos(\theta +{\frac {\pi }{2}})+i\sin(\theta +{\frac {\pi }{2}})\right)$

donc l'effet de la multiplication par

z_{1}

sur le second vecteur de base

{\overrightarrow {v}}

est également une rotation d'angle

\theta

Soit vecteur quelconque ${\overrightarrow {OM}}=a{\overrightarrow {u}}+b{\overrightarrow {v}}$ .

La multiplication par

z_{1}

étant distributive, son effet sur le vecteur

{\overrightarrow {OM}}

est encore une rotation d'angle

\theta

.

Soit un nombre complexe $z_{2}=a+i.b$ avec $arg(z_{2})=\theta _{2}$

alors $arg(z_{1}\times z_{2})$ est donc $\theta _{1}+\theta _{2}$

Démonstration (avec la forme trigonométrique)

Soit $z_{1}=\rho _{1}\times (\cos {(\theta _{1})}+i\sin {(\theta _{1})})$ et $z_{2}=\rho _{2}\times (\cos {(\theta _{2})}+i\sin {(\theta _{2})})$ avec $(\rho _{1},\rho _{2})\in {\mathbb {R} }^{2},(\theta _{1},\theta _{2})\in {[0;\pi ]}^{2},$ on prend $(k_{1},k_{2})=0$ pour simplifier les calculs.
${\begin{matrix}z_{3}&=&z_{1}\times z_{2}&=&\rho _{1}\times (\cos {(\theta _{1})}+i\sin {(\theta _{1})})\times \rho _{2}\times (\cos {(\theta _{2})}+i\sin {(\theta _{2})})\\&&&=&\rho _{1}\rho _{2}\times [(\cos {(\theta _{1})}\cos {(\theta _{2})}-\sin {(\theta _{1})}\sin {(\theta _{2})})+i(\sin {(\theta _{1})}\cos {(\theta _{2})}+\cos {(\theta _{1})}\sin {(\theta _{2})})]\\&&&=&\rho _{1}\rho _{2}\times [\cos {(\theta _{1}+\theta _{2})}+i\sin {(\theta _{1}+\theta _{2})}]\\&=&\rho _{3}[\cos {(\theta _{3})}+i\sin {(\theta _{3})}]\end{matrix}}$
Nous passons de la deuxième à la troisième ligne en utilisant les formules de trigonométrie ce qui nous donne:

$\cos {(a+b)}=\cos {a}\times \cos {b}-\sin {a}\times \sin {b}$
$\sin {(a+b)}=\sin {a}\times \cos {b}+\cos {a}\times \sin {b}$

On a donc $z_{3}=\rho _{3}[\cos {(\theta _{3})}+i\sin {(\theta _{3})}]$ et nous pouvons faire la même remarque.

Opposé d’un nombre complexe

L'argument de l'opposé d’un nombre complexe est : $arg(-z)=\pi +arg(z)[2\pi ]$ .

Inverse et division

Inverse d’un nombre complexe

L'argument de l'inverse d’un nombre complexe non nul est l'opposé de son argument : $arg\left({\frac {1}{z}}\right)=-arg(z)[2\pi ]$ .

Division de deux nombres complexes

D'après les règles de la multiplication et de l'inverse, on a, avec deux nombres complexes z et z' : $arg\left({\frac {z}{z'}}\right)=arg(z)-arg(z')[2\pi ]$ pour $z'\neq 0$ .

Puissance

Puissance d’un nombre complexe

Par extension à la multiplication et à l'inverse, on a l'argument d’un nombre complexe puissance n, qui est n fois son argument : $arg({z}^{n})=n\times arg(z)[2\pi ]$ avec $n\in \mathbb {Z}$ .

Conjugués

Conjugué d’un nombre complexe

L'argument du conjugué d’un nombre complexe est l'opposé de son l'argument : $arg({\bar {z}})=-arg(z)[2\pi ]$ .

Cela s'explique par le fait que le conjugué d’un nombre complexe est le symétrique par rapport à l’axe des réels du nombre complexe en question.

Produit d’un nombre complexe et de son conjugué

L'argument du produit d’un nombre complexe et de son conjugué est : $arg(z{\bar {z}})=arg(z)+arg({\bar {z}})=arg(z)-arg(z)=0[2\pi ]$ .

C'est une explication géométrique de pourquoi le produit d’un nombre complexe et de son conjugué est un réel positif.

Calcul de l'argument

Calcul avec le cosinus et le sinus

Connaissant la partie réelle et imaginaire d’un nombre complexe, on peut calculer son $\cos(\theta )$ et son $\sin(\theta )$ .

Propriétés

Soit $z=x+iy$ un nombre complexe non nul et $\theta$ l'argument principal que l’on cherche à connaître.

$\cos(\theta )={\frac {x}{|z|}}={\frac {x}{\sqrt {x^{2}+y^{2}}}}$
$\sin(\theta )={\frac {y}{|z|}}={\frac {y}{\sqrt {x^{2}+y^{2}}}}$

Il faut ensuite en déduire un angle $\theta$ en « reconnaissant » les valeurs usuelles de cosinus et sinus.

Exemple

Si $z=1-i$ alors $r={\sqrt {2}}$ .
Donc :
$\cos(\theta )={\frac {x}{r}}={\frac {\sqrt {2}}{2}}$ et $\sin(\theta )={\frac {y}{r}}=-{\frac {\sqrt {2}}{2}}$
On reconnait alors : $\theta =-{\frac {\pi }{4}}$ .

Propriété

Si on ne reconnaît aucun angle particulier, on peut utiliser les fonctions trigonométriques réciproques :

$\theta =\arccos \left({\frac {x}{|z|}}\right)=\arcsin \left({\frac {y}{|z|}}\right)$

Calcul avec la tangente

Propriété

Soit $z=x+iy$ .

On a si et seulement si z n’est pas un imaginaire pur, c'est-à-dire $x\neq 0$ :
$\tan(\theta )={\frac {y}{x}}$
Ce qui implique que :
$\theta \equiv \arctan \left({\frac {y}{x}}\right)\mod \pi$

L'argument est alors déterminé à $\pi$ près, il faut décider entre $\theta$ et $\theta +\pi$ en utilisant le signe de $x$ (généralement, on cherche la mesure principale, c’est celle qui est dans ]- ${\displaystyle \pi$ ] ):

si $x>0$ alors $\theta$ est dans $\left]-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]$
si $x=0$ alors si $y>0$ alors $\theta ={\frac {\pi }{2}}$ et si $y<0$ alors $\theta =-{\frac {\pi }{2}}$

si $x<0$ alors $\theta$ est dans ${\displaystyle \left]-\pi$

Remarque : Une rapide représentation des complexes $1$ , $-1$ , $i$ et $-i$ sur le cercle trigonométrique permet de synthétiser les règles précédentes.
Remarque : Les calculatrices renvoient généralement l'angle dans $\left]-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]$ mais ce résultat doit être révisé suivant la règle ci-dessus. Notons qu'en électricité, l'argument est :

Inférieur ou égal à

\pi /2

pour les montages du premier ordre (RC ou RL).

Inférieur ou égal à

\pi

pour les montages du second ordre (RLC).

Inférieur ou égal à

3\pi /2

pour les montages du troisième ordre.

Inférieur ou égal à

2\pi

pour les montages du quatrième ordre. Il faut donc impérativement tenir compte des modifications des remarques précédentes, en particulier pour l'étude de la stabilité des systèmes bouclés (se référer aux cours d'automatique).
Remarque: En électronique la phase est fonction de la fréquence du signal qui parcourt le système.

Argument d’une différence

Propriété

Si A et B sont deux points distincts d'affixes respectives a et b.

alors

{\displaystyle arg(b-a)=({\vec {u}}\

Si A, B, C et D sont quatre points deux à deux distincts d'affixes respectives a, b, c et d :

alors :

$\arg \left({\frac {d-c}{b-a}}\right)=({\overrightarrow {AB}},{\overrightarrow {CD}})$

Voir les exercices sur : Calcul de modules et d'arguments.

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.