Topologie initiale
En mathématiques, plus précisément en topologie, la topologie initiale, sur un ensemble muni d'une famille d'applications à valeurs dans des espaces topologiques, est la topologie la moins fine pour laquelle toutes ces applications sont continues. Deux cas particuliers importants de topologies initiales sont la topologie induite et la topologie produit. La notion duale est celle de topologie finale.
Définition
Soient X un ensemble et (fi)i∈I une famille d'applications, chacune définie sur X et à valeurs dans un espace topologique Yi. La topologie initiale associée à ces données est la moins fine topologie sur X pour laquelle toutes les fi sont continues.
Autrement dit, c'est la topologie engendrée par l'ensemble de toutes les parties de X de la forme fi−1(U), où i appartient à I et où U est un ouvert de l'espace Yi correspondant.
Exemples
- Sur une partie d'un espace topologique, la topologie induite est la topologie initiale associée à l'injection canonique.
- Sur un ensemble-produit d'(ensembles sous-jacents à des) espaces topologiques, la topologie produit est la topologie initiale associée aux projections canoniques.
- Une limite projective d'espaces topologiques est la limite projective des ensembles sous-jacents (qui est une partie du produit) munie, à nouveau, de la topologie initiale associée aux projections.
- La topologie faible sur un espace vectoriel topologique est la topologie initiale associée aux éléments de son dual topologique, c'est-à-dire aux formes linéaires continues.
- Dans le treillis des topologies sur un ensemble X, la borne supérieure d'une famille (τi)i∈I, c'est-à-dire la topologie engendrée par l'union des topologies τi (vues comme ensembles d'ouverts), est la topologie initiale associée aux fonctions idX : X → (X, τi).
- Une topologie est complètement régulière si et seulement si elle est initiale pour la famille de ses fonctions continues (ou celle de ses fonctions continues bornées) à valeurs dans ℝ.
- Toute topologie est initiale pour la famille de ses fonctions continues à valeurs dans l'espace de Sierpiński.
Propriétés
Caractérisation
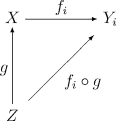
Cette topologie initiale sur X est caractérisée par la propriété universelle suivante : pour tout espace topologique Z, une application g : Z → X est continue (X étant muni de la topologie initiale) si — et bien sûr seulement si — toutes les applications fi∘g : Z → Yi le sont.
Cela résulte immédiatement de la définition de la topologie initiale par une prébase et du critère de continuité associé.
Plongement dans le produit
La topologie initiale sur X est la moins fine pour laquelle l'application canonique f, de X dans le produit des Yi, est continue. Cette application f est alors un plongement si (et seulement si) elle est injective, autrement dit si la famille des fi est séparante (en), c'est-à-dire si pour tous points distincts x et y dans X, il existe un indice i tel que fi(x) ≠ fi(y).
Famille séparant les points des fermés
Pour qu'une topologie donnée sur X coïncide avec la topologie initiale associée aux fi, une condition suffisante est que les fi−1(U), pour i ∈ I et U ouvert de Yi, en forment non seulement une prébase mais une base. On démontre que cette condition équivaut à ce que la famille des fi sépare les points des fermés, c'est-à-dire que pour tout fermé F de X et tout point x de X n'appartenant pas à F, il existe un indice i tel que fi(x) ne soit pas adhérent à fi(F).
Si de plus X est un espace T0, les fi séparent aussi les points donc X est plongé dans le produit des Yi.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Initial topology » (voir la liste des auteurs).
- N. Bourbaki, Éléments de mathématique, livre III : Topologie générale [détail des éditions], chapitres 1 à 4
- (en) Stephen Willard, General Topology, Dover, (1re éd. 1970, Addison-Wesley), 384 p. (ISBN 978-0-486-13178-8, lire en ligne)
Articles connexes
- Portail des mathématiques