Porte quantique

En informatique quantique, et plus précisément dans le modèle de circuit quantique (en) de calcul, une porte quantique (ou porte logique quantique) est un circuit quantique élémentaire opérant sur un petit nombre de qubits. Les portes quantiques sont les briques de base des circuits quantiques, comme le sont les portes logiques classiques pour des circuits numériques classiques.

Contrairement à de nombreuses portes logiques classiques, les portes logiques quantique sont « réversibles ». Cependant, il est possible d'effectuer un calcul classique en utilisant uniquement des portes réversibles. Par exemple, la porte de Toffoli réversible peut implémenter toutes les fonctions Booléennes, souvent au prix de devoir utiliser des bits auxiliaires (en). La porte de Toffoli a un équivalent quantique direct, montrant que des circuits quantiques peuvent effectuer toutes les opérations effectuées par les circuits classiques.

Les portes logiques quantiques sont représentées par des matrices unitaires. Les portes quantiques les plus courantes fonctionnent sur des espaces d'un ou deux qubits, tout comme les portes logiques classiques fonctionnent sur un ou deux bits. Les portes quantiques peuvent être décrites comme des matrices unitaires de taille $2^{n}\times 2^{n}$ , où $n$ est le nombre de qubits sur lesquels la porte agit. Les variables sur lesquelles les portes agissent, les états quantiques, sont des vecteurs dans $2^{n}$ dimensions complexes, où $n$ est, à nouveau, le nombre de qubits de la variable: Les vecteurs de base sont les résultats possibles de la mesure, si elle est effectuée, et un état quantique est une combinaison linéaire de ces résultats.

Représentation matricielle

Les portes quantiques sont généralement représentées par des matrices. Une porte qui agit sur k qubits est représentée par une matrice unitaire $2^{k}\times 2^{k}$ . Les nombres de qubits en entrée et en sortie de la porte doivent être égaux. L'action de la porte sur un état quantique spécifique est obtenu en multipliant le vecteur qui représente l'état par la matrice qui représente la porte.

La représentation vectorielle d'un qubit unique est

v_{0}|0\rangle +v_{1}|1\rangle \rightarrow {\begin{bmatrix}v_{0}\\v_{1}\end{bmatrix}}

,

et la représentation vectorielle de deux qubits est

v_{00}|00\rangle +v_{01}|01\rangle +v_{10}|10\rangle +v_{11}|11\rangle \rightarrow {\begin{bmatrix}v_{00}\\v_{01}\\v_{10}\\v_{11}\end{bmatrix}}

,

où $|ab\rangle$ est à la base du vecteur représentant un état où le premier qubit est dans l'état $|a\rangle$ et le second qubit dans l'état $|b\rangle$ .

Portes couramment utilisées

Porte de Hadamard (H)

La porte de Hadamard agit sur un seul qubit. Elle transforme l'état basique $|0\rangle$ en ${\frac {|0\rangle +|1\rangle }{\sqrt {2}}}$ et l'état $|1\rangle$ en ${\frac {|0\rangle -|1\rangle }{\sqrt {2}}}$ , ce qui signifie que la mesure aura la même probabilité de donner 1 ou 0 (c'est-à-dire crée une superposition). Elle représente une rotation de $\pi$ sur l'axe $({\hat {x}}+{\hat {z}})/{\sqrt {2}}$ . De manière équivalente, c'est la combinaison de deux rotations, $\pi$ sur l'axe des X, suivie par $\pi /2$ sur l'axe des ordonnées. Ce qui est représenté par la matrice de Hadamard:

Représentation de la porte de Hadamard

H={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}

.

La porte de Hadamard est une version qubit de la transformée de Fourier quantique (en).

Puisque $HH^{*}=I$ où I est la matrice identité, H est en effet une matrice unitaire (en).

Porte Pauli-X (= Porte NOT)

Schéma quantique de la porte NOT

La porte Pauli-X agit sur un seul qubit. Elle transforme $|0\rangle$ en $|1\rangle$ et $|1\rangle$ en $|0\rangle$ . C'est pourquoi elle est parfois appelée bit-flip.

C'est l'équivalent quantique de la porte NOT des ordinateurs classiques. Elle équivaut à une rotation de la sphère de Bloch autour de l'axe X par $\pi$ radians.

Elle est représentée par la matrice de Pauli X :

X={\begin{bmatrix}0&1\\1&0\end{bmatrix}}

Porte Pauli-Y

La porte Pauli-Y agit sur un seul qubit. Elle transforme $|0\rangle$ en $\mathrm {i} |1\rangle$ et $|1\rangle$ en $-\mathrm {i} |0\rangle$ .

Elle équivaut à une rotation autour de l'axe Y de la sphère de Bloch par $\pi$ radians.

Elle est représentée par la matrice de Pauli Y :

Y={\begin{bmatrix}0&-\mathrm {i} \\\mathrm {i} &0\end{bmatrix}}

Porte Pauli-Z ( $R_{\pi }$ )

La porte Pauli-Z agit sur un seul qubit. Elle laisse l'état de base $|0\rangle$ inchangé et transforme $|1\rangle$ en $-|1\rangle$ .

Elle équivaut à une rotation autour de l'axe Z de la sphère de Bloch par $\pi$ radians. C'est donc un cas particulier de la porte Changement de phase (voir ci-dessous) pour $\phi =\pi$ . De ce fait, elle est parfois appelée phase-flip.

Elle est représentée par la matrice de Pauli Z :

Z={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}

Porte Racine carrée de NON ( $\sqrtNON$ )

Schéma quantique de la racine carrée la porte NON

La porte Racine carrée de NON agit sur un seul qubit. Elle est représentée par cette matrice :

{\sqrt {NON}}={\frac {1}{2}}{\begin{bmatrix}1+\mathrm {i} &1-\mathrm {i} \\1-\mathrm {i} &1+\mathrm {i} \end{bmatrix}}

L'élévation au carré de cette matrice montre qu'il s'agit bien de la racine carrée d'une Porte NON :

${\sqrt {NON}}\,{\sqrt {NON}}={\frac {1}{2}}{\begin{bmatrix}1+\mathrm {i} &1-\mathrm {i} \\1-\mathrm {i} &1+\mathrm {i} \end{bmatrix}}.{\frac {1}{2}}{\begin{bmatrix}1+\mathrm {i} &1-\mathrm {i} \\1-\mathrm {i} &1+\mathrm {i} \end{bmatrix}}={\frac {1}{4}}{\begin{bmatrix}0&4\\4&0\end{bmatrix}}={\begin{bmatrix}0&1\\1&0\end{bmatrix}}=NON$

Note : Des portes racines-carrées peuvent être construites pour toutes les portes. Pour chacune d'elle, il s'agit de la matrice unitaire qui, multipliée par elle-même, donne cette porte. Toutes les fractions d'exposants (racines n-ièmes) de toutes les portes peuvent être créées selon le même principe (élévation à l'exposant n donnant la matrice d'origine de la porte de référence).

Les portes Changement de Phase ( $R_{\phi }$ ) ou (phase shift gates)

C'est une famille de portes qubit-unique qui laisse l'état basique $|0\rangle$ inchangé et transforme $|1\rangle$ en $e^{\mathrm {i} \phi }|1\rangle$ . Cette porte ne modifie pas la probabilité de mesurer un $|0\rangle$ ou $|1\rangle$ , mais elle modifie la phase de l'état quantique. Ceci équivaut à tracer un cercle horizontal à la latitude de $\phi$ radians sur la sphère de Bloch.

R_{\phi }={\begin{bmatrix}1&0\\0&e^{\mathrm {i} \phi }\end{bmatrix}}

où $\phi$ est le décalage de phase. Quelques exemples courants sont la porte T avec $\phi ={\frac {\pi }{4}}$ , la porte de phase avec $\phi ={\frac {\pi }{2}}$ et la porte Pauli-Z avec $\phi =\pi$ .

Porte Swap (S)

Représentation de la porte SWAP

La porte swap intervertit deux qubits. En respectant les bases $|00\rangle$ , $|01\rangle$ , $|10\rangle$ , $|11\rangle$ , elle est représentée par la matrice :

{\mbox{SWAP}}=S={\begin{bmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{bmatrix}}

.

Racine carrée de la porte Swap ( ${\sqrt {SWAP}}$ )

Representation de la porte

{\sqrt {\mbox{SWAP}}}

La porte ${\sqrt {SWAP}}$ effectue la moitié des chemins de deux qubits swap (interversion). Elle est universelle de sorte que n'importe quelle porte de qubits peut être construite à partir de cette seule porte et des portes à qubit unique.

{\sqrt {S}}={\sqrt {\mbox{SWAP}}}={\begin{bmatrix}1&0&0&0\\0&{\frac {1}{2}}(1+\mathrm {i} )&{\frac {1}{2}}(1-\mathrm {i} )&0\\0&{\frac {1}{2}}(1-\mathrm {i} )&{\frac {1}{2}}(1+\mathrm {i} )&0\\0&0&0&1\\\end{bmatrix}}

.

Les portes Contrôlée (cX cY cZ)

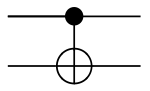
Représentation de la porte contrôlée NOT

Les portes contrôlée agissent sur 2 qubits ou plus, où un ou plusieurs qubits agissent comme un contrôle pour certaines opérations. Par exemple, la porte contrôlée NOT (ou CNOT ou cX) agit sur 2 qubits, et n'effectue l'opération NOT sur le second qubit que lorsque le premier qubit est $|1\rangle$ et sinon le laisse inchangé. Elles sont représentées par la matrice

{\mbox{CNOT}}=cX={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}}

.

Plus généralement, si U est une porte qui agit sur des qubits uniques en représentation matricielle

U={\begin{bmatrix}u_{00}&u_{01}\\u_{10}&u_{11}\end{bmatrix}}

,

alors la porte contrôlée-U est une porte qui fonctionne sur deux qubits de telle sorte que le premier qubit sert de contrôle. Il relie les états basiques comme suit.

Représentation de la porte contrôlée-U

|00\rangle \mapsto |00\rangle

|01\rangle \mapsto |01\rangle

|10\rangle \mapsto |1\rangle \otimes U|0\rangle =|1\rangle \otimes \left(u_{00}|0\rangle +u_{10}|1\rangle \right)

|11\rangle \mapsto |1\rangle \otimes U|1\rangle =|1\rangle \otimes \left(u_{01}|0\rangle +u_{11}|1\rangle \right)

{\mbox{C}}(U)={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&u_{00}&u_{01}\\0&0&u_{10}&u_{11}\end{bmatrix}}

.

controlled X-, Y- and Z- gates

controlled-X gate

controlled-Y gate

controlled-Z gate

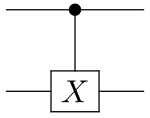
Lorsque U est l'une des matrices de Pauli, σ_x, σ_y, ou σ_z, les termes respectifs "contrôlée-X", "contrôlée-Y", ou "contrôlée-Z" sont parfois utilisés[1].

La porte CNOT est généralement utilisée dans l'informatique quantique pour générer des états intriqués.

Porte Toffoli (CCNOT)

Représentation de la porte de Toffoli

La porte de Toffoli, appelée aussi porte CCNOT ou porte Deutsch $D(\pi /2)$ , est une porte 3-bits, qui est universelle pour le calcul classique. La porte quantique de Toffoli est la même porte, définie pour 3 qubits. Si les deux premiers bits sont dans l'état $|1\rangle$ elle applique une Pauli-X (ou NOT) sur le troisième bit, sinon elle ne fait rien. C'est un exemple de porte contrôlée. Puisqu'elle est l'analogue quantique d'une porte classique, elle est complètement spécifiée par sa table de vérité.

Truth table

Matrix form

INPUT			OUTPUT
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	0	1
1	1	0	1	1	1
1	1	1	1	1	0

${\begin{bmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\\\end{bmatrix}}$

Elle peut également être décrite comme la porte qui relie $|a,b,c\rangle$ à $|a,b,c\oplus ab\rangle$ .

Porte Fredkin (CSWAP)

Article principal: la porte de Fredkin (en)

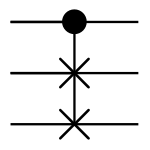
Représentation de la porte de Fredkin

La porte Fredkin (également CSWAP ou porte cS ) est une porte 3-bit qui effectue un échange contrôlé (controlled swap). Elle est universelle pour le calcul classique. Elle a la propriété utile de conserver les nombres de 0s et de 1s, ce qui dans le modèle de la boule de billard (en), signifie qu'il y a le même nombre de boules en sortie qu'en entrée.

Truth table

Matrix form

INPUT			OUTPUT
C	I₁	I₂	C	O₁	O₂
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	0	1
1	1	1	1	1	1

${\begin{bmatrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\\end{bmatrix}}$

Porte Ising (XX)

La porte d'Ising (ou porte XX) est une porte 2-bits qui est implémentée nativement dans certains ordinateurs quantiques à ions piégés[2]^,[3]. Elle est définie par

XX_{\phi }={\begin{bmatrix}\cos(\phi )&0&0&-\mathrm {i} \sin(\phi )\\0&\cos(\phi )&-\mathrm {i} \sin(\phi )&0\\0&-\mathrm {i} \sin(\phi )&\cos(\phi )&0\\-\mathrm {i} \sin(\phi )&0&0&\cos(\phi )\\\end{bmatrix}}

Porte Deutsch ( $D_{\theta }$ )

La porte Deutsch (ou $D_{\theta }$ ) est une porte à 3 qubits. Elle est définie par

|a,b,c\rangle \mapsto {\begin{cases}\mathrm {i} \cos(\theta )|a,b,c\rangle +\sin(\theta )|a,b,1-c\rangle &{\mbox{pour }}a=b=1\\|a,b,c\rangle &{\mbox{autrement.}}\end{cases}}

Portes Quantiques Universelles

CNOT et

{\sqrt {\mbox{SWAP}}}

sont des portes 2-qubits universelles et peuvent être transformées en l'une et l'autre.

De manière informelle, un ensemble de portes quantiques universelles est un ensemble de portes qui permet de représenter toute opération possible sur un ordinateur quantique c'est-à-dire que toute opération unitaire peut être exprimée comme une séquence finie de portes de cet ensemble. Théoriquement, c'est impossible car le nombre de portes quantiques est indénombrable, alors que le nombre de séquences finies d'un ensemble fini est dénombrable. Mais en pratique, nous avons seulement besoin que toute opération quantique puisse être approchée par une séquence de portes issues de cet ensemble fini. En outre, pour les transformations unitaires sur un nombre constant de qubits, le théorème de Solovay–Kitaev garantit que cela peut être fait de manière efficace.

Un ensemble simple de portes quantiques universelles à deux qubits est constitué de la porte de Hadamard $H$ , la porte $\pi /8$ $R_{Z}(\pi /4)=diag(1,e^{\frac {i\pi }{4}})$ et la porte contrôlée-NOT (CNOT) $cX$ [4].

Un ensemble de portes quantiques universelles à une seule porte peut également être formulé à l'aide de la porte Deutsch de trois-qubit $D(\theta )$ qui effectue la transformation[5]

|a,b,c\rangle \mapsto {\begin{cases}i\cos(\theta )|a,b,c\rangle +\sin(\theta )|a,b,1-c\rangle &{\mbox{pour }}a=b=1\\|a,b,c\rangle &{\mbox{sinon.}}\end{cases}}

La porte logique classique universelle, la porte de Toffoli, est réductible à la porte Deutsch, $D({\begin{matrix}{\frac {\pi }{2}}\end{matrix}})$ , montrant ainsi que toutes les opérations logiques classiques peuvent être effectuées sur un ordinateur quantique universel.

Un autre ensemble de portes quantiques universelles se compose de la porte d'Ising et de la porte Changement de phase (swap gate). Ce sont les ensembles de portes disponibles nativement dans certains ordinateurs quantiques à ions piégés .

Mesure

Représentation de la mesure. Les deux lignes sur le côté droit représentent un bit classique, la ligne seule sur le côté gauche représente un qubit.

La mesure semble similaire à une porte quantique, même si elle n'est pas une porte, parce que la mesure modifie activement la variable observée. La mesure prend un état quantique et le projette sur l'un des vecteurs de base, avec une probabilité égale au carré de la profondeur des vecteurs le long de ce vecteur de base. C'est une opération non-réversible, car elle définit l'état quantique égal au vecteur de base qui représente l'état mesuré (l'état est « réduit » à une valeur singulière définie). Le pourquoi et le comment sont l'objet du problème de la mesure.

Si deux registres quantique différents sont intriqués (ils ne sont pas linéairement indépendants), la mesure d'un registre affecte ou révèle l'état de l'autre registre en écrasant partiellement ou entièrement son état. Un exemple d'un tel état linéaire inséparable est la paire EPR, qui peut être construite avec les portes CNOT et Hadamard, décrites ci-dessus. Cet effet est utilisé dans de nombreux algorithmes: Si deux variables A et B sont intriquées au maximum (L'état de Bell en est l'exemple le plus simple), une fonction F est appliquée à A tel que A soit mis à jour à la valeur de F(A), suivie par la mesure de A, alors B sera mesurée à une valeur tel que F(B) = A. De cette façon, la mesure d'un registre peut être utilisée pour attribuer des propriétés à d'autres registres. Comme le démontrent les expériences sur les inégalités de Bell, ce type d'affectation se produit instantanément sur n'importe quelle distance.

Circuit de la composition et des états intriqués

Si deux qubits ou plus sont considérés comme un seul état quantique, cet état combiné est égal au produit tensoriel des qubits constitutifs (le produit de Kronecker en standard). Un état intriqué est un état qui ne peut pas être tenseur-factorisée (l'état ne peut pas être séparé en ses qubits constitutifs). Les portes CNOT, Ising et Toffoli sont des exemples de portes qui agissent sur les états construit de plusieurs qubits.

Le produit tensoriel de deux portes quantiques n-qubit génère la porte qui est égale à deux portes en parallèle. Cette porte va agir sur $2n$ qubits. Par exemple, la porte $G=H\otimes H$ est la porte de Hadamard ( $H$ ) appliquée en parallèle sur 2 qubits. Elle peut être écrite comme

$G=H\otimes H={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes {\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}={\frac {1}{2}}{\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix}}$

Cette porte "Hadamard parallèle à deux qubits", lorsqu'elle est appliquée, par exemple, au vecteur zéro à deux qubits $|00\rangle$ ,crée un état quantique qui a la même probabilité d'être observé dans l'un de ses quatre résultats possibles: 00, 01, 10 et 11. On peut écrire cette opération:

$G|00\rangle ={\frac {1}{2}}{\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\0\end{bmatrix}}={\frac {1}{2}}{\begin{bmatrix}1\\1\\1\\1\end{bmatrix}}={\frac {1}{2}}|00\rangle +{\frac {1}{2}}|01\rangle +{\frac {1}{2}}|10\rangle +{\frac {1}{2}}|11\rangle ={\frac {|00\rangle +|01\rangle +|10\rangle +|11\rangle }{2}}$

La probabilité d'observer tout état est la valeur absolue de l'amplitude au carré, ce qui dans l'exemple ci-dessus signifie qu'il y en a un sur quatre pour lequel nous observons l'une des quatre valeurs. (Les amplitudes sont des valeurs complexes, de sorte que leurs carrés ne sont pas toujours positifs.)

Si nous avons un ensemble de N qubits qui sont intriqués (leur état combiné ne peut pas être tenseur-factorisé en une expression de qubits individuels) et si nous souhaitons appliquer une porte quantique sur M < N qubits dans l'ensemble, nous devrons étendre la porte pour prendre N qubits. Cela peut être fait en combinant la porte avec une matrice d'identité , de sorte que leur produit tensoriel devienne une porte qui agit sur N qubits. La matrice identité ( $I$ ) est une représentation de la porte qui transformes chaque état en lui-même (c'est-à-dire, ne fait rien du tout). Dans un schéma de circuit, la porte d'identité ou la matrice apparaîtra comme un simple fil.

Par exemple, la transformée de Hadamard ( $H$ ) agit sur un seul qubit, mais si on nourrit, par exemple, le premier des deux qubits qui constituent l'état de Bell intriqué ${\frac {|00\rangle +|11\rangle }{\sqrt {2}}}$ , nous ne pouvons pas écrire cette opération facilement. Nous devons étendre la transformée de Hadamard avec la porte sans effet $I$ afin que nous puissions agir sur des états quantiques qui s'étendent sur deux qubits:

$M=H\otimes I={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes {\begin{bmatrix}1&0\\0&1\end{bmatrix}}={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&0&1&0\\0&1&0&1\\1&0&-1&0\\0&1&0&-1\end{bmatrix}}$

La porte $M$ peut maintenant être appliquée à n'importe quel état à deux bits, intriqués ou non. La porte M applique la transformation de Hadamard sur le 1er qubit et laisse le second intact. Si elle est appliquée à l'état de Bell, dans notre exemple, nous pouvons écrire que:

$M{\frac {|00\rangle +|11\rangle }{\sqrt {2}}}={\frac {1}{2}}{\begin{bmatrix}1&0&1&0\\0&1&0&1\\1&0&-1&0\\0&1&0&-1\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\1\end{bmatrix}}={\frac {1}{2}}{\begin{bmatrix}1\\1\\1\\-1\end{bmatrix}}={\frac {|00\rangle +|01\rangle +|10\rangle -|11\rangle }{2}}$

Parce que le nombre d'éléments dans les matrices est $2^{2x}$ où $x$ est le nombre de qubits sur lesquels les portes agissent, il est impossible de simuler les grands systèmes quantiques en utilisant des ordinateurs classiques.

On remarque par ailleurs que l'on peut faire le calcul en restant sous la notation de Dirac, par exemple :

$(H\otimes I)(|0\rangle \otimes |1\rangle )=H|0\rangle \otimes I|1\rangle ={\frac {|0\rangle +|1\rangle }{\sqrt {2}}}\otimes |1\rangle ={\frac {|01\rangle +|11\rangle }{\sqrt {2}}}$

L'histoire

La notation actuelle pour les portes quantiques a été développée par Barenco et coll.[6], en s'appuyant sur la notation introduite par Feynman[7].

Voir aussi

Les matrices de Pauli

Notes

M. Nielsen et I. Chuang, Calcul Quantique et l'Information Quantique, Cambridge University Press, 2000
http://online.kitp.ucsb.edu/online/mbl_c15/monroe/pdf/Monroe_MBL15Conf_KITP.pdf
http://iontrap.umd.edu/wp-content/uploads/2012/12/nature18648.pdf
M. Nielsen et I. Chuang, Calcul Quantique et l'Information Quantique, Cambridge University Press, 2016, p. 189; (ISBN 978-1-107-00217-3)
David Deutsch, « Quantum computational networks », Proc. R. Soc. Lond. A, vol. 425,‎ 1989, p. 73–90 (DOI 10.1098/rspa.1989.0099, Bibcode 1989RSPSA.425...73D)
Phys. Rév. Un 52 3457-3467 (1995), DOI:10.1103/PhysRevA.52.3457 10.1103; e-print « quant-ph/9503016 », texte en accès libre, sur arXiv.
R. P. Feynman, "mécanique Quantique" ordinateurs, de l'Optique News, février 1985, 11, p. 11; réimprimé dans les Fondations de la Physique 16(6) 507-531.

Références

M. Nielsen et I. Chuang, Calcul Quantique et l'Information Quantique, Cambridge University Press, 2000

Portail de l’informatique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] M. Nielsen et I. Chuang, Calcul Quantique et l'Information Quantique, Cambridge University Press, 2000

[2] ttp://online.kitp.ucsb.edu/online/mbl_c15/monroe/pdf/Monroe_MBL15Conf_KITP.pdf

[monroe2012-3] ttp://iontrap.umd.edu/wp-content/uploads/2012/12/nature18648.pdf

[4] M. Nielsen et I. Chuang, Calcul Quantique et l'Information Quantique, Cambridge University Press, 2016, p. 189; (ISBN 978-1-107-00217-3)

[5] David Deutsch, « Quantum computational networks », Proc. R. Soc. Lond. A, vol. 425,‎ 1989, p. 73–90 (DOI 10.1098/rspa.1989.0099, Bibcode 1989RSPSA.425...73D)

[6] Phys. Rév. Un 52 3457-3467 (1995), DOI:10.1103/PhysRevA.52.3457 10.1103; e-print « quant-ph/9503016 », texte en accès libre, sur arXiv.

[7] R. P. Feynman, "mécanique Quantique" ordinateurs, de l'Optique News, février 1985, 11, p. 11; réimprimé dans les Fondations de la Physique 16(6) 507-531.