Point de Bancroft

Figure 2 - Déviations par rapport à la loi de Raoult dans le cas d'un point de Bancroft. L'existence d'un point de Bancroft pour un mélange binaire induit un azéotrope.

On considère un mélange de deux corps ${\displaystyle 1}$ et ${\displaystyle 2}$ à l'équilibre liquide-vapeur. On note respectivement ${\displaystyle P_{1}^{\text{sat}}}$ et ${\displaystyle P_{2}^{\text{sat}}}$ leurs pressions de vapeur saturante à la température ${\displaystyle T}$.

On suppose que les deux corps présentent un point de Bancroft, c'est-à-dire une température ${\displaystyle T_{\text{B}}}$ telle que :

Point de Bancroft : ${\displaystyle P_{1}^{\text{sat}}\!\left(T_{\text{B}}\right)=P_{2}^{\text{sat}}\!\left(T_{\text{B}}\right)=P_{\text{B}}}$

Dans le diagramme de phases liquide-vapeur du mélange binaire à la température ${\displaystyle T_{\text{B}}}$ (diagramme représentant la pression ${\displaystyle P}$ en fonction de la composition, voir figure 2), les courbes d'ébullition et de rosée passent toutes les deux par les points :

• ${\displaystyle \left(x_{1}^{\text{l}}=x_{1}^{\text{g}}=1\,;\,P=P_{1}^{\text{sat}}=P_{\text{B}}\right)}$ lorsque le corps ${\displaystyle 1}$ est pur ;
• ${\displaystyle \left(x_{2}^{\text{l}}=x_{2}^{\text{g}}=1\,;\,P=P_{2}^{\text{sat}}=P_{\text{B}}\right)}$ lorsque le corps ${\displaystyle 2}$ est pur ;

avec :

• ${\displaystyle x_{1}^{\text{l}}}$ et ${\displaystyle x_{1}^{\text{g}}}$ les fractions molaires du corps ${\displaystyle 1}$ respectivement en phase liquide et phase vapeur ;
• ${\displaystyle x_{2}^{\text{l}}}$ et ${\displaystyle x_{2}^{\text{g}}}$ les fractions molaires du corps ${\displaystyle 2}$ respectivement en phase liquide et phase vapeur.

En application de la loi de Raoult, si le mélange était idéal on aurait :

• la courbe d'ébullition idéale : ${\displaystyle P=\left(P_{2}^{\text{sat}}-P_{1}^{\text{sat}}\right)x_{2}^{\text{l}}+P_{1}^{\text{sat}}=P_{\text{B}}}$ ;
• la courbe de rosée idéale : ${\displaystyle P={P_{1}^{\text{sat}}P_{2}^{\text{sat}} \over \left(P_{1}^{\text{sat}}-P_{2}^{\text{sat}}\right)x_{2}^{\text{g}}+P_{2}^{\text{sat}}}=P_{\text{B}}}$.

La droite d'équation ${\displaystyle P=P_{\text{B}}}$ passant par les deux points définis précédemment représente ainsi la courbe d'ébullition et la courbe de rosée du mélange idéal confondues. Cette droite est horizontale dans le diagramme de phases, voir figure 2. En conséquence, à la température de Bancroft un mélange des deux corps se comporte comme un corps pur quelle que soit la composition du mélange.

Cependant tout mélange réel présente un degré de non-idéalité plus ou moins prononcé, quels que soient ses composants. Par conséquent les courbes d'ébullition et de rosée réelles passent par les deux points définis plus haut mais ne se confondent pas avec la droite de Raoult. Aussi, selon le théorème de Rolle, les courbes d'ébullition et de rosée réelles du mélange, qui sont des courbes continues et dérivables, passent chacune obligatoirement par au moins un point auquel la tangente est horizontale, voir figure 2.

Ceci implique que les courbes d'ébullition et de rosée réelles passent chacune forcément par un extrémum (maximum ou minimum). Or, selon le théorème de Gibbs-Konovalov, en un point d'extrémum des courbes d'ébullition et de rosée les compositions des deux phases ne peuvent être qu'identiques.

En conséquence, un point de Bancroft induit nécessairement un azéotrope du mélange binaire à la température du point de Bancroft. Le comportement azéotropique du mélange s'étend à des températures plus ou moins éloignées de la température de Bancroft selon le caractère non idéal plus ou moins prononcé du mélange.

D'autre part, si l'extrémum est un maximum, la pression de l'azéotrope à la température de Bancroft est supérieure à la pression de Bancroft, il s'agit d'un azéotrope positif. Si l'extrémum est un minimum, la pression de l'azéotrope à la température de Bancroft est inférieure à la pression de Bancroft, il s'agit d'un azéotrope négatif.

Figure 3 - Écarts à la loi de Raoult (courbe d'ébullition). Un mélange suffisamment non idéal peut produire un azéotrope sans avoir de point de Bancroft.

On suppose deux corps n'ayant pas de point de Bancroft. Il n'existe aucune température à laquelle les deux corps ont une pression de vapeur saturante commune.

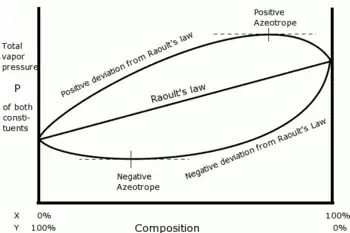
Si le mélange ne présente pas un caractère non idéal trop prononcé, à température donnée les pressions d'ébullition et de rosée du mélange évoluent en fonction de la composition entre les pressions de vapeur saturante des deux corps. Les courbes d'ébullition et de rosée s'écartent de la loi de Raoult mais ne présentent pas d'extrémum : il n'y a pas d'azéotrope.

Si le mélange présente un caractère non idéal suffisamment prononcé, les pressions d'ébullition et de rosée du mélange peuvent prendre des valeurs supérieures à la plus grande des deux pressions de vapeur saturante, ou inférieures à la plus petite des deux pressions de vapeur saturante. Dans ces conditions, les courbes d'ébullition et de rosée présentent nécessairement un extrémum correspondant à un azéotrope selon le théorème de Gibbs-Konovalov, voir figure 3.

Il n'est donc pas nécessaire que le mélange présente un point de Bancroft pour produire un azéotrope, il suffit que le mélange soit suffisamment non idéal.