Octaèdre
En géométrie, un octaèdre (du grec oktô, huit et hedra, face) est un polyèdre à huit faces.
Octaèdre régulier 3D
Présentation
Certains octaèdres satisfont des conditions de symétrie ou de régularité des faces :
- l'octaèdre régulier,
- le prisme hexagonal,
- la pyramide à base heptagonale,
- le tétraèdre tronqué,
- le trapézoèdre tétragonal.
Un octaèdre dont toutes les faces sont triangulaires possède douze arêtes et six sommets.
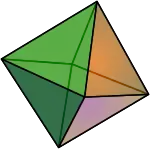Octaèdre régulier
Prisme hexagonal
Tétraèdre tronqué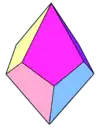
Trapézoèdre tétragonal
L'octaèdre articulé
Il existe des octaèdres flexibles, ce sont les polyèdres déformables de taille minimale. Comme l'a prouvé Cauchy, ils ne peuvent pas être convexes[1].
Notes et références
- Voir Bricard R. Mémoire sur la théorie de l'octaèdre articulé, in Journal de Mathématiques pures et appliquées, Liouville, tome 3:113-148, 1897
Voir aussi
Bibliographie
- (en) H. S. M. Coxeter, Regular Polytopes, New York, Dover Publications, , 3e éd., 321 p. (ISBN 978-0-486-61480-9, LCCN 73084364, lire en ligne), p. 121–122 p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
Articles connexes
- L'octaèdre régulier est un :
- Autres polytopes :
- Polytope
- Hypercube, dual de l'hyperoctaèdre
- n-simplexe
- Cuboctaèdre
Liens externes
- Articles MathWorld (en anglais) :
Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.