Nombre métallique

	⋮
p	p + √4 + p2/2

En mathématiques, les nombres métalliques (ou constantes métalliques) sont des nombres réels permettant d'exprimer les récurrences linéaires du type $u_{n+2}=pu_{n+1}+u_{n}$ .

Ils ont été ainsi nommés par analogie avec le nombre d'or, qui est le premier d'entre eux.

Introduction

Le nombre d'or permettant d'exprimer le terme général des suites $(u_{n})$ vérifiant la récurrence linéaire $u_{n+2}=u_{n+1}+u_{n}$ , il a été proposé d'appeler nombres métalliques les nombres permettant d'exprimer le terme général des suites $(u_{n})$ vérifiant la récurrence linéaire $u_{n+2}=pu_{n+1}+u_{n}$ .

Par définition le p-ième nombre métallique, noté $\varphi _{p}$ est l'unique solution positive de l'équation caractéristique de la récurrence : $x^{2}=px+1$ .

Si une telle suite tend vers l'infini $\varphi _{p}$ est la limite du rapport $u_{n+1}/u_{n}$ .

Pour $p=2$ le métal proposé a été l'argent. Le cuivre (situé au-dessus de l'or et de l'argent dans le tableau périodique), a été proposé pour le nombre suivant (ou le bronze) puis le nickel. [1]^,[2]^,[3] .

Diverses expressions

En tant que solution positive de $x^{2}=px+1$ , on obtient $\varphi _{p}={\frac {p+{\sqrt {p^{2}+4}}}{2}}$ .
Écrivant l'équation sous la forme $x=p+{1 \over x}$ , on obtient la fraction continue : $\varphi _{p}=p+{\cfrac {1}{p+{\cfrac {1}{p+{\cfrac {1}{p+{\cfrac {1}{p+\ddots \,}}}}}}}}=[p;p,\dots ]$ .
Écrivant l'équation sous la forme $x={\sqrt {1+px}}$ , on obtient le radical imbriqué infini $\varphi _{p}={\sqrt {1+p{\sqrt {1+p{\sqrt {1+p{\sqrt {1+\cdots }}}}}}}}$ .
Le p-ième nombre métallique est également donné par une intégrale :
$\varphi _{p}=\int _{0}^{p}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{p+2} \over {2p}}\right)}\,dx.$

Rectangles métalliques

Les trois premiers rectangles métalliques.

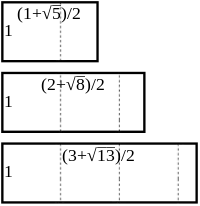
Le p-ième nombre métallique est le rapport longueur=L/largeur=l d'un rectangle tel que si on lui ôte p carrés de taille maximale, on obtient un rectangle semblable à celui de départ.

On obtient en effet la relation ${\frac {l}{L-pl}}={L \over l}$ qui donne $x^{2}=px+1$ si on pose $x=L/l$ .

Premières valeurs

Expressions trigonométriques


Numéro du nombre métallique	1	2	3	4
Formule trigonométrique	$2\cos {\frac {\pi }{5}}$	$\tan {\frac {3\pi }{8}}$	$2\cos {\frac {\pi }{13}}\left({\frac {\sin {\frac {2\pi }{13}}}{\cos {\frac {3\pi }{13}}}}+1\right)$	$8\cos ^{3}{\frac {\pi }{5}}$
Polygone régulier associé	Pentagone	Octogone	Tridécagone	29-gone

Propriétés des puissances entières

Puissances entières

De même que les puissances successives du nombre d'or vérifient $\varphi ^{n}=F_{n}\varphi +F_{n-1}$ où $(F_{n})$ est la suite de Fibonacci,

les puissances des nombres métalliques vérifient :

$\varphi _{p}^{n}=G_{n}\varphi _{p}+G_{n-1}\,\,(1)$

où la suite $(G_{n})$ , définie par $G_{0}=0,G_{1}=1,G_{n+2}=pG_{n+1}+G_{n}$ est la p-suite de Fibonacci.

En prolongeant la suite $(G_{n})$ aux entiers négatifs et en acceptant les $p$ négatifs dans la définition de $\varphi _{p}={\frac {p+{\sqrt {p^{2}+4}}}{2}}$ , la relation (1) est valable pour tous les entiers relatifs.

Alors, si $\varphi '_{p}=\varphi _{-p}=p-\varphi _{p}=-{1 \over {\varphi _{p}}}$ est l'autre solution de $x^{2}=px+1$ , les puissances de $\varphi '_{p}$ vérifient également $\varphi _{p}'^{n}=G_{n}\varphi _{p}'+G_{n-1}$ de sorte que $G_{n}={\frac {\varphi _{p}^{n}-\varphi _{p}'^{n}}{\varphi _{p}-\varphi _{p}'}}$ (généralisation de la formule de Binet).

Remarquons aussi que puisque ${1 \over {\varphi _{p}}}=\varphi _{p}-p$ l'inverse d'un nombre métallique a la même partie fractionnaire que lui.

De plus, la propriété $\varphi _{4}=\varphi ^{3}$ , se généralise. En effet, toute puissance impaire d'un nombre métallique est un autre nombre métallique, la relation précise étant : $\varphi _{p}^{2n+1}=\varphi _{\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}p^{2k+1}}$ ; par exemple $\varphi _{p}^{3}=\varphi _{\left(p^{3}+3p\right)}$ .

Voir également

Notes

A014176, Decimal expansion of the silver mean, 1+sqrt(2).
A098316, Decimal expansion of [3, 3, ...] = (3 + sqrt(13))/2.
A098317, Decimal expansion of phi^3 = 2 + sqrt(5).
A098318, Decimal expansion of [5, 5, ...] = (5 + sqrt(29))/2.
A176398, Decimal expansion of 3+sqrt(10).
A176439, Decimal expansion of (7+sqrt(53))/2.
A176458, Decimal expansion of 4+sqrt(17).
A176522, Decimal expansion of (9+sqrt(85))/2.

Références

Vera W. de Spinadel (1999). The Family of Metallic Means, Vismath 1(3) from Mathematical Institute of Serbian Academy of Sciences and Arts.
de Spinadel, « The Metallic Means and Design », Nexus II: Architecture and Mathematics, Fucecchio (Florence), Edizioni dell'Erba,‎ 1998, p. 141–157 (lire en ligne)
"An Introduction to Continued Fractions: The Silver Means", maths.surrey.ac.uk.

Liens externes

Stakhov, Alexey. " Les mathématiques de l'harmonie: clarifier les origines et le développement des mathématiques ", PeaceFromHarmony.org .
Cristina-Elena Hrețcanu et Mircea Crasmareanu (2013). " Structures métalliques sur les collecteurs riemanniens ", Revista de la Unión Matemática Argentina .
Rakočević, Miloje M. " Généralisation supplémentaire du nombre d'or par rapport à l'équation" divine "d'Euler ", Arxiv.org .

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[4] A014176, Decimal expansion of the silver mean, 1+sqrt(2).

[5] A098316, Decimal expansion of [3, 3, ...] = (3 + sqrt(13))/2.

[6] A098317, Decimal expansion of phi^3 = 2 + sqrt(5).

[7] A098318, Decimal expansion of [5, 5, ...] = (5 + sqrt(29))/2.

[8] A176398, Decimal expansion of 3+sqrt(10).

[9] A176439, Decimal expansion of (7+sqrt(53))/2.

[10] A176458, Decimal expansion of 4+sqrt(17).

[11] A176522, Decimal expansion of (9+sqrt(85))/2.

[1] Vera W. de Spinadel (1999). The Family of Metallic Means, Vismath 1(3) from Mathematical Institute of Serbian Academy of Sciences and Arts.

[2] Spinadel, « The Metallic Means and Design », Nexus II: Architecture and Mathematics, Fucecchio (Florence), Edizioni dell'Erba,‎ 1998, p. 141–157 (lire en ligne)

[3] "An Introduction to Continued Fractions: The Silver Means", maths.surrey.ac.uk.

p	Expression	Écriture décimale	Métal	Suite récurrente associée
1	$1 + \sqrt 5 / 2$	1,618033989	or	suite de Fibonacci
2	$1+{\sqrt {2}}$	2,414213562 [note 1]	argent	suite de Pell
3	$3 + \sqrt 13 / 2$	3,302775638 [note 2]	cuivre ou bronze	suite A006190 de l'OEIS
4	$2+{\sqrt {5}}$	4,236067978 [note 3]		suite A001076 de l'OEIS
5	$5 + \sqrt 29 / 2$	5,192582404 [note 4]		suite A052918 de l'OEIS
6	$3+{\sqrt {10}}$	6,162277660 [note 5]		suite A005668 de l'OEIS
7	$7 + \sqrt 53 / 2$	7,140054945 [note 6]
8	$4+{\sqrt {17}}$	8,123105626 [note 7]
9	$9 + \sqrt 85 / 2$	9,109772229 [note 8]
⋮
p	$p + \sqrt 4 + p 2 / 2$