Nombre étoilé

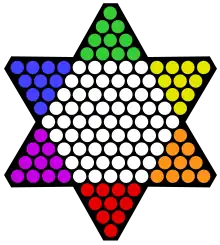
En mathématiques, un nombre étoilé est un nombre figuré polygonal centré qui représente un hexagramme centré, comme le plateau des dames chinoises.

Le 5^e nombre étoilé vaut 121, comme somme de 61 (le 5^e nombre hexagonal centré) et de 60 (six fois le 4^e nombre triangulaire).

Le n-ième nombre étoilé S_n s'exprime simplement en fonction du (n – 1)-ième nombre triangulaire t_n–1 = n(n – 1)/2 : S_n est la somme du n-ième nombre hexagonal centré, qui vaut 1 + 6t_n–1, et de 6 fois t_n–1. Il est donc égal au n-ième nombre dodécagonal centré :

${\displaystyle S_{n}=C_{12,n}=1+12\,t_{n-1}=1+6\,n(n-1).}$

Les 25 premiers nombres étoilés sont 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937, 1 093, 1 261, 1 441, 1 633, 1 837, 2 053, 2 281, 2 521, 2 773, 3 037, 3 313 et 3 601 (suite A003154 de l'OEIS). Cette suite d'entiers est de période 25 modulo 100 et de période 3 modulo 9.

Il existe une infinité d'indices n pour lesquels le n-ième nombre étoilé est triangulaire (suite A003154 de l'OEIS) et une infinité pour lesquels il est carré (suite A054318 de l'OEIS). Dans les deux cas, ce sont les solutions d'une équation diophantienne. Les trois premiers nombres étoilés triangulaires sont S₁ = 1 = t₁, S₇ = 253 = t₂₂ et S₉₁ = 49 141 = t₃₁₃ et les trois premiers nombres étoilés carrés sont S₁ = 1², S₅ = 121 = 11² et S₄₅ = 11 881 = 109².

Les dix plus petits nombres étoilés premiers sont 13, 37, 73, 181, 337, 433, 541, 661, 937 et 1 093 (suite A083577 de l'OEIS).