Hiérarchie de Chomsky
En informatique théorique, en théorie des langages, et en calculabilité, la hiérarchie de Chomsky (parfois appelée hiérarchie de Chomsky-Schützenberger) est une classification des grammaires formelles (et par extension, des langages formels respectifs engendrés par les grammaires), décrite par Noam Chomsky en 1956[1].
Présentation
La hiérarchie introduite par Noam Chomsky repose sur le modèle de grammaire formelle. Il définit les classes de sa hiérarchie comme modèles possibles pour la description des propriétés structurelles des langues naturelles. Noam Chomsky a proposé une classification en quatre types de langages, des type 0 au type 3. Cette terminologie initiale s’est maintenue, mais d’autres noms sont maintenant plus fréquents. Chomsky a présenté ces familles en termes de grammaires formelles, et les diverses classes de grammaires sont définies par des restrictions successives dans la forme des règles.
Une propriété remarquable de la classification de Chomsky est que, pour chaque type, il existe une famille d’automates qui acceptent exactement les langages de ce type. Ces automates varient par la nature et l’emploi de la mémoire auxiliaire. La traduction en classes de complexité est moins nette : les langages rationnels (type 3) sont dans DTIME(n), les langages algébriques (type 2) dans DTIME(n3), les langages contextuels (type 1) en DTIME(nM), où M dépend de la grammaire, mais la réciproque n'est pas vraie.
La classification de Chomsky, reprise dans la presque totalité des manuels d’enseignements de l'informatique, s'est révélée très fructueuse dans ses applications, notamment dans la conception et l’analyse des langages de programmation et la compilation de ces langages. Les langages rationnels et algébriques ont fait l’objet d'études théoriques très poussées par le passé. Les langages contextuels sont surtout employés dans la description de langues naturelles.
Quatre classes de grammaires et de langages
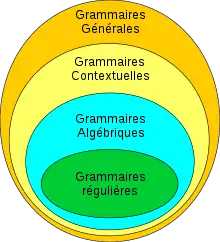
Chomsky a défini quatre classes de grammaires, nommées de type 0 à type 3, et donc aussi quatre classes de langages, engendrés par ces grammaires hiérarchiquement imbriquées:
- Les langages de type 0 sont les plus généraux : ce sont les langages récursivement énumérables.
- Les langages de type 1 sont les langages contextuels, en anglais « context-sensitive ».
- Les langages de type 2 sont appelés langages algébriques ou « hors contexte », en anglais « context-free ».
- Les langages de type 3 sont les langages « réguliers » ou langages rationnels.
Tous les langages de type 3 sont des langages de type 2. Tous les langages de type 2 sont des langages de type 1. Tous les langages de type 1 sont des langages de type 0. La table suivante résume la correspondance entre types de grammaire, langages et machines.
Grammaire Règles de production Langage Machine type 0 récursivement énumérable Machine de Turing type 1 contextuel Automate linéairement borné type 2 algébrique Automate à pile non déterministe type 3 rationnel Automate fini
Dans la présentation formelle ci-dessous, est le vocabulaire de la grammaire, composé des symboles terminaux et non-terminaux, est l'ensemble des symboles non-terminaux, et est le mot vide.
Type 0 : grammaires générales
Aucune restriction n'est imposée aux règles. Elles ont la forme :
Ces grammaires génèrent la classe des langages récursivement énumérables. Ce sont exactement les langages reconnaissables par une machine de Turing. Le problème de l'appartenance d'un mot à un langage de cette classe est indécidable.
Type 1 : grammaires contextuelles
Les règles sont de la forme :
Autrement dit, toute règle comprend un non-terminal entouré de deux mots qui décrivent le contexte dans lequel la variable peut être remplacée. Ces grammaires sont dites contextuelles (en anglais context-sensitive), car le remplacement d'un élément non-terminal peut dépendre des éléments autour de lui : son contexte. Les langages produits, appelés langages contextuels ou sensibles au contexte, sont exactement ceux reconnus par une machine de Turing non déterministe à mémoire linéairement bornée, appelés couramment automates linéairement bornés. D'autres formulations équivalentes existent pour les grammaires définissant les langages contextuels.
Type 2 : grammaires non contextuelles ou algébriques
Les règles sont de la forme :
Une telle règle peut être vue comme une règle contextuelle où le contexte des règles est vide, à condition que le membre droit n'est pas le mot vide. L'adjectif « non contextuel » exprime le fait que les symboles non terminaux sont traités indépendamment de la place où ils apparaissent. Ces grammaires engendrent exactement les langages algébriques, appelés aussi langages hors contexte, langages acontextuels, ou langages non contextuels. Ils sont reconnus par un automate à pile.
Type 3 : grammaires régulières
Les grammaires régulières sont soit les grammaires linéaires à gauche soit les grammaires linéaires à droite :
- Dans les grammaires linéaires à gauche, les règles sont de la forme :
- Dans les grammaires linéaires à droite, les règles sont de la forme :
Les grammaires régulières engendrent les langages rationnels. En effet, une grammaire régulière se transforme facilement en un automate fini (théorème de Kleene).
Attention, on ne peut pas autoriser les deux types de règles simultanément dans une grammaire sans sortir de la classe des langages rationnels : on obtient les grammaires linéaires qui constituent une classe intermédiaire entre le type 2 et le type 3. Les règles d'une grammaire linéaire sont de la forme :
Inclusion des familles
- La classe des langages rationnels (type 3) est incluse strictement dans la classe des langages algébriques (type 2).
- La classe des langages contextuels (type 1) est incluse strictement dans la classe des langages récursivement énumérables (type 0).
- L'inclusion de la classe des langages algébriques (type 2) dans la classe des langages contextuels (type 1) doit être précisée car un langage contextuel ne contient jamais le mot vide ε. L'énoncé exact est :
- Un langage algébrique ne contenant pas le mot vide est un langage contextuel
- ou, de manière équivalente :
- Un langage algébrique est un langage contextuel éventuellement augmenté du mot vide.
Exemples de langages
- Langages réguliers :
. - Langages algébriques qui ne sont pas rationnels :
, l'ensemble des palindromes (qui est même un langage linéaire, comme le précédent), le langage de Dyck - Langages contextuels qui ne sont pas algébriques :
.
Voir aussi les exemples sur la page grammaire formelle. La théorie des langages formels dispose de nombreux outils pour affirmer, ou infirmer, le type d'un langage (rationnel, algébrique etc.). La construction explicite d'une grammaire reconnaissant un langage donné n'est pas toujours facile.
Raffinement de la hiérarchie de Chomsky
La hiérarchie originale de Chomsky comprenait quatre classes. D'autres classes sont souvent intercalées[2],[3],[4] :
- entre le type 0 et le type 1, les langages récursifs, qui sont acceptés par les machines de Turing qui s'arrêtent toujours ;
- entre le type 1 et le type 2, les langages à grammaires indexées, définis par des grammaires plus générales que les grammaires contextuelles ;
- entre le type 2 et le type 3, les langages algébriques déterministes, pour lesquels il existe une caractérisation par automate, mais pas par les grammaires[5] ;
- aussi entre le type 2 et le type 3, les langages linéaires, engendrés par les grammaires linéaires.
Les grammaires d'arbres adjoints[6],[7] définissent une famille entre les langages algébriques et les langages contextuels. Ils sont acceptés par les automates à piles embarquéee[8]. Ces grammaires font partie des grammaires qui permettent de mieux cerner la structure des langues naturelles, regroupés sous le nom langage légèrement sensible au contexte (en)[9].
D'autres raffinements existent, qui montrent que la structure n'est pas « linéaire » : par exemple, si l'on compare les langages linéaires et les langages algébriques déterministes, on s’aperçoit que ces familles ne sont pas contenues l'une dans l'autre.
Extension de cette hiérarchie
La hiérarchie de Chomsky concerne uniquement le domaine du calculable défini paradigmatiquement par ce que peut calculer une machine de Turing. Au-delà existent d'autres hiérarchies de langages dont la hiérarchie arithmétique.
Bibliographie
- Noam Chomsky,
- 1959a On certain formal properties of grammars, Information and Control 2, pp. 137–67.
- 1959b A note on phrase structure grammars, Information and Control 2, pp. 393–95.
- 1962 Context-free grammars and pushdown storage, RLE Quart.Prog. Rept. no 65. Cambridge, Mass., MIT.
- John E. Hopcroft et Jeffrey D. Ullman, Introduction to Automata Theory, Languages and Computation, Addison-Wesley,
- (en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, , 3e éd. (ISBN 978-0-32146225-1)
- Daniel I. A. Cohen, Introduction to Computer Theory, John Wiley & Sons,
- Peter Linz, An introduction to Formal Languages and Automata, Jones and Bartlett, , 3e éd., 410 p. (ISBN 978-0-7637-1422-2, lire en ligne)
Notes et références
- (en) Noam Chomsky, « Three models for the description of language », IRE Transactions on Information Theory, no 2, , p. 113–124 (lire en ligne).
- Cohen 1997, Chap. 30 : The Chomsky Hierarchy.
- Hopcroft et Ullman 1979, Chap. 9 : The Chomsky Hierarchy. La réédition de cet ouvrage en 2001 avec Rajeev Motwani ne comporte plus ce chapitre.
- Linz 2001, Chap. 11.4 : The Chomsky Hierarchy.
- Hopcroft et Ullman 1979, Chap. 10 : Deterministic context-free languages.
- A.K. Joshi, L.S. Levy, et M. Takahashi, « Tree adjunct grammars », Journal of Computer Systems Science, 10(1), 1975.
- Unification-Based Tree Adjoining Grammars.
- (en) K. Vijay-Shanker, « A Study of Tree-Adjoining Grammars », Ph.D. Thesis, University of Pennsylvania, .
- voir aussi : Robert McNaughton, «An insertion into the Chomsky hierarchy?», Jewels are forever, 1999, pages 204-212, et T. Jurdziński, K. Lorys, G. Niemann, F. Otto, «Some results on RWW- and RRWW-automata and their relation to the class of growing context-sensitive languages», Journal of Automata, Languages and Combinatorics, Volume 9 Numéro 4, Octobre 2004.
Articles connexes
- Théorie des automates
- Théorie des langages
- Langage formel
- Grammaire formelle
- Marcel-Paul Schützenberger
- Portail de l'informatique théorique
- Portail de la logique
- Portail de la linguistique