Groupe de Klein

Le groupe de Klein est entièrement défini par le fait que les trois éléments différents de l'élément neutre e ont un ordre égal à 2 (ils sont involutifs), et que le produit de deux distincts d'entre eux est égal au troisième. Ses éléments étant notés ${\displaystyle e,a,b,c}$ et sa loi étant notée multiplicativement, sa table s'écrit :

${\displaystyle \cdot }$	e	a	b	c
e	e	a	b	c
a	a	e	c	b
b	b	c	e	a
c	c	b	a	e

On rencontre les notations : ${\displaystyle \{e,a,b,c\}=K_{4},V,{\text{ou }}V_{4}}$ (${\displaystyle V}$ est l'initiale de Vierergruppe).

• La table étant symétrique, la loi est commutative : ${\displaystyle K_{4}}$ est un groupe abélien.
• La diagonale de e montre que tout élément est son propre symétrique, ce qui équivaut à l'involutivité.
• ${\displaystyle K_{4}}$ n'est pas un groupe simple, ayant pour sous-groupes distingués ${\displaystyle \{e,a\},\{e,b\},\{e,c\}}$.
• ${\displaystyle K_{4}}$ est engendré par deux de ses éléments d'ordre 2, par exemple a et b, les relations minimales étant ${\displaystyle a^{2}=e,b^{2}=e,ab=ba}$.
• Par conséquent tout sous-groupe engendré par deux éléments d'ordre deux qui commutent est isomorphe au groupe de Klein.

• 1) Comme tout groupe, ${\displaystyle K_{4}}$ est isomorphe à un sous-groupe du groupe symétrique d'indice le nombre de ses éléments, ici ${\displaystyle S_{4}}$. On peut prendre pour les trois éléments d'ordre deux les trois produits de deux transpositions disjointes ${\displaystyle s_{1}=(1,2)\circ (3,4),\,s_{2}=(1,3)\circ (2,4),\,s_{3}=(1,4)\circ (2,3)}$. Le groupe ${\displaystyle \{id,s_{1},s_{2},s_{3}\}}$ est alors un sous-groupe distingué de ${\displaystyle S_{4}}$. Et ces permutations étant paires, c'est un sous-groupe distingué du groupe alterné ${\displaystyle A_{4}}$ (${\displaystyle n=4}$ est le seul cas où ${\displaystyle A_{n}}$ n'est pas simple).
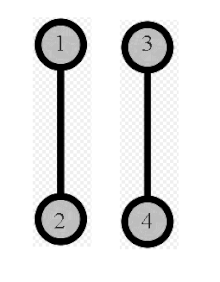
• 2) On peut aussi prendre comme éléments d'ordre deux deux transpositions disjointes et leur produit, par exemple ${\displaystyle t_{1}=(1,2),t_{2}=(3,4),s=(1,2)\circ (3,4)}$. Le groupe ${\displaystyle \{id,t_{1},t_{2},s\}}$ n'est cependant pas distingué dans ${\displaystyle S_{4}}$. Ce groupe est le groupe d'automorphismes du graphe ci-contre (par exemple).
• 3) ${\displaystyle K_{4}}$ est isomorphe à ${\displaystyle C_{2}\times C_{2}=(C_{2})^{2}}$ , produit direct du groupe cyclique d'ordre 2 par lui-même.
  • 3.a) Prenant comme modèle de ${\displaystyle C_{2}}$ le groupe additif ${\displaystyle {\mathbb {Z}}/{2{\mathbb {Z}}}=\{{\overline {0}},{\overline {1}}\}}$ , on obtient la table additive :

La multiplication dans ${\displaystyle {\mathbb {Z}}/{2{\mathbb {Z}}}}$ se transmet à ${\displaystyle ({\mathbb {Z}}/{2{\mathbb {Z}}})^{2}}$ et lui confère une structure d'anneau commutatif d'élément unité ${\displaystyle ({\overline {1}},{\overline {1}})}$. Les deux autres éléments non nuls sont de carré unité et de produit nul (l'anneau n'est donc pas intègre).

• 3.b) Prenant comme modèle de ${\displaystyle C_{2}}$ le groupe multiplicatif ${\displaystyle \{1,-1\}}$, on obtient le groupe multiplicatif de table :

${\displaystyle \times }$	(1,1)	(-1,1)	(1,-1)	(-1,-1)
(0,0)	(1,1)	(-1,1)	(1,-1)	(1,1)
(-1,1)	(-1,1)	(1,1)	(-1,-1)	(1,-1)
(1,-1)	(1,-1)	(-1,-1)	(1,1)	(-1,1)
(1,1)	(1,1)	(1,-1)	(-1,1)	(1,1)

• 3.c) Ce dernier est directement isomorphe au groupe multiplicatif des matrices carrées diagonales d'ordre deux formées de 1 et -1 : ${\displaystyle \left\{{\begin{pmatrix}1&0\\0&1\end{pmatrix}},{\begin{pmatrix}1&0\\0&-1\end{pmatrix}},{\begin{pmatrix}-1&0\\0&1\end{pmatrix}},{\begin{pmatrix}-1&0\\0&-1\end{pmatrix}}\right\}}$.

• 4) Le groupe diédral ${\displaystyle D_{2n}}$ étant isomorphe à ${\displaystyle C_{n}\times C_{2}}$, le groupe de Klein est isomorphe à ${\displaystyle D_{4}}$.

• 5) Le groupe de Klein est isomorphe à plusieurs sous-groupes du groupe à huit éléments ${\displaystyle (C_{2})^{3}}$ ; en effet tous les sous-groupes engendrés par deux éléments non neutres distincts de ${\displaystyle (C_{2})^{3}}$ sont des groupes de Klein. Par exemple, prenant ${\displaystyle {\mathbb {Z}}/{2{\mathbb {Z}}}}$ comme modèle de ${\displaystyle C_{2}}$ :
• 5.a) ${\displaystyle \{({\overline {0}},{\overline {0}},{\overline {0}}),({\overline {1}},{\overline {1}},{\overline {0}}),({\overline {1}},{\overline {0}},{\overline {1}}),({\overline {0}},{\overline {1}},{\overline {1}})\}}$, dont l'équivalent multiplicatif matriciel est
• 5.b) ${\displaystyle \left\{{\text{diag}}(1,1,1),{\text{diag}}(-1,-1,1),{\text{diag}}(-1,1,-1),{\text{diag}}(1,-1,-1)\right\}}$.
• 5.c) ou encore ${\displaystyle \{({\overline {0}},{\overline {0}},{\overline {0}}),({\overline {1}},{\overline {1}},{\overline {1}}),({\overline {1}},{\overline {1}},{\overline {0}}),({\overline {0}},{\overline {0}},{\overline {1}})\}}$, dont l'équivalent multiplicatif matriciel est
• 5.d) ${\displaystyle \left\{{\text{diag}}(1,1,1),{\text{diag}}(-1,-1,-1),{\text{diag}}(-1,-1,1),{\text{diag}}(1,1,-1)\right\}}$
• 5.e) ou encore ${\displaystyle \{({\overline {0}},{\overline {0}},{\overline {0}}),({\overline {0}},{\overline {0}},{\overline {1}}),({\overline {0}},{\overline {1}},{\overline {0}}),({\overline {0}},{\overline {1}},{\overline {1}})\}}$, dont l'équivalent multiplicatif matriciel est
• 5.f) ${\displaystyle \left\{{\text{diag}}(1,1,1),{\text{diag}}(1,1,-1),{\text{diag}}(1,-1,1),{\text{diag}}(1,-1,-1)\right\}}$
• 6) Le groupe de Klein est isomorphe au groupe ${\displaystyle ({\mathbb {Z}}/{8{\mathbb {Z}}})^{*}}$ des éléments inversibles de l'anneau ${\displaystyle {\mathbb {Z}}/{8{\mathbb {Z}}}}$ , d'éléments ${\displaystyle {\overline {1}},{\overline {3}},{\overline {5}}=-{\overline {3}},{\overline {7}}=-{\overline {1}}}$, ainsi qu'à ${\displaystyle ({\mathbb {Z}}/{12{\mathbb {Z}}})^{*}}$ d'éléments ${\displaystyle {\overline {1}},{\overline {5}},{\overline {7}}=-{\overline {5}},{\overline {11}}=-{\overline {1}}}$. Dans les deux autres cas (${\displaystyle n=5,10}$) où ${\displaystyle ({\mathbb {Z}}/{n{\mathbb {Z}}})^{*}}$ possède quatre éléments, il est cyclique.
• 7) Géométriquement, en dimension deux, le groupe de Klein est isomorphe au groupe des isométries laissant globalement invariant un rectangle ou un losange (non carrés), éventuellement réduits à un segment. Les quatre éléments sont alors l'identité id, les deux réflexions ${\displaystyle s_{x},s_{y}}$ selon les médianes, et la symétrie centrale ${\displaystyle s_{O}}$ de centre le centre du polygone, d'où la table :

${\displaystyle \circ }$	id	${\displaystyle s_{x}}$	${\displaystyle s_{y}}$	${\displaystyle s_{O}}$
id	id	${\displaystyle s_{x}}$	${\displaystyle s_{y}}$	${\displaystyle s_{O}}$
${\displaystyle s_{x}}$	${\displaystyle s_{x}}$	id	${\displaystyle s_{z}}$	${\displaystyle s_{y}}$
${\displaystyle s_{y}}$	${\displaystyle s_{y}}$	${\displaystyle s_{O}}$	id	${\displaystyle s_{x}}$
${\displaystyle s_{O}}$	${\displaystyle s_{O}}$	${\displaystyle s_{y}}$	${\displaystyle s_{O}}$	id

Si la figure est un carré, il y a en plus les deux réflexions selon les diagonales et les rotations d'angles ${\displaystyle \pm 90^{\circ }}$, soit 8 éléments qui forment alors le groupe diédral ${\displaystyle D_{8}}$ d'ordre 8.

Passant aux matrices des transformations précédentes, on obtient la représentation matricielle multiplicative vue en 3) c).

• 
  9) En dimension trois, le groupe de Klein est isomorphe au groupe des isométries laissant globalement invariant un parallélépipède rectangle non cubique. C'est pourquoi on l'appelle parfois le groupe (du retournement) du matelas. Les trois éléments involutifs sont les retournements autour des trois axes de symétrie du parallélépipède. Étant notés ${\displaystyle s_{x},s_{y},s_{z}}$, on obtient la table :

${\displaystyle \circ }$	id	${\displaystyle s_{x}}$	${\displaystyle s_{y}}$	${\displaystyle s_{z}}$
id	id	${\displaystyle s_{x}}$	${\displaystyle s_{y}}$	${\displaystyle s_{z}}$
${\displaystyle s_{x}}$	${\displaystyle s_{x}}$	id	${\displaystyle s_{z}}$	${\displaystyle s_{y}}$
${\displaystyle s_{y}}$	${\displaystyle s_{y}}$	${\displaystyle s_{z}}$	id	${\displaystyle s_{x}}$
${\displaystyle s_{z}}$	${\displaystyle s_{z}}$	${\displaystyle s_{y}}$	${\displaystyle s_{x}}$	id

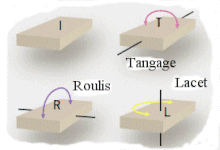
Dans la figure ci-contre, les trois retournements sont nommés d'après leur formulation aéronautique : roulis, tangage, lacet.

Passant aux matrices des transformations précédentes, on obtient la représentation matricielle multiplicative vue en 5.b)

• 10) En dimension trois, le groupe engendré par les trois réflexions par rapport à trois plans orthogonaux deux à deux ${\displaystyle xOy,xOz,yOz}$ forme le groupe à huit éléments ${\displaystyle \{id,s_{xy},s_{xz},s_{yz},s_{x},s_{y},s_{z},s_{O}\}}$ où ${\displaystyle s_{x},s_{y},s_{z}}$ sont les trois retournements vus ci-dessus et ${\displaystyle s_{O}}$ la symétrie centrale de centre O. Ce groupe est isomorphe à ${\displaystyle (C_{2})^{3}}$ de sorte que deux éléments distincts de l'identité engendrent un groupe de Klein. Par exemple ${\displaystyle s_{x},s_{y}}$ engendrent le groupe vu en 9) , ${\displaystyle s_{xy},s_{xz}}$ engendrent ${\displaystyle \{id,s_{xy},s_{xz},s_{x}\}}$ dont l'équivalent matriciel est 5.f), et ${\displaystyle s_{O},s_{z}}$ engendrent ${\displaystyle \{id,s_{O},s_{z},s_{xy}\}}$ dont l'équivalent matriciel est 5.d). Il y a ainsi sept sous-groupe de ${\displaystyle (C_{2})^{3}}$ isomorphes au groupe de Klein.
• 11) Plus généralement, les sous-groupes de Klein de ${\displaystyle (C_{2})^{n}}$ correspondent aux sous-espaces vectoriels de dimension deux du ${\displaystyle ({\mathbb {Z}}/{2{\mathbb {Z}}})}$ - espace vectoriel ${\displaystyle ({\mathbb {Z}}/{2{\mathbb {Z}}})^{n}}$ ; leur nombre est donc le coefficient binomial de Gauss ${\displaystyle {n \choose 2}_{2}={\frac {(2^{n}-1)(2^{n}-2)}{6}}}$.
• 12) Le groupe de Klein est aussi isomorphe à l'ensemble des parties d'un ensemble à deux éléments ${\displaystyle \{a,b\}}$, muni de la différence symétrique. Ce qui donne la table :

${\displaystyle \Delta }$	${\displaystyle \varnothing }$	${\displaystyle \{a\}}$	${\displaystyle \{b\}}$	${\displaystyle \{a,b\}}$
${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \{a\}}$	${\displaystyle \{b\}}$	${\displaystyle \{a,b\}}$
${\displaystyle \{a\}}$	${\displaystyle \{a\}}$	${\displaystyle \varnothing }$	${\displaystyle \{a,b\}}$	${\displaystyle \{b\}}$
${\displaystyle \{b\}}$	${\displaystyle \{b\}}$	${\displaystyle \{a,b\}}$	${\displaystyle \varnothing }$	${\displaystyle \{a\}}$
${\displaystyle \{a,b\}}$	${\displaystyle \{a,b\}}$	${\displaystyle \{b\}}$	${\displaystyle \{a\}}$	${\displaystyle \varnothing }$

La loi "intersection" confère alors à ${\displaystyle (P(\{a,b\}),\Delta ,\cap )}$ la structure d'anneau commutatif d'élément unité ${\displaystyle \{a,b\}}$, anneau isomorphe à l'anneau vu en 3) a).

• 13) Le polynôme ${\displaystyle P=1+X+X^{2}}$ étant irréductible sur le corps à deux éléments ${\displaystyle F_{2}}$, le quotient ${\displaystyle F_{2}(X)/P}$ est un corps qui se trouve avoir 4 éléments ${\displaystyle {\overline {0}},{\overline {1}},{\overline {X}}=\varphi ,\varphi ^{2}={\overline {1}}+\varphi }$ et dont la partie additive est le groupe de Klein. Ici, les deux éléments non nuls différents de l'élément unité sont inverses l'un de l'autre. On a les tables :

+ 0 1 φ φ² 0 0 1 φ φ² 1 1 0 φ² φ φ φ φ² 0 1 φ² φ² φ 1 0

${\displaystyle \times }$ 0 1 φ φ² 0   0   0 0 0 1 0 1 φ φ² φ 0 φ φ² 1 φ² 0 φ² 1 φ

Dans Les Structures élémentaires de la parenté, l’ethnologue Claude Lévi-Strauss, aidé du mathématicien André Weil, dégage le concept de structure élémentaire de parenté en utilisant la notion de groupe de Klein[2]. Dans La Structure des mythes, Lévi-Strauss réutilisera les groupes de Klein pour établir la formule canonique du mythe.

• Portail des mathématiques