Droite de Henry
La droite de Henry est une méthode graphique pour ajuster une distribution gaussienne à celle d'une série d'observations (d'une variable numérique continue). En cas d'ajustement, elle permet de lire rapidement la moyenne et l'écart type d'une telle distribution.
Pour les articles homonymes, voir Henry.

Cette droite porte le nom du polytechnicien P.J.P. Henri (ou Henry) (1848 - 1907) qui l'a mise au point et en a enseigné l'utilisation à l'école d'artillerie dans les années 1880. Jules Haag, par la suite l'introduisit dans son cours à l'école d'artillerie de Fontainebleau[1]. C'est une méthode voisine de la technique du Diagramme Quantile-Quantile appliquée aux distributions normales.
Principe
Si X est une variable gaussienne de moyenne x et de variance σ2, et si N est une variable de loi normale centrée réduite, on a les égalités suivantes :
- , avec
(on note Φ la fonction de répartition de la loi normale centrée réduite).
Pour chaque valeur xi de la variable X, on peut, à l'aide d'une table de la fonction Φ :
- calculer P(X < xi) ;
- en déduire ti tel que Φ(ti) = P(X < xi).
Si la variable est gaussienne, les points de coordonnées (xi ; ti) sont alignés sur la droite d'équation
- .
On compare donc les valeurs des quantiles de la loi empirique (xi) aux quantiles de la loi normale centrée réduite ti.
Cette méthode peut également se généraliser à d'autres distributions en comparant là encore les quantiles théoriques aux quantiles empiriques ; on parle parfois de « tracé quantile-quantile ».
Exemple numérique
Lors d'un examen noté sur 20, on obtient les résultats suivants :
- 10 % des candidats ont obtenu moins de 4
- 30 % des candidats ont obtenu moins de 8
- 60 % des candidats ont obtenu moins de 12
- 80 % des candidats ont obtenu moins de 16
On cherche à déterminer si la distribution des notes est gaussienne, et, si oui, ce que valent son espérance et son écart type.
On connaît donc 4 valeurs xi, et, pour ces 4 valeurs, on connaît P(X < xi).
En utilisant la table de la fonction de répartition de la loi normale centrée réduite, on détermine les ti correspondants :
| xi | P(X<xi) = Φ(ti) | ti |
| 4 | 0,10 | -1,28 |
| 8 | 0,30 | -0,524 |
| 12 | 0,60 | 0,253 |
| 16 | 0,80 | 0,842 |
Il suffit alors de tracer les points de coordonnées (xi ; ti).
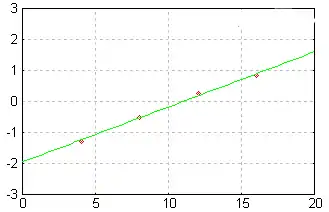
Les points paraissent alignés ; la droite coupe l'axe des abscisses au point d'abscisse 11 et le coefficient directeur 1/σ est (0,842 +1,28)/12 environ, ce qui donnerait un écart type σ de 12/2,12 = 5,7.
Cela laisse penser que la distribution est gaussienne de paramètres (m, σ2) avec m = 11 et σ = 5,7.
Papier gausso-arithmétique
Dans le principe décrit précédemment, il est nécessaire de rechercher les ti correspondant à chaque P(x < xi), ce qui demande une lecture à l'envers de la table de la loi normale. Il est possible aussi de travailler sur un papier dont l'échelle en ordonnée utilise déjà cette conversion. En ordonnée, apparaissent deux graduations :
- à droite, une graduation arithmétique et
- à gauche les valeurs de Φ(t) correspondantes.
On place alors les points grâce à l'échelle de gauche.
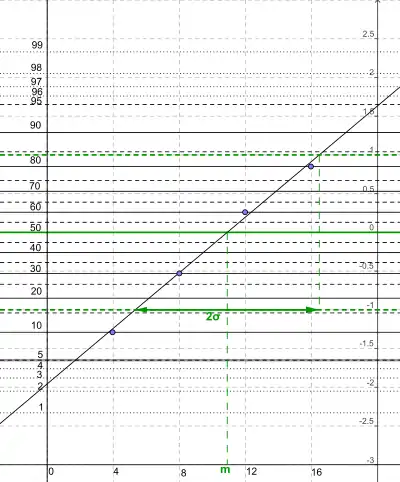
Cette représentation graphique fournit très naturellement la moyenne qui correspond, pour une loi normale, à la médiane c'est-à-dire à l'abscisse du point d'ordonnée 50. Mais elle fournit aussi assez facilement l'écart type en utilisant les intervalles de confiance. Dans une distribution normale, de moyenne m et d'écart-type σ l'intervalle [m - σ ; m + σ] regroupe 68 % de la population. Il y a donc 16 % des valeurs inférieures à m - σ et 84 % des valeurs inférieures à m + σ. On lit donc
- la valeur m - σ comme l'abscisse du point d'ordonnée 16 et
- la valeur m + σ comme celle du point d'ordonnée 84.
L'écart entre ces deux abscisses permet de déterminer la valeur 2σ.
Ainsi, dans le graphique ci-dessous, la moyenne est d'environ 11 et l'écart-type est de (16,7 - 5,2)/2 soit environ 5,7.
Annexes
Notes et références
- Michel Armatte, Robert Gibrat et la loi de l'effet proportionnel, dans Mathématiques et sciences humaines, tome 129 (1995), p 16
Liens externes
- [PDF] Droite de Henry , échelle gausso-arithmétique et exercices
- [PDF] Comment construire un diagramme de Henry avec Excel et comment l'interpréter
- Droite de Henry sous MATLAB, aucune toolbox requise
- Portail des probabilités et de la statistique