Code de Gauss

Dans un article de 1823[1], Gauss se proposait de démontrer qu’une courbe plane fermée de nombre d'enroulement ${\displaystyle N}$ (nombre de tours sur lui-même effectué par un observateur parcourant la courbe) possède au moins ${\displaystyle N-1}$ croisements (${\displaystyle N\geqslant 1}$).

À l'occasion de cette démonstration, il a introduit le code qui porte son nom, défini dans le paragraphe suivant.

Comme visualisé ci-contre, une courbe circulaire à ${\displaystyle n(=3)}$ boucles internes a un nombre d'enroulement égal à ${\displaystyle N=n+1(=4)}$ ; elle possède le nombre minimal de croisements à ${\displaystyle N}$ donné.

Par courbe, on entend ici une courbe fermée, ayant une tangente en tous points, et dont les points multiples, en nombre fini, sont tous doubles et transverses (tangentes non confondues), qui seront ici dénommés croisements. Cela équivaut topologiquement à un graphe planaire 4-régulier (4 arêtes partant de chaque sommet), les croisements correspondant aux sommets du graphe (par graphe, on entend graphe non orienté et acceptant les arêtes multiples). Notons que s'il y a ${\displaystyle n}$ croisements, il y a alors ${\displaystyle 2n}$ arêtes, donc par la relation d'Euler, ${\displaystyle n+2}$ faces (en comptant la face externe).

Deux courbes sont dites équivalentes, si elles sont images l'une de l'autre par un difféomorphisme du plan.

Ayant numéroté arbitrairement de 1 à ${\displaystyle n}$ ces croisements, et ayant choisi arbitrairement un point de départ sur la courbe, et un sens de parcours, le code de Gauss de la courbe est alors la liste des ${\displaystyle 2n}$ numéros des croisements que l'on obtient successivement lorsqu’on effectue un parcours complet sur la courbe.

On trouvera dans la figure ci-dessous les codes de Gauss des courbes correspondant aux projections des nœud de trèfle et nœud de huit. On peut noter que les deux courbes du haut ont le même code de Gauss, mais ne sont pas équivalentes dans le plan (elles le sont par contre sur la sphère).

Un code de Gauss est toujours une liste de 2${\displaystyle n}$ nombres entre 1 et ${\displaystyle n}$, chacun étant répété deux fois, que nous désignerons par mot de Gauss. Notons que le nombre de mots de Gauss est le coefficient multinomial ${\displaystyle {\binom {2n}{2,2,...,2}}=(2n)!/2^{n}}$.

• 
  Courbe à 7 croisements avec son code et son diagramme de Gauss.
• 
  Codes de Gauss de courbes à 3 ou 4 croisements.
• 
  Les 3,5,15 courbes à respectivement 3,4,5 croisements répertoriées par Nagy.

Les 1,1,3, et 5 diagrammes de Gauss réalisables pour n=1, 2,3, et 4 avec des courbes correspondantes ; pour n = 4, les dessins sont de la main de Gauss.

On peut visualiser un code de Gauss en traçant un cercle, marquant des points successifs numérotés par les nombres du code, et reliant par une corde les points de même numéro, le dessin obtenu étant dénommé diagramme de Gauss (ou diagramme de cordes). L’intérêt étant qu'à une rotation près ou une symétrie près, le diagramme ne dépend plus de la numérotation des croisements ni du sens de parcours.

Nota : le nombre de diagrammes de Gauss à rotation près est donné par suite A007769 de l'OEIS, et à rotation et symétrie près par suite A054499 de l'OEIS.

Un mot (ou diagramme) de Gauss est dit réalisable s'il provient d'une courbe au sens ci-dessus. Gauss s'est posé le problème de caractériser cette réalisabilité, et a trouvé la condition nécessaire très simple suivante :

Dans un mot de Gauss réalisable, deux nombres égaux sont séparés par un nombre pair de nombres.

Par exemple, le mot (1,2,1,3,3,2) n'est pas réalisable car les deux 1 sont séparés par un seul nombre.

Pour un diagramme de Gauss, la condition se traduit par le fait que de part et d'autre d'une corde, il y a un nombre pair de points marqués.

Cette condition a été démontrée par Julius Nagy en 1927[2].

On notera l'utilisation du théorème de Jordan dans la démonstration : sur un tore par exemple, on peut trouver une courbe qui aurait pour code (1,2,1,2).

Malheureusement, Gauss avait déjà remarqué ([1] page 284) qu'à partir de n = 5, cette condition de parité n'est pas suffisante ; par exemple le mot (1,2,3,4,5,3,4,1,2,5) vérifie la condition de parité mais ne correspond à aucune courbe à 5 croisements.

Plusieurs mathématiciens ont donné et démontré des conditions nécessaires et suffisantes de réalisabilité : Nagy en 1927[2], Dehn en 1936[4], Treybig en 1968[5], Marx en 1969[6], Bouchet en 1972[7], Lovasz en 1976[8], Rosenstiehl en 1976[9], Chaves et Weber en 1994[10], Burckel dans les années 1990[11], et Grindblat-Lopatkin en 2017[12].

Rosenstiehl, par exemple, définit le graphe d'entrelacements G associé au mot de Gauss, dont les sommets sont les nombres de 1 à n, deux nombres a et b étant reliés par une arête s'ils sont entrelacés dans le mot : entre les deux occurrences de a, le nombre b apparait une fois et une seule (et donc entre les deux occurrences de b, a apparait une fois et une seule). Il démontre que le mot de Gauss est réalisable si et seulement si :

1) Les sommets de G sont de degré pair (condition de Gauss).

2) Si {a,b} n'est pas une arête de G, les sommets à la fois reliés à a et b sont en nombre pair.

3) Les arêtes {a,b} de G pour lesquelles les sommets à la fois reliés à a et b sont en nombre pair forment l'ensemble des arêtes incidentes à un même sommet (ou cocycle).

• 
  Courbe à 6 croisements de code de Gauss : (1,2,4,6,5,4,2,1,3,5,6,3)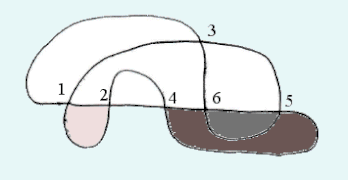
• 
  Courbe reconstituée à partir du code de Gauss précédent.
• 
  Réalisation de la courbe de code Gauss (1,2,1,2) sur le tore.
• 
  Tentative de reconstitution dans le plan du code de Gauss (1,2,3,4,5,3,4,1,2,5) faisant apparaitre 3 croisements supplémentaires.
• 
  Réalisation de la courbe de code de Gauss (1,2,3,4,5,3,4,1,2,5) sur le tore et le plan projectif.

Il s'agit en fait d'un problème similaire à celui de tracer un graphe planaire connaissant les sommets et les arêtes. En effet, si le code de Gauss est ${\displaystyle (x_{1},x_{2},...,x_{2n})}$, les 2${\displaystyle n}$ arêtes du graphe associé à la courbe sont les ${\displaystyle \left\{x_{i-1},x_{i}\right\}}$, plus ${\displaystyle \left\{x_{2n},x_{1}\right\}}$. On place donc ${\displaystyle n}$ croix représentant les croisements numérotés de 1 à ${\displaystyle n}$, que l'on relie par des arêtes qui ne doivent pas se croiser. La contrainte est, lorsqu'on arrive à une croix, de repartir sur la même branche de la croix. Cette contrainte est importante, car par exemple le mot (1,2,1,2) n'est pas réalisable, bien qu'il existe un graphe planaire ayant pour arêtes {1,2},{2,1},{1,2} et {2,1} !

Le site knotilus possède une application permettant de reconstituer automatiquement la courbe (ou plutôt, le nœud alterné) à partir du code de Gauss.

Ci-dessus, on verra une tentative de reconstituer une courbe associée au mot (1,2,3,4,5,3,4,1,2,5) , ce qui est impossible sans croisement dans le plan. À droite, réalisation de ce même code sur le tore et le plan projectif.

Notation de Dowker (2,6,8,4)

Code de Gauss (1,1,2,3,4,2,3,4)

La notation de Dowker[13]^,[14] constitue une autre manière de coder une courbe : ayant de nouveau choisi arbitrairement un point de départ sur la courbe et un sens de parcours, on numérote successivement les ${\displaystyle n}$ croisements par les nombres de 1 à 2${\displaystyle n}$ ; chaque croisement reçoit donc une paire de nombres entre 1 et 2${\displaystyle n}$, et la propriété de parité de Gauss indique que chaque paire est formée d'un nombre pair et d'un nombre impair. La notation de Dowker est alors la liste des nombres pairs associés aux nombre impairs 1, 3, ...,2n-1, dans cet ordre. Par exemple les croisements de la courbe ci-contre, reçoivent les paires successives {1,2},{3,6},{4,7}, et {5,8} ; la liste des impairs (1,3,5,7) est donc associée à la liste des pairs (2,6,8,4) qui constitue une notation de Dowker de la courbe. On récupère un code de Gauss de la courbe en mettant deux 1 aux places 1 et 2, deux 2 aux places 3 et 6, deux 3 aux places 5 et 8, et deux 4 aux places 7 et 4 : (1,1,2,3,4,2,3,4).

Notons que Gauss avait déjà introduit cette notation, en numérotant de 0 à 2n-1 au lieu de 1 à 2n ([1] page 284).

Pour une courbe à n croisements données, il y a au plus 4n notations de Dowker possibles (dues aux 2n points de départ situés sur les 2n arêtes et aux deux sens de parcours), éventuellement confondues. La notation qui a l'ordre lexicographique minimal est dite standard.

Notations de Dowker standards des courbes associées aux quatre premiers nœuds premiers.

Entrelacs de code de Gauss {(1,-2,7,-5,3,-1,2,-3,4,-6),(-4,5,-7,6)} ; si le nœud vert (de trèfle) était seul, il aurait pour code (1,-2,3,-1,2,-3).

Un diagramme d'un nœud est une projection plane du nœud ayant les propriétés des courbes définies ci-dessus, avec en sus l'indication des passages dessus, ou dessous. Le code de Gauss du nœud (ou plutôt de son diagramme) est alors le code de Gauss de cette courbe, les nombres étant affectés du signe plus en cas de passage au-dessus, et du signe moins en cas de passage en dessous. Le code de Gauss est donc formé des 2${\displaystyle n}$ nombres de 1 à ${\displaystyle n}$ et de ${\displaystyle -n}$ à ${\displaystyle -1}$. Pour un entrelacs, on effectue ceci pour chaque brin ; mais attention : pour chaque brin, les croisements avec les autres brins interviennent !

Notons que la condition de parité de Gauss permet de justifier que toute courbe est le diagramme d'un nœud dit "alterné" (où les passages dessus et dessous se suivent de façon alternée) : si dans un croisement donné on a un "pont", lorsqu'on reviendra à ce même croisement, on aura forcément un "souterrain". Par contre, il existe des nœuds dont aucune projection n'est alternée, comme le nœud premier 8.19.

• Code de Gauss dans wikipedia anglophone.
• Notation de Dowker dans wikipedia anglophone.
• Lien entre notation de Dowker et problème des ménages.

Cours sur le sujet par Jeff Erickson.

• Portail des mathématiques