Arc sinus

Comme dérivée d'une bijection réciproque, arcsin est dérivable sur ]–1, 1[ et vérifie ${\displaystyle \arcsin 'x={\frac {1}{\sqrt {1-x^{2}}}}}$.

Cette formule s'obtient grâce au théorème sur la dérivée d'une bijection réciproque et à la relation ${\displaystyle \cos(\arcsin x)={\sqrt {1-x^{2}}}}$.

Si ${\displaystyle |z|\leq 1}$,

${\displaystyle {\begin{aligned}\arcsin z&=z+{\frac {1}{2}}\cdot {\frac {z^{3}}{3}}+{\frac {1\cdot 3}{2\cdot 4}}\cdot {\frac {z^{5}}{5}}+{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\cdot {\frac {z^{7}}{7}}+\dots \\&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}\cdot {\frac {z^{2n+1}}{2n+1}}\\&=\sum _{n=0}^{\infty }{\frac {{\binom {2n}{n}}z^{2n+1}}{4^{n}(2n+1)}}.\end{aligned}}}$

(Voir aussi Fonction hypergéométrique#Cas particuliers.)

Cette fonction peut s'écrire sous la forme d'une intégrale indéfinie :

${\displaystyle \arcsin x=\int _{0}^{x}{\frac {1}{\sqrt {1-t^{2}}}}\,\mathrm {d} t}$.

Les primitives de l'arc sinus s'obtiennent par intégration par parties :

${\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}+C}$.

arccos(x) (bleu) et arcsin(x) (rouge)

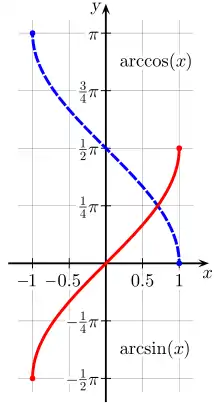
Pour tout réel x entre –1 et 1 : ${\displaystyle \arccos x+\arcsin x={\frac {\pi }{2}}}$.

On peut exprimer la fonction arc sinus avec un logarithme complexe :

${\displaystyle \arcsin x=-{\rm {i}}\ln \left({\rm {i}}x+{\sqrt {1-x^{2}}}\right)}$.