Œuvre scientifique de Lazare Carnot

Cet essai, élaboré par Carnot, est construit sur trois définitions. Chacune est une innovation dans son domaine. La première concerne le mouvement. Carnot l’appelle mouvement géométrique et représente la symbiose entre le mouvement et la géométrie pour une meilleure utilisation de la machine.

Le deuxième terme concerne la force qui est divisée en force sollicitante et force résistante. Pour Carnot, le concept de force n’induit pas seulement une action mécanique indéterminée mais fait le lien entre la cause et son effet mécanique dans les machines. Par conséquent, il convient de faire une distinction entre les différentes forces.

Le troisième paramètre est nommé le moment d’activité, lequel pourrait se définir comme la force qu’on utiliserait effectivement pour produire un travail utile. Carnot compris fort bien que l’utilisation des machines devait servir le progrès et non alimenter les foires en matière de curiosités.

À partir de ces définitions, Carnot parvient à simplifier considérablement le fonctionnement théorique de la machine. Son but, par cette simplification, est de faciliter la compréhension de l’état du système à un moment donné (il est toujours dans l’optique éducative). En fait, c’est le début de la modélisation système :

« A l’aide de ces définitions, je parviens à des propositions qui sont très simples ; je les déduis d’une même équation fondamentale, (…) » (Préface) « Je tire facilement de cette équation un principe général d’équilibre et de mouvement dans les machines proprement dites, (…) » (Préface)

Pourquoi cet essai ?

Dans sa préface, Carnot explique les raisons qui l’ont conduit à écrire un essai sur les machines. Au XVIII^e siècle, une multitude de machines avaient été inventées. Les procédés utilisés (bricolage) et l’imagination des mécaniciens avaient pris le pas sur la méthode scientifique et le savoir technique. La motivation était telle que certains étaient convaincus qu’ils pouvaient réaliser une machine qui amplifierait l’effet ! Or, pour Carnot, le problème des mécaniciens découlait surtout de la recherche d’une illusion qui leur faisait croire qu’en inventant une nouvelle machine ils pourraient dépasser les lois de la physique. C’est la raison pour laquelle, au début de son essai, il répond à la question suivante : qu’est-ce que c’est qu’une machine ? Pour remédier à cette hystérie, Carnot conseille aux responsables d’expliquer aux étudiants mécaniciens qu’il faut toujours partir d’un principe de base, lequel est : on perd toujours en temps ou en vitesse ce qu’on gagne en force. Ce principe qui décrit le fonctionnement du levier est valable pour les machines connues ou le sera toujours pour toutes les machines possibles.

C’est dans ce contexte qu’il faut comprendre le passage suivant :

« (…) tout le monde répète que dans les machines en mouvement on perd toujours en temps ou en vitesse ce qu’on gagne en force ; mais après la lecture des meilleurs éléments de mécanique, qui semble être la vraie place où doivent se trouver la preuve et l’explication de ce principe, son étendue et même sa vraie signification sont-elles faciles à saisir ?

Système levier

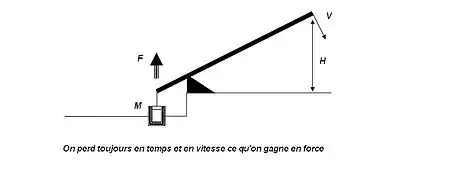
Sa généralité a-t-elle, pour la plupart des lecteurs, cette évidence irrésistible qui doit caractériser les vérités mathématiques ? S’ils éprouvaient cette conviction frappante, ne verrait-on pas des mécaniciens instruits de ces ouvrages, renoncer incessamment à leurs projets chimériques ? Ne cesseraient-ils pas de croire ou de soupçonner de moins, malgré tout ce qu’on leur dit, qu’il y a dans les machines quelque chose de magique ? Les preuves qu’on leur donne du contraire ne s’étendent qu’aux machines simples ; ne croient-ils pas celles-ci capables d’un grand effet; mais on ne leur fait pas voir qu’il doit en être de même dans tous les cas imaginables, et l’on se contente d’une analogie : voilà pourquoi ces mécaniciens espèrent toujours que leur sagacité leur fera découvrir quelque ressource inconnue, quelque machines qui ne soit pas comprise dans les règles ordinaires ; ils se croient d’autant plus surs de la rencontrer, qu’ils s’éloignent davantage de tout ce qui paraît avoir de la relation avec les machines usitées, parce qu’ils s’imaginent que la théorie établie pour celles-ci, ne peut s’étendre à des constructions qui leur semblent n’y avoir aucun rapport ; c’est en vain qu’on leur dit que toute machine se réduit au levier : cette assertion est trop vague et trop tirée, pour qu’on s’y rende sans un examen profond ; ils ne peuvent se persuader que des machines qui paraissent n’avoir rien de commun avec celles qu’on nomme simples, soient sujettes à la même loi, ni qu’on puissent prononcer sur l’inutilité d’un secret dont ils n’ont pas fait de confidence à personne : de là vient que les idées les plus bizarres, les plus éloignées de la simplicité si avantageuse aux machines, sont celles qui leur fournissent le plus d’espoir. Le moyen de déraciner cette erreur, est sans doute de l’attaquer dans sa source même, en montrant que non seulement dans toutes les machines connues, mais encore dans toutes les machines possibles, c’est une loi inévitable(...)» (Préface)

Dans la préface de son essai Carnot s’élève avec force contre ceux qui croient dans le mouvement perpétuel. « Les réflexions que je propose sur cette loi, me conduisent à dire un mot du mouvement perpétuel, et je fais voir non seulement que toute machine abandonnée, à elle-même doit s’arrêter, mais j’assigne l’instant même où cela doit arriver. »

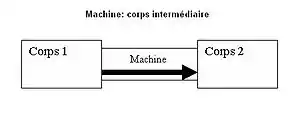
Qu’est-ce qu’une machine ?

Dans un premier temps Carnot explique ce qu’est une machine. Une machine est un corps intermédiaire entre deux corps agissant l’un sur l’autre. Plus précisément, c’est un système faisant le transfert de la force ou du mouvement entre deux corps en retenant une partie et en transférant l’autre partie. Le problème, souligne Carnot, est qu’avec le temps, pour les finalités de recherche, on a tout simplement négligé la masse de ce corps intermédiaire car on a imaginé que l’inertie de la machine n’intervenait que très peu dans le processus de transfert. Naturellement la généralisation de cette "habitude" dans les sciences de la mécanique a fait que le nom de machine a été appliqué pour chaque système d’objet sans inertie car il n’entrait pas dans le calcul général.

Si nous analysons correctement le passage sur le principe du levier et le passage sur la définition de la machine ci-après, nous pouvons « sentir » l’influence de Lazare sur son fils et tenter de comprendre le cheminement mental qui a conduit le jeune Nicolas Léonard Sadi Carnot à découvrir les lois de la thermodynamique notamment et surtout de la deuxième loi. La compréhension de la découverte d’une loi est quelquefois plus importante que sa découverte.

Le moulin et les machines

« Lorsqu’un corps agit sur un autre, c’est toujours immédiatement ou par l’entremise de quelques corps intermédiaire ; ce corps intermédiaire est en général ce qu’on appelle une machine :le mouvement que perd à chaque instant chacun des corps appliqués à cette machine, est en partie absorbé par la machine même, et en partie reçu par les autres corps du système; mais comme il peut arriver que l’objet de la question soit uniquement de trouver l’action réciproque des corps appliqués aux corps intermédiaires, sans qu’on ait besoin d’en connaître l’effet sur le corps intermédiaire même, on a imaginé, pour simplifier la question, de faire abstraction de la masse même de ce corps, en lui conservant d’ailleurs toutes les autres propriétés de la matière : dès lors la science des machines est devenue en quelque sorte une branche isolée de mécanique, dans laquelle il s’agit de considérer l’action réciproque des différentes parties d’un système de corps, parmi lesquelles il s’en trouve qui, privées de l’inertie commune à toutes parties de la matière telle qu’elle existe dans la nature, ont retenu le nom de machines. » page 24 paragraphe 9

La machine a une inertie

Évidemment, dans certains cas, pour les commodités de calcul, on avait pris l’habitude de ne pas tenir compte de l’inertie de la machine car la théorie des machines était devenue assez complexe. L’assemblage d’objet que constituait la machine comportait aussi un assemblage de connaissances théoriques dont on ignorait leurs influences mutuelles. Le recours à la figure particulière de chaque objet qui constituait l’intérieur de la machine n’était pas suffisant pour avoir une idée d’ensemble avec les propriétés mécaniques. Pour cette raison Carnot avait décidé de simplifier le système en arrêtant de considérer différentes natures dans un système de corps. Ainsi le travail de Carnot consistait à rendre leur force d’inertie aux machines pour qu’elles interviennent enfin comme un seul dans le calcul du processus du rendement, par exemple.

La machine selon Carnot

« Cette abstraction pouvait simplifier dans certains cas particuliers, où les circonstances indiquaient ceux des corps dont il convenait de négliger la masse, pour arriver plus facilement au but ; mais on conçoit que la théorie des machines est devenue réellement plus compliquée qu’auparavant ; car alors cette théorie était enfermée dans celle du mouvement des corps tels que la nature nous les offres ; mais à présent il faut considérer à la fois deux sortes de corps, les uns tels qu’ils existent réellement, les autres dépouillés en partie de leurs propriétés naturelles ; or, il est clair que le premier de ces problèmes est un cas particulier de celui-ci ; donc celui-ci est plus compliqué que l’autre : aussi, quoiqu’on parvienne aisément par de pareilles hypothèses à trouver les lois de l’équilibre et du mouvement dans chaque machine particulière, telle que le levier, le treuil, la vis, il en résulte un assemblage de connaissances dont la liaison est difficilement apercevable, et seulement par une espèce d’analogie ; ce qui doit nécessairement arriver tant qu’on aura recours à la figure particulière de chaque machine, pour démontrer une propriété qui lui est commune avec toutes les autres : ces propriétés qui lui est communes étant celles que nous avons vues dans cet essai, il est clair que nous ne parviendrons à les trouver, qu’en faisant abstraction des formes particulières ; commençons donc par simplifier l’état de la question, en cessant de considérer dans un même système des corps différentes nature : rendons enfin aux machines leur force d’inertie ; il nous sera facile, après cela, d’en négliger la masse dans le résultat : nous serons maîtres d’y avoir égard ou non ; et partant, la solution du problème sera aussi générale, en même temps qu’elle sera plus simple. » page 25 paragraphe 10

Ensuite Carnot explique sa méthode pour permettre la simplification du fonctionnement de la machine. Il imagine une verge incompressible et un fil inextensible et donne des exemples dans lesquels on peut remplacer les phénomènes mécaniques par ces verges et fils. Il donne un exemple : soit dans un système, deux corps qui se poussent. Leur impénétrabilité qui les empêche de se rapprocher plus, peut être modélisée par une verge incompressible et leur connexion par une mécanique quelconque peut-être modélisée par un fil inextensible.

"(…) car, lorsque deux corps se choquent, se poussent, ou tendent en général à se rapprocher l’un de l’autre sans pouvoir le faire, à cause de leur impénétrabilité, on peut concevoir entre les deux une petite verge incompressible, et supposer que le mouvement se transmet de l’un à l’autre suivant cette verge ; et de même si deux corps tendent à se séparer, on peut concevoir qu’ils sont retenus l’un à l’autre par un petit fil inextensible, suivant lequel se propage le mouvement ;(…) » page 29 paragraphe 14

« Le but qu’on se propose, en imprimant un mouvement géométrique, est de changer l’état du système, sans cependant altérer l’action réciproque des corps qui le composent, afin de se procurer par-là des rapports entre ces forces exercées et inconnues, et les vitesses arbitraires que prennent les corps, en vertu de ces différents mouvements géométriques (…)" page 41

Qu’est-ce que le mouvement géométrique ?

En fait, le mouvement géométrique est une dynamique qui respecte la construction de la machine. Ce mouvement se définit par son intégration dans la machine par la symbiose. Comme son nom l’indique, ce mouvement est relié à la géométrie et ce n’est pas par hasard. En effet, Carnot est convaincu que la compréhension correcte des machines et leurs fonctionnements passe par la géométrie.

« D’après cette remarque, il paraît donc à propos d’étendre le nom de géométriques à tous les mouvements qui, sans l’être effectivement, le deviennent, en supprimant quelque machine ou partie de machine qui n’influe en rien sur l’état du système, et en regardant aussi comme parfaitement perméables l’un à l’autre les corps qui se touchent, sans qu’il s’exerce entre eux aucune pression, c’est-à-dire, sans qu’il y ait autre chose qu’une simple juxtaposition ; ainsi nous comprendrons dorénavant tous ces mouvements, sous le nom commun de mouvements géométriques, puisqu’en effet ils se déterminent également par des opérations purement géométriques » page 46

Mouvement géométrique

« (1) Il est évident que cette propriété appartient successivement aux mouvements que j’appelle ici géométrique, et que ce serait par conséquent en avoir une idée très fausse, que de les regarder comme des mouvements simplement possibles, c’est-à-dire, compatibles avec l’impénétrabilité de la matière : car, supposons, par exemple, que tout le système se réduise à deux globes adjacents, et se poussant l’un l’autre, il est clair que si l’on force ces corps à se séparer, ou à se mouvoir en sens contraire l’un de l’autre, ce mvt ne sera pas impossible, mais qu’en même temps les corps ne peuvent le prendre sans cesser d’agir l’un sur l’autre : ce mvt n’est donc pas propre à remplir le but qu’on se propose, qui est de ne rien changer à l’action réciproque des corps. » page 46

À cet endroit de l’article nous pouvons commencer à « éclaircir » l’influence de Carnot sur son fils. En effet, la question est de savoir si Sadi Carnot s’est inspiré de son père et comment il a trouvé les lois de la thermodynamique. Lazare Carnot a été très explicite en écrivant dans son essai, et d’ailleurs le nom de son essai le prouve, que son travail concerne toutes les machines en général. Il a inculqué à son fils cette « vision des choses » qui consiste à regarder au-delà des améliorations techniques. Sadi Carnot lui-même, dans son essai de 1824, s’intitulant « Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance », écrit clairement que « le phénomène de la production du mouvement par la chaleur n’a pas été considéré sous un point de vue général ». Aussi, son œuvre consistait à mettre en place « une théorie assez généralisée, pour faire connaître à l’avance tous les effets de la chaleur agissant d’une manière déterminée sur un corps quelconque ». Cela signifie qu’il fallait observer et étudier la chaleur. Mais, comment ?

Thermo

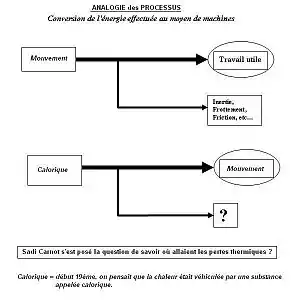
C’est ici que les réflexions de Lazare Carnot prennent leur importance. Pour le père, il ne peut y avoir de création de travail, dans une machine, sans pertes. Il estimait que « le mouvement que perd à chaque instant chacun des corps appliqués à cette machine, est en partie absorbé par la machine même, et en partie reçu par les autres corps du système ». C’est ce qu’il démontre dans son essai. Cette remarque va permettre a son fils de comprendre le fonctionnement des machines à feu.

La machine idéale que le jeune Sadi Carnot a imaginé dans son essai avec les quatre étapes thermodynamiques est utile pour comprendre et préciser le fonctionnement de la machine et les deux lois de la thermodynamique. Mais son rôle n’est pas d’innover.

L’appréhension de Carnot sur les forces résistantes est révélatrice de son hostilité envers le mouvement perpétuel qui est une illusion dont les méfaits sont quelquefois dévastateurs sur la société (industrielle ou autre). Effectivement pour Carnot il y a une antinomie entre le mouvement perpétuel et le fonctionnement même d’une machine. Le passage qui suit permettra au lecteur de relier entre eux les trois définitions de Carnot. On peut construire une machine selon les lois du mouvement géométrique mais c’est insuffisant pour augmenter la productivité de la machine. C’est une condition sine qua non.

Moment d'activité

« Parmi les forces appliquées à une machine en mouvement, les unes sont telles, que chacune d’entre elles fait un angle aigu avec la vitesse du point où elle est appliquée ;(…)» page 80 paragraphe 31

« (…), j’appellerai les premières forces mouvantes ou sollicitantes ; et les autres, forces résistantes (…) »

« On observera que les forces sollicitantes peuvent être dirigées dans le sens même de leurs vitesses, puisque alors l’angle formé par leurs concours est nul, et par conséquent aigu ; et que les forces résistantes peuvent agir dans le sens directement opposé à celui de leurs vitesses, (…) »

"(…)On voit par-là, que si on fait prendre un mouvement géométrique à un système quelconque de puissance, chacune d’elles sera sollicitante ou résistante à l’égard de ce mouvement géométrique, suivant que l’angle formé par cette force et sa vitesse géométrique, sera aigu ou obtus."

"Si une force P se meut avec la vitesse u, et que l’angle formé par le concours de u et P soit z, la quantité P cos(z) u dt dans laquelle dt exprime l’élément de temps, sera nommée moment d’activité, consommé par la force P pendant dt(...)" page 81 paragraphe 32

"Lorsqu’il s’agira d’un système de forces appliquées à une machine en mouvement,(…)"

« (..) le moment d’activité (total),…, est la même chose que la différence entre le moment d’activité consommé par les forces sollicitantes, et le moment d’activité, consommé en même temps par les forces résistantes, considéré comme une quantité positive. » page 82 paragraphe 32

Voyons comment Carnot répond à cette question fondamentale :

"Qu’est-ce qu’un corps ? C’est, disent la plupart, une étendue impénétrable, c’est-à-dire, qui ne peut en aucune manière être réduite à un espace moindre ; mais cette propriété n’est elle pas commune au corps et à l’espace vide ? Un pied cube de vide peut-il occuper un espace moindre ? Il est clair que non. Supposons qu’un pied cube d’eau, par exemple, soit enfermé dans un vase capable de contenir deux pieds cubes, et fermé de tous côtés ; qu’on agite, qu’on bouleverse ce vase tant qu’on voudra, il restera toujours un pied cube d’eau et un pied cube de vide : voilà deux espaces d’une nature différente, à la vérité, mais tout aussi irréductibles l’un que l’autre : ce n’est donc pas en cela que consiste la propriété caractéristique des corps."

Vase

"D’autres disent que cette propriété consiste dans la mobilité ; l’espace indéfini et vide, disent-ils, est immobile, tandis que les corps peuvent se transporter d’un lieu de cet espace à l’autre ; mais lorsque le corps A passe en B, par exemple, l’espace vide qui était en B n’a-t-il pas passé en A ? Il n’y a, ce me semble, pas plus de raison d’attribuer le mouvement au plein qui était en A, qu’au vide qui était en B, le mouvement consiste en ce que l’un de ces espaces a remplacé l’autre ; et ce remplacement étant réciproque, la mobilité est une propriété qui n’appartient pas plus à l’un qu’à l’autre. Sans sortir de notre première supposition, lorsque j’agite le vase moitié vide et moitié plein, le vide n’est-il pas mu tout aussi bien que le fluide ? Je plonge une boule de métal, creuse, dans une bouteille ; la boule va au fond ; ne voila-t-il pas un vide qui se meut dans un plein, tout de même que les corps se meuvent dans le vide ? L’espace plein ne diffère donc de l’espace vide, ni par la mobilité, ni par l’irréductibilité ; l’impénétrabilité qui distingue le premier du second, n’est donc pas la même chose que cette irréductibilité ; c’est un je ne sais quoi qu’on ne peut définir, parce que c’est une idée première."

"Les deux lois fondamentales dont je suis parti (XI)[1] sont donc des vérités purement expérimentales ; et je les ai proposées comme telles."

"Une explication détaillée de ces principes n’entrait pas dans le plan de cet ouvrage, et n’aurait peut-être servi qu’à embrouiller les choses : les sciences sont comme un beau fleuve, dont le cours est facile à suivre, lorsqu’il a acquis une certaine régularité ; mais si l’on veut remonter à la source, on ne la trouve nulle part, parce qu’elle est partout ; elle est répandue en quelque sorte sur toute la surface de la terre : de même si l’on veut remonter à l’origine des sciences, on ne trouve qu’obscurité, idées vagues, cercles vicieux ; et l’on se perd dans les idées primitives." (Terminus)