Torseur cinématique
Le torseur cinématique est un outil physique utilisé couramment en mécanique du solide.
Il permet de représenter de façon pratique le champ des vitesses d'un solide indéformable et donc de décrire les comportements de translation et de rotation d'un tel solide, en général dans un repère orthonormé direct. Comme son nom l'indique, il décrit la cinématique du solide indépendamment des causes du mouvement qui sont du ressort de la dynamique du solide. Il est important de ne pas le confondre avec le torseur cinétique, lequel est lié à la quantité de mouvement et au moment cinétique total du solide, c'est-à-dire des notions dynamiques.
Définition
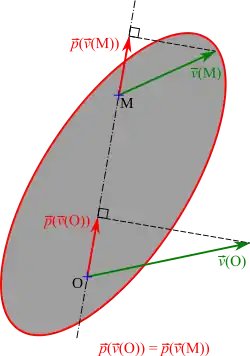
Soit un référentiel R, et un solide S. On peut définir en tout point M du solide le vecteur vitesse , dont la norme est exprimée en m s−1 ; il s'agit d'un champ vectoriel. Dans le cas d'un solide indéformable, on peut montrer que ce champ est équiprojectif (cf. l'article Modèle du solide indéformable » Champ des vitesses d'un solide).
Il s'agit donc d'un torseur, appelé torseur cinématique.
Physiquement, cette relation d'équiprojectivité est directement liée au fait que dans le modèle du solide indéformable la distance entre deux points quelconques du solide est constante : par suite on ne pourra pas définir le torseur cinématique pour un solide déformable.
Résultante et axe instantané de rotation
La résultante du torseur est appelée vecteur rotation, vecteur taux instantané de rotation, ou vecteur vitesse de rotation. Elle est notée . Sa norme s'exprime en rad s−1. C'est un pseudovecteur.
Ceci implique la relation suivante entre les vitesses de deux points B et A quelconques du solide :
- .

Physiquement, cette relation traduit le fait que, si Ω ≠ 0 (c'est-à-dire si le solide n'est pas en translation pure), alors il existe une droite (Δ) sur laquelle le vecteur vitesse est colinéaire à cette droite :
- .
Le solide est à un instant donné en rotation avec la vitesse angulaire Ω autour de cet axe (Δ) dont la direction est celle du vecteur .
Cet axe est appelé axe instantané de rotation. Dans le cas d'un mouvement plan, on définit ainsi le centre instantané de rotation.
On notera deux choses :
- Le vecteur vitesse de rotation représente un changement d'orientation du solide dans le référentiel. Il est nul dans le cas d'une translation, y compris une translation curviligne. Il peut donc être nul alors que le centre de gravité décrit un cercle, comme dans le cas de la translation circulaire ;
- La relation [1] permet de définir un vecteur vitesse (un moment) dans tout l'espace réel, y compris en des points en dehors de la pièce. On peut voir cette extrapolation de la manière suivante : la pièce a été taillée dans un gros bloc, et l'on détermine la vitesse qu'aurait eu le point du bloc primaire. Ceci est à la base de la notion de point coïncident ; en particulier, cela permet de déterminer la vitesse du centre du moyeu d'une liaison pivot.
Éléments de réduction
Comme tous les torseurs, le torseur cinématique peut être représenté par des éléments de réduction en un point, c'est-à-dire par la donnée de sa résultante et d'une valeur de son moment en un point A particulier. On note alors :
- .
Cela se lit : « le torseur V de S par rapport à R a pour élément de réduction oméga de S par rapport à R et V de A de S par rapport à R ».
Représentation en coordonnées cartésiennes
Le référentiel R est muni d'un repère orthonormé direct . Les vecteurs rotation et vitesse peuvent donc s'écrire en coordonnées cartésiennes :
- ;
- .
Le torseur peut alors se noter :
ou de façon équivalente :
Il est utile de préciser le repère dans lequel on exprime les composantes des vecteurs si l'on a besoin d'effectuer un changement de repère (voir ci-dessous la section #Torseur cinématique des liaisons parfaites).
Calcul des éléments de réduction en un autre point du solide
La règle du transport des moments, qui s'applique à tout torseur, permet de calculer les éléments de réduction du torseur en un point quelconque si on les connaît en un point donné :
Représentation d'un torseur cinématique
Pour tout point P du solide en mouvement, le vecteur vitesse est une combinaison de et du terme :
Loi de composition des mouvements
En relativité galiléenne, la loi de composition des mouvements s'exprime de manière simple :
- .
C'est une sorte de relation de Chasles pour les indices.
Chaîne cinématique et liaisons parfaites
L'utilisation des torseurs cinétiques est particulièrement intéressante lorsque l'on a une chaîne cinématique, c'est-à-dire un ensemble de pièces en contact les unes avec les autres. En effet, les torseurs cinématiques peuvent alors se simplifier : les contacts interdisent certains mouvements relatifs, et donc forcent à zéro certaines composantes des éléments de réduction du torseur en certains points particuliers.
Supposons que l'on a une chaîne formée de n pièces numérotées de 0 à n - 1 (0 étant habituellement le bâti de la machine ou bien le sol). Dans le cas d'une chaîne fermée, on peut écrire :
ce qui fournit une équation torsorielle, donc six équations scalaires pour un problème spatial, ou bien trois équations scalaires pour un problème plan. Par la loi de composition des mouvements, cette équation peut se développer :
Torseur cinématique des liaisons parfaites
Nous considérons les onze liaisons définies par la norme ISO 3952-1. Elles sont considérées comme parfaites, c'est-à-dire :
- sans adhérence : un mouvement relatif ne peut être bloqué que par obstacle ;
- avec un jeu minime (« sans jeu ») : il y a toujours contact entre les surfaces définies ;
- la position du mécanisme fait qu'aucune liaison n'est en butée.
Dans ces conditions, les éléments de réduction des torseurs des actions mécaniques transmissibles peuvent se simplifier, comme résumé dans le tableau ci-dessous.
Il convient de souligner que l'emplacement des zéros dépend de l'orientation de la liaison par rapport aux axes du repère. En particulier, il n'y a a priori aucune raison pour que les vecteurs caractéristiques de la liaison — normale de contact, ligne de contact — soient parallèles aux axes du repère général ; dans ces cas-là, il importe de préciser le repère local utilisé, puis d'effectuer un changement de repère pour pouvoir utiliser ce torseur avec les autres.
| Liaisons | Représentation | Éléments géométriques caractéristiques |
Mouvements relatifs possibles |
|---|---|---|---|
| Sphère plan
(ou Ponctuelle)* |
 |
point de contact A, normale |
|
| Linéaire-rectiligne* |  |
ligne de contact , normale |
|
| Sphère cylindre
(ou Linéaire-annulaire)* |
 |
centre de la sphère A, axe |
|
| Sphérique
(ou Rotule)* |
 |
centre de la sphère A | |
| Pivot-glissant |  |
axe du cylindre |
|
| Appui plan |  |
normale |
|
| Pivot |  |
axe du cylindre |
|
| Glissière |  |
direction | |
| Hélicoïdale |  |
axe de l'hélice , | |
| Sphérique
(ou Rotule à doigt)* |
 |
centre de la sphère A, rotation bloquée selon |
|
| Encastrement | aucun |
* Ancienne normalisation NF E 04-015
Exemple de mise en œuvre du torseur des actions mécaniques transmissibles
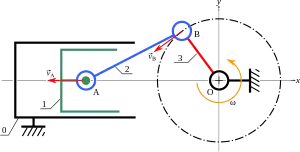
Considérons un système composé d'un piston (noté 1), d'une bielle (notée 2) et d'un vilebrequin (noté 3), le bâti étant noté 0. La longueur OB de manivelle vaut 30 mm, la longueur AB de la bielle vaut 80 mm. Le système tourne avec une fréquence N = 3 000 tr/min.
Quelle est la vitesse du piston V(A∈1/0) lorsque le vilebrequin fait un angle (x, OB) = 150° ?
Les coordonnées des points sont (en mètre) :
- .
La loi de composition des mouvements s'écrit :
- .
- Il est à noter que l'on peut aussi considérer la chaîne cinématique fermée 0 → 1 → 2 → 3 → 0, ce qui nous donne l'équation équivalente :
- .
Toutes les composantes sont exprimées dans le repère ; on omettra donc d'indiquer le repère afin d'alléger la notation. D'après la nature des liaisons, on a :
- liaison 1/0 pivot-glissant d'axe Ax : ;
- liaison 1/2 pivot-glissant d'axe Az : ;
- liaison 2/3 pivot d'axe Bz : ;
- liaison 3/0 pivot d'axe Oz :
avec ωz(3/0) = π × N/30 = 314 rad s−1.
On applique la simplification des problèmes plans :
On vérifie que l'on n'a pas plus de trois inconnues.
Pour minimiser le nombre de calculs, on transporte les torseurs là où il y a plus d'inconnues, c'est-à-dire en A :
- .
Soit :
La loi de composition des mouvements nous donne :
- .
D'où :
- .
On a donc :
- .
Et enfin :
- .
On remarquera au passage que la troisième équation (l'équation des vitesses de rotation) était inutile.
Notes et références
Bibliographie
- Michel Combarnous, Didier Desjardins et Christophe Bacon, Mécanique des solides et des systèmes de solides, Dunod, coll. « Sciences sup », , 3e éd. (ISBN 978-2-10-048501-7)
- José-Philippe Pérez, Cours de Physique : mécanique : Fondements et applications, Masson, coll. « Masson Sciences », , 6e éd., 748 p. (ISBN 978-2-10-005464-0)
- Jean-Louis Fanchon, Guide de mécanique, Nathan, , 543 p. (ISBN 978-2-09-178965-1), p. 190-194