Théorie de la décision dans l'incertain

Un décideur peut choisir d'assurer sa voiture contre le vol pour un an (décision ${\displaystyle d_{1}}$) ou pas (décision ${\displaystyle d_{2}}$). Au cours de cette année il peut soit se faire voler sa voiture (événement ${\displaystyle e_{1}}$) soit pas (événement ${\displaystyle e_{2}}$). De plus nous savons que la voiture a une valeur de 100 000 € et que l'assurance contre le vol coûte 5 000 €. Dans cet exemple le décideur est soumis au choix entre deux loteries, la loterie ${\displaystyle L_{1}=(-5000,e_{1};-5000,e_{2})}$ qui découle de la décision ${\displaystyle d_{1}}$ et la loterie ${\displaystyle L_{2}=(-100000,e_{1};0,e_{2})}$ qui découle de la décision ${\displaystyle d_{2}}$. Le tableau ci-dessous illustre la situation de choix soumis au décideur. Si le décideur choisit de s'assurer alors ${\displaystyle V(L_{1})>V(L_{2})\Rightarrow L_{1}\succ L_{2}}$.

Exemple 1

	${\displaystyle e_{1}}$	${\displaystyle e_{2}}$
${\displaystyle d_{1}}$	-5 000 €	-5000€
${\displaystyle d_{2}}$	-100 000 €	0 €

Au XVII^e siècle, au moment où se développe la théorie moderne des probabilités, des mathématiciens comme Pascal et De Fermat font l'hypothèse que l'évaluation d'une loterie ${\displaystyle L}$ se fait via un calcul de son espérance de gain :

${\displaystyle E(L)=\sum _{i=1}^{n}p_{i}\times x_{i}}$

Cependant, il est intéressant de remarquer qu'un décideur qui prend ses décisions en fonction de l'espérance de gain peut parfois prendre des décisions étonnantes, comme le montre le paradoxe de Saint-Pétersbourg proposé initialement par Nicholas Bernoulli dans une lettre en 1713. Ce paradoxe a ensuite été repris et modifié par Daniel Bernoulli, son neveu, et a été discuté dans les Transactions de l'Académie de Saint-Pétersbourg, d'où son nom. Le principe du jeu de Saint-Pétersbourg est le suivant : on lance en l'air une pièce de monnaie. Si Face apparaît, la banque paie 2 € au joueur, et on arrête le jeu. Sinon, on relance la pièce. Si Face apparaît, la banque paie 4 € au joueur, et on arrête le jeu. Sinon, on relance la pièce. Si Face apparaît, la banque paie 8 € au joueur, et ainsi de suite. Autrement dit, si Face apparaît pour la première fois au ${\displaystyle n}$-ième lancer, la banque paie ${\displaystyle 2^{n}}$€ au joueur.

On propose maintenant au décideur de déterminer la somme qu'il serait prêt à miser pour jouer à ce jeu. Le décideur détermine alors la mise pour laquelle le jeu est équitable (au sens de l'espérance de gain), c'est-à-dire la mise maximale qu'il peut mettre en jeu pour que l'espérance de gain reste positive. Dans ce jeu pour gagner ${\displaystyle 2^{n}}$ il faut faire ${\displaystyle n-1}$ fois Pile avant de faire Face, la probabilité de gagner ${\displaystyle 2^{n}}$€ est donc de ${\displaystyle 1/2^{n}}$. Ainsi l'espérance de gain de ce jeu, sans prendre en compte la mise, est de :

${\displaystyle \sum _{i=1}^{+\infty }{\frac {1}{2^{i}}}\times 2^{i}=\sum _{i=1}^{+\infty }1}$.

On en conclu qu'un décideur qui se fie à l'espérance de gain pour prendre ses décisions sera prêt à payer n'importe quelle mise pour pouvoir jouer à ce jeu, puisque son espérance de gain restera infinie quelle que soit sa mise de départ. Pourtant aucun décideur raisonnable ne serait prêt à miser plus de quelques euros pour jouer à ce jeu.

Daniel Bernoulli résout ce paradoxe en introduisant l'hypothèse selon laquelle les individus ne maximisent pas l'espérance de gain mais une espérance morale :

${\displaystyle E(L)=\sum _{i=1}^{n}p_{i}\times u(x_{i})}$

où ${\displaystyle u}$ est une fonction logarithmique. Pour Bernoulli, la valeur subjective d'un jeu n'augmente pas linéairement avec la valeur monétaire de la récompense, mais avec un taux décroissant. Sous une telle hypothèse de la non-linéarité du traitement des conséquences d'une loterie par le décideur, le paradoxe de Saint-Pétersbourg est complètement résolu. La fonction ${\displaystyle u}$ est appelée fonction d'utilité. Ce sont ces travaux qui ont inspiré la théorie de l'utilité espérée proposée par John von Neumann et Oskar Morgenstern.

La théorie de l'utilité espérée (aussi appelée théorie EU, de l'anglais « expected utility ») est une théorie de la décision en environnement risqué développée par John von Neumann et Oskar Morgenstern dans leur ouvrage Theory of Games and Economic Behavior (1944). Dans l'optique de fournir une théorie solide sur la modélisation des préférences d'un décideur en situation risquée, von Neuman et Morgenstern généralisent le modèle de Bernoulli fondé sur l'usage d'une fonction d'utilité. Ils montrent, après avoir définit un ensemble d'axiomes sur les préférences d'un décideur, qu'il est toujours possible de construire une fonction d'utilité sur les conséquences d'une loterie, de manière à ce que l'espérance de ces utilités sur les loteries conserve l'ordre de préférence entre les loteries du décideur. La fonction d'utilité construire est alors unique à une transformation affine croissante près. En d'autres termes, si la fonction ${\displaystyle u}$ modélise les préférences du décideur, alors il en est de même pour la fonction ${\displaystyle v}$ si et seulement si ${\displaystyle v(x)=a\times u(x)+b}$ avec ${\displaystyle a}$ un réel strictement positif et ${\displaystyle b}$ un réel quelconque. Le modèle de l'espérance d'utilité, sous de tels hypothèses revient alors à calculer l'espérance d'utilité de la loterie :

${\displaystyle EU(L)=\sum _{i=1}^{n}p_{i}\times u(x_{i})}$

où ${\displaystyle u}$ est la fonction d'utilité construite via la théorie de l'utilité espérée. En 1953, Maurice Allais propose un paradoxe remettant en cause la capacité à décrire les comportements des décideurs, en illustrant la non validité de l'axiome d'indépendance posé par von Neumann et Morgenstern.

Le contenu descriptif du modèle de décision EU a été rapidement critiqué dans une expérience restée célèbre sous le nom de « paradoxe d'Allais ». La version présentée ici est celle de Kahneman et Tversky. Les sujets doivent choisir entre deux paires de loteries. D'une part, entre ${\displaystyle L_{1}=(3000,1)}$ et ${\displaystyle L_{1}'=(0,0.1;4000,0.9)}$ et, d'autre part, entre ${\displaystyle L_{2}=(0,0.9;3000,0.1)}$ et ${\displaystyle L_{2}'=(0,0.91;4000,0.09)}$. Dans la première situation de choix, la grande majorité des décideurs soumises à cette expérience préfèrent la loterie ${\displaystyle L_{1}}$à la loterie ${\displaystyle L_{1}'}$(ils préfèrent être surs de gagner 3 000 € que de risque de ne rien gagner, un tien vaut mieux que deux tu l'auras). Dans la seconde situation de choix, la majorité des décideurs préfèrent la loterie ${\displaystyle L_{2}'}$ à la loterie ${\displaystyle L_{2}}$(car la probabilité de gagner 4 000 € dans la loterie ${\displaystyle L_{2}'}$ et presque la même que celle de gagner 3 000 € dans la loterie ${\displaystyle L_{2}}$). Si on traduit ce préférences dans le cadre du modèle EU, on obtient alors :

${\displaystyle {\begin{aligned}L_{1}\succ L_{1}'&\Leftrightarrow &EU(L_{1})>EU(L_{1}')\\&\Leftrightarrow &u(3000)>0.1\times u(0)+0.9\times u(4000)\\&\Leftrightarrow &0.1\times u(3000)>0.01\times u(0)+0.09\times u(4000)\\&\Leftrightarrow &0.1\times u(3000)+0.9\times u(0)>0.01\times u(0)+0.09\times u(4000)+0.9\times u(0)\\&\Leftrightarrow &0.1\times u(3000)+0.9\times u(0)>0.91\times u(0)+0.09\times u(4000)\\&\Leftrightarrow &L_{2}\succ L_{2}'\end{aligned}}}$

Ainsi, quelle que soit la fonction d'utilité utilisée, la préférence pour ${\displaystyle L_{1}}$sur ${\displaystyle L_{1}'}$ est équivalente à la préférence pour ${\displaystyle L_{2}}$ sur ${\displaystyle L_{2}'}$. Ce qui est incompatible avec les résultats de l'expérience menée par Maurice Allais. Allais qualifie ce comportement, loin d'être paradoxal, comme un comportement raisonnable de préférence for security in the neighbourhood of certainty. Ce phénomène est connu sous le nom de l'effet de certitude. Ce phénomène est aujourd'hui bien connu sous le nom de l'effet de certitude . Le renversement de préférences s'explique ici simplement par l'attraction forte du passage de la quasi-certitude à la certitude, et à l'indifférence du passage du peu probable au un peu plus probable. À cela s'ajoute un phénomène de sur-pondération des résultats qui sont certains par rapport aux résultats qui ne sont que probables.[12]

De nombreux autres exemples et critiques ont été formulés dans la littérature économique à l'encontre du modèle EU et la plupart s'accordent à dire que l'axiome d'indépendance est une hypothèse bien trop forte comme le montre le paradoxe d'Allais. Gayant qualifie même de paradoxal le fait de modéliser l'aversion au risque d'un décideur en se fondant sur une fonction portant uniquement sur les conséquences (sans la prise en compte d'éléments probabilistes). Au début du millénaire, Rabin énonce son théorème d'impossibilité sur le critère EU : l'impossibilité de traduire une aversion pour le risque lorsque les enjeux sont faibles dans le cadre du modèle EU[13]. En effet, la concavité de la fonction d'utilité permet d'expliquer l'aversion au risque lorsque les enjeux sont très importants mais implique également une quasi-neutralité vis-à-vis du risque lorsque les enjeux sont plus faibles[14]. En plus de rendre abusivement élevée l'aversion pour le risque lorsque les enjeux sont importants, de nombreuses expériences ont montré l'existence d'une aversion au risque sur les petits enjeux. L'existence d'une aversion pour les petits enjeux met alors en échec la

capacité du modèle EU à décrire l'aversion pour le risque. La solution suggérée pour sortir de ce théorème d'impossibilité est de décharger la fonction d'utilité pour qu'elle ne décrive plus l'aversion au risque mais se contente uniquement de son rôle premier de traduire le degré d'importance d'une conséquence pour le décideur. C'est ce que se propose de faire les modèles dit non-EU.

Dans la multitude de propositions de modèles non-EU qu'aura connu le XX^e siècle, certains ont marqué la communauté scientifique. C'est notamment le cas du modèle de l'utilité espérée généralisée proposé par Machina[15]. Ce dernier part du principe que le respect de l'axiome d'indépendance n'est pas une condition nécessaire pour préserver l'hypothèse de maximisation de l'utilité espérée. Ainsi, ce modèle rejette totalement l'axiome d'indépendance et pose des conditions analytiques sur les préférences. Si ce modèle résout quelques situations qui mettaient dans l'impasse le modèle EU, il reste encore trop proche du modèle EU et de légères modifications des paradoxes classiques (comme le paradoxe d'Allais) les font redevenir insolubles.

D'autres propositions de modèles se sont focalisées sur un affaiblissement de l'axiome d'indépendance. Ces modèles dits de betweenness restent néanmoins dans l'impasse dans des situations similaires au paradoxe d'Allais.

Enfin une autre famille de modèles reposant sur une restriction de l'axiome d'indépendance ont permis d'établir des modèles ayant un fort pouvoir descriptif des décideurs et pouvant résoudre n'importe quel paradoxe connu. Ces modèles sont dits à dépendance des rangs. Le plus connu et le plus utilisé étant celui de l'utilité espérée dépendant du rang (Rank Dependent Utility, RDU) proposé par Quiggin[16].

Le tableau ci-dessous propose une synthèse des principaux modèles non-EU dans la littérature.

Buffon a proposé une seconde façon de résoudre le paradoxe de Saint-Pétersbourg, par l'introduction de l'hypothèse que les décideurs négligent les petites probabilités et considèrent comme impossible une succession de plus de ${\displaystyle n}$ Piles à la suite. Le décideur se refuse alors à payer une mise supérieure à ${\displaystyle 2^{n}}$€. C'est justement cette idée qui a inspiré les modèles à transformation des probabilités. Cette idée de traiter non linéairement les probabilités est la vision duale du traitement non linéaire des conséquences. Handa propose une solution qui ajoute au modèle EU une fonction croissante ${\displaystyle \varphi$ :[0;1]\rightarrow [0;1]} telle que ${\displaystyle \varphi (0)=0}$ et ${\displaystyle \varphi (1)=1}$ qui permet de déformer les probabilités en accord avec les préférences du décideur[24]. En d'autre terme l'évaluation d'une loterie par ce critère vaut:

${\displaystyle V(L)=\sum _{i=1}^{n}\varphi (p_{i})u(x_{i})}$)

Si l'idée semble séduisante, elle est rapidement abandonnée, car ce modèle peut conduire à prendre des choix non rationnels[18].

En théorie de la décision dans le risque, on considère que la préférence de la loterie ${\displaystyle L_{1}}$ et ${\displaystyle L_{2}}$ est rationnelle si ${\displaystyle non(L_{1}\succ _{FSD}L_{2})}$ où ${\displaystyle \succ _{FSD}}$ est la dominance stochastique du premier ordre définie par:

${\displaystyle L_{1}\succ _{FSD}L_{2}}$ si et seulement si ${\displaystyle \forall x\in X,G_{L_{1}}(x)\geq G_{L_{2}}(x)}$ et ${\displaystyle \exists x\in X,G_{L_{1}}(x)>G_{L_{2}}(x)}$ où ${\displaystyle G_{L}(x)=\sum _{1\leq i\leq n~tq~x_{i}\geq x}p_{i}}$ représente la fonction décumulative de la loterie ${\displaystyle L}$.

Représentation graphique du modèle RDU par Gayant

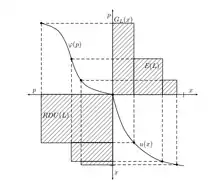
L'idée de déformer les probabilités aurait pu sombrer dans l'oubli si Quiggin n'avait pas eu l'idée clef de transformer non pas des probabilités mais des cumuls de probabilités afin d'écarter toute violation de la dominance stochastique du premier ordre par le décideur. La seconde idée clef de ce modèle repose sur l'hypothèse de dépendance du rang : le poids attribué à une conséquence ne dépend pas uniquement de la probabilité d'obtenir cette conséquence, mais également de l'attractivité du rang du rang de cette dernière par rapport aux autres conséquences possibles. Le modèle RDU propose d'évaluer une loterie ${\displaystyle L=(x_{1},p_{1};...;x_{n},p_{n})}$ telle que ${\displaystyle x_{1}<...<x_{n}}$ comme suit:

${\displaystyle RDU(L)=u(x_{1})+\sum _{i=2}^{n}\varphi (G_{L}(x))\times (u(x_{i})-u(x_{i-1}))}$

Le pouvoir descriptif du modèle RDU et sa capacité à conserver une rationalité de choix en fait un des modèles les plus utilisés en représentation des préférences d'un décideur dans le risque.

Au début des années 1930, Ramsey et de Finetti suggèrent qu'en cas d'absence de distribution de probabilité objective, les décideurs établissent eux-mêmes ces probabilités de manière subjective. Ces probabilités doivent rester positives, additives et l'événement certain doit avoir une probabilité de 1 de se réaliser. Le modèle le plus simple est le modèle de l'espérance subjective (Subjective Expected, SE)[25] proposé par Savage.

L'hypothèse faite ici, est que le décideur établit une distribution ${\displaystyle Q}$ de probabilité subjective sur les états de la nature et procède à un calcul d'espérance de gain pour évaluer la loterie. En d'autres terme l'évaluation de la loterie ${\displaystyle L=(x_{1},e_{1};...;x_{n},e_{n})}$ vaut :

${\displaystyle SE(L)=\sum _{i=1}^{n}Q(e_{i})\times x_{i}}$

À l'instar de l'espérance de gain dans le cadre du risque, ce modèle tombe sous le coup du paradoxe de Saint-Pétersbourg. Pour pallier cela, à la suite de la proposition du modèle EU par von Neumann et Morgenstern, Savage propose la généralisation du modèle SE en assignant une fonction d'utilité ${\displaystyle u}$ au décideur et postule que les décideurs évaluent une loterie comme suit:

${\displaystyle SEU(L)=\sum _{i=1}^{n}Q(e_{i})\times u(x_{i})}$

Ce modèle est connu sous le nom de l'espérance subjective d'utilité (Subjective Expected Utility, SEU). De façon semblable au modèle EU dans le risque, ce modèle repose sur un axiome qui impose un traitement linéaire des probabilités : le principe de la chose sure, qui est le pendant de l'axiome d'indépendance dans le cadre du risque. Malgré l'attrait sur le plan normatif du modèle SEU, Daniel Ellsberg publie les résultats d'une expérience qui met en évidence l'incapacité du modèle SEU à modéliser les comportements dans l'incertain. Cette expérience est connue sous le nom de paradoxe d'Ellsberg.

On place dans une urne opaque 30 boules bleues et 60 boules vertes ou rouges (dans des proportions inconnues). Le nombre de boules vertes réelles est donc inconnu, de même que le nombre de boules rouges. On tire au hasard une boule dans cette urne (on fait l'hypothèse que chaque boule a autant de chance qu'une autre d’être tirée). On propose dans un premier temps, de choisir entre deux jeux:

• Jeu 1 : Si la boule tirée est de couleur bleue, alors vous gagnez 100 €.
• Jeu 2 : Si la boule tirée est de couleur verte, alors vous gagnez 100 €.

Ce qui correspond à choisir entre la loterie ${\displaystyle L_{1}=(100,bleue;0,rouge;0,verte)}$ et la loterie ${\displaystyle L_{2}=(0,bleue;0,rouge;100,verte)}$

Dans un second temps, on propose au joueur de choisir entre deux autres jeux :

• Jeu 3 : Si la boule tirée est de couleur bleue ou rouge, alors vous gagnez 100 €.
• Jeu 4 : Si la boule tirée est de couleur verte ou rouge, alors vous gagnez 100 €.

Ce qui correspond à choisir entre la loterie ${\displaystyle L_{3}=(100,bleue;100,rouge;0,verte)}$ et la loterie ${\displaystyle L_{4}=(0,bleue;100,rouge;100,verte)}$.

Les résultats de l'expérience d'Ellsberg ont montré que la majorité des personnes qui se sont pliées à cette expérience ont préféré le jeu 1 au jeu 2 (i.e., ${\displaystyle L_{1}\succ L_{2}}$) et en même temps ont préféré le jeu 4 au jeu 3 (i.e., ${\displaystyle L_{4}\succ L_{3}}$). Ces préférences sont en contradictions avec les prescriptions du modèle SEU. En effet, si on note ${\displaystyle e_{B}}$ l'événement "la boule tirée est bleue", ${\displaystyle e_{V}}$ l'événement "la boule tirée est verte" et ${\displaystyle e_{R}}$ l'événement "la boule tirée est rouge", alors les préférences du décideur pour le premier choix s'écrivent :

${\displaystyle {\begin{aligned}L_{1}\succ L_{2}&\Leftrightarrow &SEU(L_{1})>SEU(L_{2})\\&\Leftrightarrow &Q(e_{V}\cup e_{R})\times u(0)+Q(e_{B})\times u(100)>Q(e_{B}\cup e_{R})\times u(0)+Q(e_{V})\times u(100)\\&\Leftrightarrow &Q(e_{B})>Q(e_{V})\\\end{aligned}}}$

car la fonction ${\displaystyle u}$ est unique à une transformation affine près (on peut donc supposer que ${\displaystyle u(0)=0}$ sans perte de généralité). De la même manière, les préférences du décideur pour le second choix s'écrivent :

${\displaystyle {\begin{aligned}L_{4}\succ L_{3}&\Leftrightarrow &SEU(L_{4})>SEU(L_{3})\\&\Leftrightarrow &Q(e_{B})\times u(0)+Q(e_{V}\cup e_{R})\times u(100)>Q(e_{V})\times u(0)+Q(e_{B}\cup e_{R})\times u(100)\times u(100)\\&\Leftrightarrow &Q(e_{V}\cup e_{R})>Q(e_{B}\cup e_{R})\\&\Leftrightarrow &Q(e_{V})+Q(e_{R})>Q(e_{B})+Q(e_{R})\\&\Leftrightarrow &Q(e_{V})>Q(e_{B})\\\end{aligned}}}$

car la distribution de probabilité ${\displaystyle Q}$ est additive (i.e., ${\displaystyle Q(e_{B}\cup e_{R})=Q(e_{B})+Q(e_{R})}$ et ${\displaystyle Q(e_{V}\cup e_{R})=Q(e_{V})+Q(e_{R})}$).

Les deux inégalités obtenus sont contradictoires, ce qui rend non modélisables par le modèle SEU les préférences des décideurs soumis à cette expérience.

Le renversement des préférences s'explique ici simplement. Dans les deux choix, on propose au décideur de choisir entre un jeu où les probabilités sont parfaitement définies et un jeu où l'on ne connaît pas les probabilités de manière certaine. Cette expérience met en avant le faire que les décideurs préférent généralement les situations où les probabilités sont parfaitement définies aux situations où les probabilités sont mal connues. Ce trait comportemental est nommé l'aversion à l'ambiguïté.

Afin de résoudre ce paradoxe, il est nécessaire d'établir un modèle qui autorise en même temps la propriété ${\displaystyle Q(e_{B})>Q(e_{V})}$ et la propriété ${\displaystyle Q(e_{B}\cup e_{R})<Q(e_{V}\cup e_{R})}$. Ce qui est possible dès lors que l'on autorise une propriété de non additivité à la distribution ${\displaystyle Q}$. La problématique rencontrée ici est très similaire à la problématique rencontrée dans le cadre du risque et la solution également très similaire. Schmeidler postule qu'il ne faut pas établir les probabilités subjectives en les définissant uniquement sur les événements simples mais les définir également sur les unions des événements simples. Ce modèle est connu sous le nom de l'espérance d'utilité à la Choquet (Choquet Expected Utility, CEU) et permet de résoudre le paradoxe d'Ellsberg[27].

Il est commode de représenter de manière graphique un problème de décision séquentielle dans l'incertain. Un modèle graphique très utilisée dans la littérature est celui des arbres de décision[28]^,[29], qui permettent une représentation simple et explicite du problème.

Un graphe orienté ${\displaystyle G=({\mathcal {N}},{\mathcal {E}})}$ est composé d'un ensemble fini ${\displaystyle {\mathcal {N}}}$de nœuds et d'un ensemble fini ${\displaystyle {\mathcal {E}}}$ d'arcs. Un arc est un couple de nœuds ${\displaystyle (N_{1},N_{2})}$ tel que ${\displaystyle \{N_{1},N_{2}\}\subseteq {\mathcal {N}}}$. Si ${\displaystyle (N_{1},N_{2})\in {\mathcal {E}}}$, on dit alors que le nœud ${\displaystyle N_{1}}$ est le père du nœud ${\displaystyle N_{2}}$ et que le nœud ${\displaystyle N_{2}}$ est le fils du nœud ${\displaystyle N_{1}}$.

Un chemin allant du nœud ${\displaystyle N}$ au nœud ${\displaystyle N'}$ est un ensemble d'arcs ${\displaystyle {\mathcal {E}}'=\{(N_{1},N_{2}),...,(N_{n-1},N_{n})\}\subseteq {\mathcal {E}}}$ où ${\displaystyle N_{1}=N}$ et ${\displaystyle N_{n}=N'}$. La longueur du chemin est donnée par le nombre d'arcs de ${\displaystyle {\mathcal {E}}'}$.

Le sous-graphe ${\displaystyle G'}$ de ${\displaystyle G}$, induit par l'ensemble de nœuds ${\displaystyle {\mathcal {N}}'\subseteq {\mathcal {N}}}$, est le graphe ${\displaystyle G'=({\mathcal {N}}',{\mathcal {E}}')}$ où ${\displaystyle {\mathcal {E}}'=\{(N,N'):\{N,N'\}\subseteq {\mathcal {N}},(N,N')\in {\mathcal {E}}\}}$.

Un arbre ${\displaystyle T=({\mathcal {N}},{\mathcal {E}})}$ est un graphe orienté dans lequel il existe exactement un nœud, que l'on appelle racine, à partir duquel il existe exactement un chemin allant à chaque nœud. Dans un arbre, s'il existe un chemin allant de ${\displaystyle N}$ à ${\displaystyle N'}$, on dit que le nœud ${\displaystyle N}$ est un ancêtre du nœud ${\displaystyle N'}$ et on dit que ${\displaystyle N'}$ est un descendant du nœud ${\displaystyle N}$. Enfin on note ${\displaystyle N_{r}}$ la racine d'un arbre. On appelle profondeur ou hauteur d'un arbre la longueur du chemin le plus long depuis la racine vers une feuille.

Le sous-arbre ${\displaystyle T(N)}$ de ${\displaystyle T}$, est l'arbre de racine ${\displaystyle N\subseteq {\mathcal {N}}}$ qui est le sous-graphe de l'arbre ${\displaystyle T}$ induit par le nœud ${\displaystyle N}$ et les descendants de ${\displaystyle N}$ dans l'arbre ${\displaystyle T}$.

Un arbre de décision ${\displaystyle T}$ est un arbre dont l'ensemble des nœuds ${\displaystyle {\mathcal {N}}}$ est partitionné en trois sous-ensembles disjoints :

• ${\displaystyle {\mathcal {N}}_{D}}$ : l'ensemble des nœuds de décision, que l'on représente graphiquement pas des rectangles. Ils représentent les états où le décideur est amené à prendre une décision. Les arcs issus d'un nœud de décision représentent les décisions que peur prendre le décideur en ce nœud.
• ${\displaystyle {\mathcal {N}}_{C}}$ : l'ensemble des nœuds de chance, que l'on représente graphiquement par des cercles. Ils représentent les états où la nature intervient (autrement dit, les incertitudes du problème). Les arcs issus d'un nœud de chance représentent les différents événement qui peuvent se réaliser à l’issue de ce nœud.
• ${\displaystyle {\mathcal {C}}}$ : l'ensemble des nœuds terminaux (ou conséquences), qui sont les feuilles de l'arbre (i.e., nœuds n'ayant pas de fils). ils représentent les états terminaux d'un problème de décision séquentielle. Une valeur d'utilité ${\displaystyle u(N)}$ est associée à chaque nœud ${\displaystyle N}$, correspondant à l'utilité de la conséquence représentée par le nœud ${\displaystyle N}$.
  

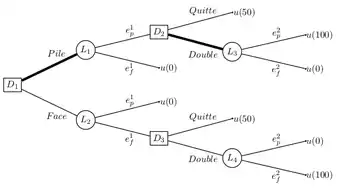  Arbre de décision représentant un problème de décision séquentielle dans l'incertain. La stratégie {(D1, L1), (D2, L3)} est représentée en gras.

Sans perte de généralité on impose que la racine de l'arbre est toujours un nœud de décision. Une stratégie pour un arbre de décision ${\displaystyle T=({\mathcal {N}},{\mathcal {E}})}$ est un ensemble d'arcs ${\displaystyle \Delta =\{(N,N'):N\in {\mathcal {N}}_{D}^{\Delta },N'\in {\mathcal {N}}^{\Delta }\}\subseteq {\mathcal {E}}}$ où ${\displaystyle {\mathcal {N}}_{D}^{\Delta }={\mathcal {N}}_{D}\cap {\mathcal {N}}^{\Delta }}$ et ${\displaystyle {\mathcal {N}}^{\Delta }\subseteq {\mathcal {N}}}$ est un ensemble de nœuds qui contient:

• la racine
• un fils exactement pour chaque nœud ${\displaystyle N\in {\mathcal {N}}_{D}^{\Delta }}$
• tous les fils pour chaque nœud ${\displaystyle N\in {\mathcal {N}}_{C}^{\Delta }={\mathcal {N}}_{C}\cap {\mathcal {N}}^{\Delta }}$

La restriction d'une stratégie à un sous-arbre, qui est une stratégie dans ce sous-arbre, est appelée une sous-stratégie.

Généralement, un tel arbre est représenté horizontalement de manière à ce que les différents nœuds suivent l'ordre chronologique depuis la gauche vers la droite. Notons également que, dans la pratique, on omet de préciser l'orientation des arcs lorsque l'on représente graphiquement un arbre de décision, l'orientation se déduisant naturellement à partir de l'ordre chronologique.

Un décideur soumis à un problème de décision séquentielle dans l'incertain est alors amené à choisir entre différentes stratégies. Pour ce faire, la théorie de la décision se propose de réduire les stratégies à des loteries. Pour cela elle fait l'hypothèse de l'axiome de réduction des loteries composées (ou encore appelé axiome de neutralité).

L'axiome de réduction des loteries composées suppose commes équivalentes ces deux loteries.

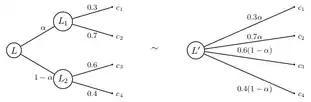
Soit ${\displaystyle X=\{x_{1},x_{2},...,x_{n}\}}$ un ensemble de conséquences non vide, et ${\displaystyle P}$ une loi de probabilité sur ${\displaystyle X}$ telle que ${\displaystyle P(X)=1}$. L'ensemble des loteries ${\displaystyle \mathbb {L} _{X}}$ à support dans ${\displaystyle X}$ est un ensemble convexe. C'est-à-dire que :

${\displaystyle \forall \alpha \in [0,1],\forall (L_{1},L_{2})\in \mathbb {L} _{X}^{2},\alpha L_{1}+(1-\alpha )L_{2}\in \mathbb {L} _{X}}$

Cette propriété de mixage peut être vue comme un composition de loterie[30]. La loterie ${\displaystyle \alpha L_{1}+(1-\alpha )L_{2}}$ correspond à la loterie à deux étapes qui, dans un premier temps, offre les loteries ${\displaystyle L_{1}}$ et ${\displaystyle L_{2}}$ avec les probabilités ${\displaystyle \alpha }$ et ${\displaystyle 1-\alpha }$ respectivement et, à la seconde étape, offre la conséquence ${\displaystyle x\in X}$. Cet axiome considère comme équivalent la loterie composée (à plusieurs étape) et sa forme réduite (à une étape).

Réduction d'une stratégie en loterie

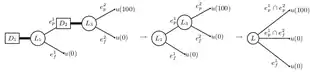
À partir d'une stratégie ${\displaystyle \Delta }$ on peut élaguer tous les sous-arbres descendants des arcs issus des nœuds de décision n'appartenant pas à la stratégie ${\displaystyle \Delta }$. L'arbre obtenu ne contient que des nœuds de décision ayant un unique fils. Ces derniers peuvent être supprimés en rattachant ce fils à leur père. Les nœuds restants forment une loterie composée. La loterie composée obtenue peut être réduite via la RLC. La loterie résultante peut enfin s'évaluer avec n'importe quel critère issu de la théorie de la décision dans l'incertain.

Un critère de décision s'applique dans la littérature indifféremment sur une loterie ou sur une stratégie dès lors que la RLC est supposée. Un décideur préfère la stratégie ${\displaystyle \Delta _{1}}$ à la stratégie ${\displaystyle \Delta _{2}}$ au sens du critère de décision ${\displaystyle V}$ si et seulement si ${\displaystyle V(\Delta _{1})>V(\Delta _{2})}$.

Le nombre de stratégie possibles dans un arbre de décision peut être de taille exponentielle en la t'aille de l'arbre[31]. Face à ce constat il n'est pas envisageable d'énumérer l'ensemble des stratégies pour les évaluer une à une afin de sélectionner celle maximisant le critère de décision donné. La recherche d'une stratégie optimale, au sens d'un critère de décision donné, est un problème algorithmique qui peut s'avérer compliqué.

Dans le cadre du modèle EU, la recherche de la stratégie optimale peut s'obtenir par un algorithme de programmation dynamique, dont le principe est de construire la stratégie optimale en remontant, par induction arrière dans l'arbre de décision, la meilleure stratégie de chaque sous-arbre. L'algorithme permettant de remonter la stratégie optimale et sa valeur au sens du modèle EU est le suivant :

ProgDyn(nœud ${\displaystyle N}$):

 si ${\displaystyle N\in {\mathcal {C}}}$ alors:
  retouner (${\displaystyle \emptyset ,u(N)}$)

 si ${\displaystyle N\in {\mathcal {N}}_{D}}$ alors:
   s_opt, v_max := (${\displaystyle \emptyset }$, ${\displaystyle -\infty }$)
   pour chaque nœud ${\displaystyle N'}$ fils de ${\displaystyle N}$:
     s_tmp, v_tmp := ProgDyn(${\displaystyle N'}$)
     si v_tmp > v_max alors:
       s_opt, v_max := ${\displaystyle \{(N,N')\}~\cup }$ s_tmp, v_tmp
   retourner (s_opt, v_max)

 si ${\displaystyle N\in {\mathcal {N}}_{C}}$ alors:
   s_opt, v_max := (${\displaystyle \emptyset }$, 0)
   pour chaque nœud ${\displaystyle N'}$ fils de ${\displaystyle N}$:
     s_tmp, v_tmp := ProgDyn(${\displaystyle N'}$)
     s_opt, v_max := (s_opt ${\displaystyle \cup }$ s_tmp, v_max + v_tmp)
   retourner (s_opt, v_max)

La validité de cet algorithme par programmation dynamique repose sur le respect de la propriété de monotonie (qui est un affaiblissement du principe de Bellman)[32]. On dit qu'un critère de décision ${\displaystyle V}$ respecte la propriété de monotonie si et seulement si :

${\displaystyle \forall (L_{1},L_{2},L_{3})\in \mathbb {L} _{X}^{3}}$ et ${\displaystyle \forall \alpha \in ]0,1[}$ on a ${\displaystyle V(L1)\geq V(L_{2})\Rightarrow V(\alpha L_{1}+(1-\alpha )L_{3})\geq V(\alpha L_{2}+(1-\alpha )L_{3})}$

Dans le cadre du risque cette propriété est vérifiée dès lors que l'axiome d'indépendance est respecté par le critère ${\displaystyle V}$. Cet axiome rend possible toute approche par programmation dynamique pour déterminer une stratégie optimale au sens de ${\displaystyle V}$.

Les critères non-EU ne sont généralement pas compatibles avec l'axiome d'indépendance. Il est rare alors de pouvoir appliquer une approche par induction arrière pour déterminer une stratégie optimale. Pire, la stratégie construite ainsi peut être dominée stochastiquement au premier ordre par une autre stratégie disponible[29]^,[33]. Dans le cadre du modèle RDU, le problème est même NP-difficile et il faut alors utiliser des algorithmes d'optimisation combinatoire pour déterminer la stratégie optimale vue de la racine de l'arbre[31]. Ces approches algorithmiques sont du ressort de la théorie de la décision algorithmique.

L'échec de la programmation dynamique pour la détermination d'une stratégie optimale est souvent révélateur de certaines propriété normatives qui sont violées par le critère. La violation de ces propriétés a fait couler beaucoup d'encre et a relancer le débat sur la légitimité de l'axiome d'indépendance. Les arguments exposés ont fait l'objet d'une littérature conséquente mais assez disparate dans le sens où les différences terminologiques et conceptuelles d'un auteur à l'autre rendent très difficile la lisibilité[34]. Ainsi, il en est ressorti que le rejet de l'axiome d'indépendance pose des difficultés normatives dans un cadre de décision séquentielle. En effet, en décision séquentielle, un axiome qui se pose naturellement est celui de la cohérence dynamique. Cet axiome stipule que les préférences d'un décideur sont identiques à tout instant. Ainsi, un décideur est dit cohérent dynamiquement s'il est cohérent dans le temps et ne change pas d'avis alors que l'ensemble de l'information reste inchangée (car la résolution de l'incertitude est prise en compte ex-ante dans la détermination de la stratégie optimale).

Il est démontré que l'axiome de cohérence dynamique est vérifié si l'axiome d'indépendance est vérifié[35]^,[36]. Dans la théorie du conséquentialisme, l'axiome d'indépendance découle de trois axiomes de rationalité dynamique : l'axiome de cohérence dynamique, l'axiome conséquentialiste et l'axiome de réduction des loteries composées. L'axiome de cohérence dynamique est une propriété normative fortement désiré dans la rationalité du décideur. L'axiome de réduction de loterie a été très peu étudié dans la littérature, peu ou pas de pistes ne remettent en cause son utilisation (mais la perte de l'ordre d’exécution des événements lors de la réduction est un sujet qui a été pointé méritant d'être approfondi[6]) . Cependant le rejet de l'axiome conséquentialiste semble naturel dans plusieurs situations de choix[37], et il est démontré que le rejet de l'axiome conséquentialiste ne remet pas en cause la validité de l'axiome de cohérence dynamique[38]. La différence entre un décideur ${\displaystyle a}$ qui adopte un comportement conséquentialiste et un décideur ${\displaystyle b}$ qui adopte un comportement non-conséquentialiste, vient du fait que le décideur ${\displaystyle b}$ accorde encore de l'importance à un risque déjà encouru contrairement au décideur ${\displaystyle a}$ qui ne tient plus compte d'un risque une fois qu'il a été encouru. Le comportement d'un décideur cohérent dynamiquement et non-conséquentialiste est connu dans la littérature sous le nom de choix résolu. Le choix résolu désigne le comportement d'un décideur qui se fixe un plan de décision et n'en dévie plus par la suite (i.e., qui s'impose de rester cohérent dynamiquement).

Les approches algorithmiques mettant en œuvre le choix résolu pour des critères rejetant l'axiome conséquentialiste ont été proposées dans la littérature sous le nom de veto-process[39].

• Intelligence artificielle
• Théorie de la décision
• Théorie des jeux
• Théorie du choix social
• Planification (intelligence artificielle)
• Utilité (économie)
• Paradoxe de Newcomb

• Cet article est partiellement ou en totalité issu de l'article intitulé « Théorie de la décision » (voir la liste des auteurs).

• Portail des mathématiques
• Portail de l'informatique théorique
• Portail des probabilités et de la statistique
• Portail de l’économie
• Portail de la sociologie