Estimation stochastique en mécanique des fluides

Pour comprendre un écoulement turbulent en mécanique des fluides, il y a deux stratégies possibles:

• Effectuer des visualisations expérimentales. Par exemple, une expérience en soufflerie permet de visualiser le champ de vitesse (vélocimétrie par image de particules PIV) et de récupérer certaines grandeurs d'intérêts (signaux de vitesse ou de pression).

• Effectuer un calcul numérique. L'objectif est de résoudre les équations de Navier-Stokes en choisissant une modélisation plus ou moins fine de la turbulence.

Chacune des approches présente des avantages et des inconvénients:

• L'approche expérimentale présente l'avantage d'être le reflet de la réalité et de ne pas reposer sur un modèle mathématique. Toutefois, il est difficile de caractériser entièrement l'écoulement. Par exemple, la PIV permet uniquement d'observer l'écoulement sur certaines fenêtres d'observation avec une résolution en temps dépendant de la cadence du LASER[1]. Un autre exemple concerne l'acquisition de signaux temporels: en plus d'être limité à des mesures ponctuelles, les méthodes de mesures peuvent être intrusives (fil chaud).
• L'approche numérique présente l'avantage d'être flexible: une fois le champ calculé, l'information peut-être visualisée n'importe où. Toutefois, les résultats dépendent fortement du degré de modélisation retenue. Dans le cas d'un calcul RANS, presque toute la turbulence est modélisée, au détriment d'une bonne résolution spatiale et temporelle. Dans le cas d'une DNS, toute la turbulence est résolue, d'un point de vue spatial et temporel, mais cela nécessite un très grand coût ordinateur[3].

De façon générale, il est donc difficile de récupérer à la fois l'information spatiale et l'information temporelle d'un écoulement.

L'estimation stochastique a été introduite par Adrian en 1975[4]. Dans son article, il propose d'approximer le champ de vitesse d'un écoulement par une moyenne d'ensemble conditionnée par un ensemble de réalisations ponctuelles. Ces réalisations peuvent être homogènes au champ de vitesse ou non. En développant la moyenne conditionnelle sous la forme d'une série de Taylor, le champ est approximé par une combinaison polynomiale des réalisations dans le champ.

Si l'estimation stochastique est le nom particulier donné dans le cadre de la mécanique des fluides, la méthode est bien plus générale et fait partie de la classe des régressions en apprentissage automatique.

L'estimation stochastique a été utilisée pour étudier de la turbulence isotrope[5], des couches limites turbulentes[6], des jets axisymmétriques[7], des marches descendante[8], des cavités ouvertes[9] ou pour des stratégies de contrôle[10].

Dans la suite, l'événement ${\displaystyle E_{{\vec {x}}_{i}}(t)}$ désigne aussi bien ${\displaystyle p_{{\vec {x}}_{i}}(t)_{E}}$ que ${\displaystyle p_{{\vec {x}}_{i}}(t)_{V}}$ avec ${\displaystyle i}$ décrivant les ${\displaystyle n}$ capteurs retenus placés en ${\displaystyle {\vec {x}}_{i}}$. Par ailleurs, on suppose connaître ${\displaystyle M}$ échantillons pour chaque grandeur.

L'idée de l'estimation stochastique est d'approximer le champ complet par une moyenne conditionnelle entre le champ complet réel et les événements de pression[4]. Cette estimation s'écrit donc:

${\displaystyle {\tilde {u}}({\vec {x}},t)=<u({\vec {x}},t)|E_{{\vec {x}}_{1}},...,E_{{\vec {x}}_{n}}>=f(E_{{\vec {x}}_{1}},...,E_{{\vec {x}}_{n}})}$

Par développement de Taylor autour de 0 (car les grandeurs sont fluctuantes), on peut écrire à l'ordre 1 (LSE pour Linear Stochastic Estimation) et à l'ordre 2 (QSE pour Quadratic Stochastic Estimation)[11]:

${\displaystyle LSE:{\tilde {u}}({\vec {x}},t)\approx \sum _{i=1}^{n}{A({\vec {x}}_{i},{\vec {x}})E_{{\vec {x}}_{i}}(t)}}$

${\displaystyle QSE:{\tilde {u}}({\vec {x}},t)\approx \sum _{i=1}^{n}{A({\vec {x}}_{i},{\vec {x}})E_{{\vec {x}}_{i}}(t)}+\sum _{i=1}^{n}{\sum _{j=1}^{n}{B({\vec {x}}_{i},{\vec {x}}_{j},{\vec {x}})E_{{\vec {x}}_{i}}(t)E_{{\vec {x}}_{j}}(t)}}}$

Les coefficients de la régression sont les ${\displaystyle A=A({\vec {x_{i}}})}$ dans le cas linéaire et ${\displaystyle A=[A({\vec {x_{i}}}),B({\vec {x_{i}}},{\vec {x_{j}}})]}$ dans le cas quadratique. Ils sont calculés par moindres carrés c'est-à-dire qu'ils sont solution du problème de minimisation: ${\displaystyle \min _{A}||U-EA||_{2}}$.

La solution générale est donnée par[12]:

${\displaystyle A=[E^{T}E]^{-1}E^{T}U}$

Avec:

• ${\displaystyle A}$ le vecteur des coefficients de régression.
• ${\displaystyle U}$ le vecteur vitesse.
• ${\displaystyle E}$ une matrice qui contient les événements. Dans le cas quadratique, le produit des événements est considéré comme un nouvel événement.

À noter que la solution s'écrit également ${\displaystyle A=E^{+}U}$avec ${\displaystyle E^{+}}$la pseudo-inverse de ${\displaystyle E}$.

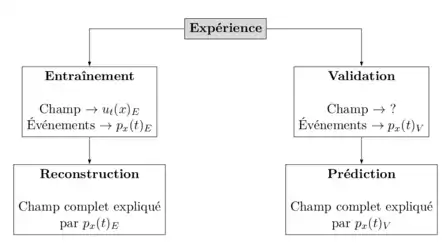
La figure suivante illustre le principe d'estimation stochastique en ne considérant qu'un seul capteur de pression.

• Le premier encadré correspond à l'expérience. Les carrés bleus sont les champs de vitesse résolus en espace à des temps précis (temps PIV) tandis que la flèche correspond au signal de pression récupéré en un point de l'écoulement mais résolu en temps.
• Le second encadré correspond à de la reconstruction. L'objectif est de calculer les carrés rouges i.e. les champs de vitesse résolus en espace à des temps autres que les temps PIV. Ces champs de vitesse sont entièrement déterminés par le signal de pression de l'expérience, pourvu que les corrélations entre les carrés bleus et le signal aient été calculés.
• Le troisième encadré correspond à de la prédiction. On utilise les corrélations calculés avec les données du premier encadré mais cette fois, les carrés verts seront calculés uniquement à partir du signal de validation.

• Portail de la physique