Duplication du cube

La duplication du cube est un problème classique de mathématiques. C'est un problème géométrique, faisant partie des trois grands problèmes de l'Antiquité, avec la quadrature du cercle et la trisection de l'angle[1],. Ce problème consiste à construire un cube dont le volume est deux fois plus grand qu'un cube donné, à l'aide d'une règle et d'un compas.

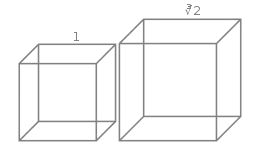
Un cube de volume unitaire (gauche) et un cube de volume 2 (droite).
À partir de la figure de gauche, il est impossible de construire par les moyens géométriques traditionnels le cube de droite.

Ce problème revient à multiplier l'arête du cube par la racine cubique de 2, la constante délienne. Il est impossible de construire un tel cube à la règle et au compas (Théorème de Wantzel).

Origine

Le problème — appelé aussi problème de Délos — a son origine dans une légende rapportée entre autres par Ératosthène dans Le Platonicien et par Théon de Smyrne[2] dans son Arithmétique. Les Déliens, victimes d'une épidémie de peste, demandèrent à l'oracle de Delphes comment faire cesser cette épidémie. La réponse de l'oracle fut qu'il fallait doubler l'autel consacré à Apollon, autel dont la forme était un cube parfait. Les architectes allèrent trouver Platon pour savoir comment faire[1]. Ce dernier leur répondit que le dieu n'avait certainement pas besoin d'un autel double, mais qu'il leur faisait reproche, par l'intermédiaire de l'oracle, de négliger la géométrie[3].

Postérité scientifique
Construction de 3√2 à la règle graduée et au compas. Construire un triangle équilatéral ABC, et le point D symétrique de A par rapport à B ; tracer la droite (DC). De A, mener avec la règle graduée une droite AH de façon qu'elle coupe les droites (DC) en G, et (BC) en H, et que GH soit égale au côté du triangle ABC. Alors GA = 3√2.

La question intéressa nombre de mathématiciens, par exemple Hippias d'Élis, Archytas de Tarente, Ménechme, Eudoxe de Cnide, Hélicon de Cyzique et Eutocios d'Ascalon. Plusieurs solutions furent proposées par intersection de coniques ou par intersection de figures spatiales, par exemple Archytas proposa l'intersection entre un cône et un tore. D'Alembert écrivit en 1760 qu'aucune solution plane ne fut trouvée avec la seule utilisation de la règle et du compas[4].

En 1837, Pierre-Laurent Wantzel établit un théorème donnant la forme des équations des problèmes solubles à la règle et au compas. Il démontre que 3√2 n'est pas constructible. La duplication du cube est donc impossible à réaliser à la règle et au compas. Elle devient possible avec d'autres méthodes, telles que l'utilisation de la règle graduée et du compas, ou par pliage de papier.

Notes et références

Notes

    Références
    1. Cf. Robert Baccou, Histoire de la science grecque, de Thalès à Socrate, Paris, Aubier, , 256 p.
    2. Théon de Smyrne, « De l'utilité des mathématiques », Cahiers d'Histoire des Mathématiques et d'Epistémologie, IREM de Poitiers, fascicule 1, déc. 1997, p. 9.
    3. González Urbaneja et Mangin 2018, p. 20-21.
    4. D'Alembert écrivit en 1760 dans son Encyclopédie : « Les Géomètres cherchent depuis deux mille ans une méthode pour trouver géométriquement deux moyennes proportionnelles entre deux lignes données, c'est-à-dire, en n'employant que la ligne droite et le cercle ; car du reste ce problème est abondamment résolu ; et particulièrement la résolution que l'on en donne par les sections coniques, en faisant, par exemple, qu'un cercle et une parabole s'entrecoupent suivant une certaine loi, est une solution très géométrique de ce problème. En le réduisant à une équation algébrique, il paraît impossible qu'on le résolve jamais avec le seul secours de la ligne droite et du cercle ; car on arrive toujours à une équation du troisième degré, qu'il n'est pas possible de construire avec la ligne droite et le cercle. Les anciens résolvoient ce problème méchaniquement par le moyen du mésolabe décrit par Eutocios : et plusieurs d'entr'eux ont tâché d'en donner la démonstration : d'autres, comme Ménechme, résolvoient ce problème par les lieux solides : d'autres, par des mouvements composés, comme Platon, Archytas, Pappos et Sporos : d'autres enfin, en tâtonnant, comme Héron et Apollonios de Perga. »

    Voir aussi

    Bibliographie

     : document utilisé comme source pour la rédaction de cet article.

    • Henri Lebesgue, Leçons sur les constructions géométriques, Paris, Gauthier-Villars, (réimpr. 2003), 318 p., chap. 1 (« La solution des problèmes fondamentaux : trisection de l'angle, duplication du cube »). 
    • (en) Eli Maor et Eugen Jost, Beautiful Geometry, Princeton, Princeton University Press, , 187 p. (ISBN 978-0-691-15099-4, lire en ligne), p. 81-83
    • Abel Rey, L’Apogée de la science technique grecque, vol. 5 : L’essor de la mathématique, Albin Michel, coll. « L’Évolution de l'Humanité ». .
    • Pedro Miguel González Urbaneja et Magali Mangin (Trad.), Le royaume des coniques : Apollonios, Barcelone, RBA Coleccionables, , 163 p. (ISBN 978-84-473-9619-1). 

    Articles connexes

    Lien externe

    (en) Eric W. Weisstein, « Delian Constant », sur MathWorld

    • Portail de la géométrie
    Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.