Algèbre géométrique
En mathématiques, l’algèbre géométrique regroupe des méthodes géométriques, utilisées par les Grecs de l'Antiquité, pour établir des résultats maintenant classés dans la branche mathématique appelée algèbre. Ces techniques permettent la mise en évidence des propriétés élémentaires de la multiplication, d’effectuer des calculs comme la somme des premiers nombres entiers, ou impairs. Elles permettent d’établir des résultats comme des identités remarquables ou de résoudre une équation du second degré. L’algèbre géométrique fournit aussi des méthodes de résolution plus complexes, comme celles qui montrent l’existence de nombres irrationnels.

Si ces méthodes sont anciennes et correspondent à une vision des mathématiques qui n'est plus la nôtre, elles sont toujours utilisées dans l’enseignement, soit pour donner des preuves simples de certains résultats, soit pour développer une conscience intuitive de résultats qu'une présentation algébrique rendrait plus abstraits.
Le terme « algèbre géométrique » provient d’un livre de l’historien des sciences Hieronymus Georg Zeuthen écrit en 1902. Il est popularisé par Paul Tannery l'année suivante. Les livres II et VI des Éléments d'Euclide en forment le cœur. Si une lecture contemporaine permet d'interpréter de manière algébrique les résultats démontrés ainsi, tel n'était néanmoins pas la lecture des Grecs qui n'avaient pas découvert les principes fondateurs de l'algèbre. Pour cette raison, cette lecture apocryphe de la science grecque est parfois critiquée.
L'expression « algèbre géométrique » est aussi utilisée en mathématiques pures, elle correspond alors à un concept moins élémentaire. Elle désigne une branche contemporaine des mathématiques consistant à associer une géométrie à une structure d'algèbre. Cet aspect est traité dans l'article Algèbre géométrique (structure). Les termes géométrie algébrique désignent une branche différente des mathématiques, constituée d'un savoir essentiellement acquis aux XIXe et XXe siècles et toujours d'actualité en recherche mathématique.
Propriétés de la multiplication
Nombre entier positif
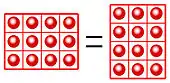
On peut remarquer que 4 × 3 est égal à 3 × 4 et, de manière plus générale « le produit de nombres entiers ne dépend pas de l’ordre des facteurs[1] ».
Pour se persuader de l’exactitude de ce résultat, on peut considérer des petits carrés, tous de même dimension, assemblés en rangées de 3. En accolant verticalement 4 rangées de 3, on obtient un rectangle de base 4 côtés de petits carrés et de hauteur 3. Ce rectangle, illustré sur la figure de gauche, contient 4 × 3 = 12 petits carrés. Appliquer un quart de tour au rectangle ne modifie pas le nombre de petits carrés le composant, ce qui montre que le résultat de 4 × 3 correspond au nombre de petits carrés composant le rectangle associé à l’opération 3 × 4. Ce résultat ne dépend pas des valeurs 3 et 4, on peut choisir deux nombres entiers quelconques que l’on peut noter a et b. L’égalité qui s’écrit de la manière suivante traduit ce que l’on appelle la commutativité de la multiplication :

La commutativité de la multiplication n’est pas l’unique propriété s’illustrant à l’aide de la géométrie. La figure de droite peut se lire de deux manières différentes. Tout d’abord, le grand rectangle est la somme des aires des rectangles bleus et rouges. Le raisonnement précédent montre que son aire est égale à 9 × 3 + 9 × 4. On peut le voir aussi comme un unique rectangle, s'il l'on ne tient pas compte des couleurs, d’aire égale à 9 × (3 + 4). Ces deux écritures correspondent donc au même nombre. Une fois encore, le résultat est vrai non seulement pour les nombres 9, 3 et 4, mais aussi pour n’importe quel ensemble de trois nombres, que l’on peut noter a, b et c. On obtient le résultat suivant, appelé distributivité de la multiplication par rapport à l’addition.
Ainsi, l'usage de la géométrie et plus spécifiquement le calcul des aires permet d'établir certaines propriétés de la multiplication. Ce principe est la base de l'algèbre géométrique[2].
Fraction
Pour faire de la géométrie, les nombres entiers ne suffisent pas toujours. Une longueur peut être égale à la moitié d'une autre. Les Grecs ont donc été amenés à établir les règles opératoires régissant les fractions[Note 1]. Une fois encore le calcul des aires est utile. Pour illustrer cette approche, cherchons à additionner 1/6 et 4/9. Considérons pour cela un rectangle dont l’aire est égale à 1. On choisit deux quadrillages qui décomposent le rectangle en petits rectangles identiques. On choisit ces quadrillages compatibles, c'est-à-dire que la superposition des quadrillages est encore un quadrillage en petits rectangles tous identiques, comme l’illustre la figure ci-dessous :

La première représentation du rectangle montre que la fraction 1/6 est représentée par un quadrillage découpant le rectangle en 6 petits rectangles, la superposition des quadrillages en crée 18 et 1/6 = 3/18. On obtient finalement les égalités :
D'une manière générale, si a, b, c, et d sont des nombres entiers tels que ni b ni d ne sont nuls, alors :
L’article détaillé montre comment la démarche permet de déterminer toutes les règles opératoires des fractions.
Arithmétique géométrique
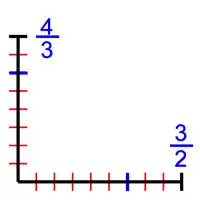
À l’aube des mathématiques grecques et jusqu’au mathématicien Pythagore, l’on pensait que toutes les longueurs pouvaient s’exprimer par ce que l’on appelle maintenant des fractions, ce que Tannery exprime de la manière suivante : « les Pythagoriciens sont partis de l’idée, naturelle à tout homme non instruit, que toute longueur est nécessairement commensurable à l’unité[3]. ». Ces mathématiciens en conclurent que, pour étudier une figure géométrique, l'on pouvait toujours choisir une longueur unité telle que tous les segments représentés sur la figure aient des longueurs qui s’expriment comme des nombres entiers. La figure de droite illustre cette situation. Elle représente deux segments de longueur 4/3 et 3/2, si l'unité choisie est indiquée par la graduation bleue. L'unité de la graduation rouge est de longueur le sixième de la bleue, avec la graduation rouge, les longueurs sont entières et égales à 8 et 9.
Cette remarque et certaines figures géométriques permettent d’établir des résultats sur les nombres entiers, résultats qui entrent dans la branche mathématique appelée arithmétique. Zeuthen considère ces techniques comme de l’arithmétique géométrique. Il estime que c'est une branche de l’algèbre géométrique car les démarches sont analogues[4],[5],[6].
Pour faire de l'arithmétique géométrique les représentations sont de même nature que celle du paragraphe Nombre entier, mais il est possible de les simplifier. Les Grecs avaient remarqué que tracer les rectangles était inutile. Les pastilles à l’intérieur des carrés, qui étaient alors des galets[7], suffisaient. La méthode consiste à représenter un nombre à l'aide d'un assemblage de pastilles selon une figure géométrique. L'association du nombre et de la figure est appelée un nombre figuré. Celle utilisée au paragraphe précédent pour représenter 12 est appelée nombre rectangle. Il existe plusieurs figures cataloguées[d 1].

Somme des premiers nombres
En accolant deux triangles égaux comme sur la figure ci-contre, on obtient un rectangle dont la longueur est d'une unité supérieure à sa largeur (son aire est appelée un nombre oblong). L'article détaillé montre qu'on en déduit la formule suivante[8] :
Nombre carré

Un nombre carré est un nombre égal à un certain entier multiplié par lui-même. Par exemple, 9 est un nombre carré car 3 × 3 = 9. Il se présente de manière figurée comme un carré. Pour établir la liste des premiers carrés, l’arithmétique géométrique peut être utile. On suppose, par exemple, connue la liste jusqu’à 7 × 7 = 49. Pour trouver la valeur du carré suivant, de côté 8, on raisonne à l’aide de la figure de gauche. Le nombre 8 × 8 peut être vu comme la somme de 7 × 7 correspondant aux billes rouges, de 7 correspondant aux billes vertes et 8 correspondant aux billes bleues. De manière générale, on dispose de l’égalité[d 2] :

Établir la liste des premiers nombres carrés est un vieil exercice, déjà réalisé par les mésopotamiens. À cette époque, la numération était en base 60. Réaliser des multiplications comme nous le faisons maintenant aurait supposé d’apprendre les tables de multiplication jusqu’à 60, exercice de mémorisation difficile et que l’on n'imposait pas aux écoliers mésopotamiens[9]. Les tables de carrés, qui existaient alors, étaient bien utiles. Par exemple, la multiplication de 15 par 29 donne[d 3] :
Les Grecs héritèrent du savoir mésopotamien et ajoutèrent leur propre interprétation qui leur permit de trouver d’autres résultats. Ils avaient remarqué que, si le côté d'un nombre carré est pair, le nombre carré l'est aussi, car il se décompose en la somme de deux nombres rectangles égaux dont la base est égale à deux fois la hauteur. La logique géométrique permet de comprendre que si le côté est de longueur impair, l’aire l’est aussi. La figure de droite l’illustre sur l’exemple 15 × 15. La représentation du nombre carré montre qu’il est somme d’un carré, en rouge sur la figure, qui est pair (il est composé d’autant de pastilles claires que foncées), d’un nombre pair (les pastilles bleues, qui sont graphiquement divisées en deux parties égales) et d’une pastille verte, isolée. Ainsi 15 × 15 est la somme d’un nombre pair (les pastilles rouges et les bleues) et de 1, ce qui est un nombre impair[10].
Triplet pythagoricien

À l’aide de la figure permettant de calculer la liste des carrés, les Grecs définirent un nouveau nombre figuré, le nombre gnomon. Les pastilles bleues de la figure de gauche correspondent à un nombre gnomon : 9. Cette figure de gauche montre qu’un carré est formé d'une suite de nombres gnomons, correspondant à la suite des premiers nombres impairs[d 4]. Ce que l’on peut encore traduire par l’égalité :
Ce résultat permet de construire des triplets pythagoriciens si, comme sur la figure de gauche, le dernier gnomon est un carré parfait. L’égalité issue de cette figure s’écrit :
Or la somme des nombres entre parenthèses correspond à un nombre carré ; l’égalité s’écrit encore :
Cette observation permet de construire des séries de trois nombres a, b et c, vérifiant a2 + b2 = c2, que l’on appelle triplet pythagoricien. À l'aide du théorème de Pythagore, il devient possible de construire des triangles rectangles (à côtés entiers)[11]. Si, au lieu de choisir une largeur 1 pour le gnomon, on lui attribue une largeur quelconque, on peut trouver une méthode qui donne tous les triplets pythagoriciens. Elle est proposée dans le livre X des Éléments d'Euclide[12].
Somme des cubes
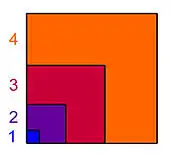
Les nombres cubiques sont construits comme les carrés, à la différence que cette fois-ci le nombre représente le volume et non la surface. Les quatre premiers nombres cubiques sont 1 = 13, 8 = 23, 27 = 33 et 64 = 43. Le raisonnement suivant montre que la somme des premiers nombres cubiques est toujours un nombre carré.
Dans la figure ci-contre, le côté du plus grand carré a pour longueur le nombre triangulaire 1 + 2 + 3 + 4 = 10. Ce carré est décomposé en une somme de gnomons dont la largeur vaut 1, puis 2, puis 3, puis 4. Calculons l'aire du dernier. Cette zone orange est composée d'un carré de côté 4 et de deux rectangles de largeur 4 et de longueur 1 + 2 + 3 = 6. L'aire du gnomon est donc égale à 2 × 4 × 6 + 42 = 3 × 42 + 42 = 43.
Ce raisonnement est vrai pour tous les nombres gnomons de la figure : le raisonnement précédent montre que le n-ième vaut
On en déduit que la somme des n premiers nombres cubiques est le carré du n-ième nombre triangulaire.
Équation du second degré
Introduction par l'exemple
À l'époque de Pythagore, il est probable que les Grecs savaient construire rigoureusement un pentagone régulier[13]. A priori, cette construction semble ne concerner que la géométrie, et c'est ainsi que les Grecs le concevaient. Une lecture moderne indique que cette question est intimement liée à la résolution d'une question algébrique, à savoir la résolution d'un problème du second degré[14].
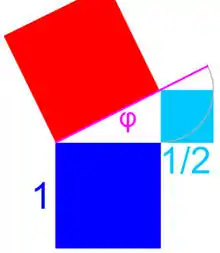
Construire cette figure suppose la connaissance des proportions du triangle isocèle formé par deux côtés adjacents du pentagone. Si l'on choisit l'unité égale à la longueur d'un côté et si φ désigne la base du triangle, qui correspond à une diagonale du pentagone, la proportion s'exprime de la manière suivante :
Du point de vue grec sous la forme (1), la question posée est géométrique, c'est celle de la détermination d'une proportion, qu'Euclide appelle d'extrême et de moyenne raison. Du point de vue moderne et sous la forme (2), la question posée est algébrique, c'est celle de la résolution d'une équation du second degré ayant pour unique solution positive le nombre d'or. Il est possible qu'Hippase de Métaponte, l'auteur probable de la construction[15], ait utilisé une méthode importée de Babylone[16], une fois encore à base d'un gnomon.
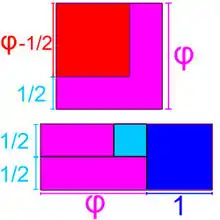
L'égalité φ2 = φ + 1 directement issue de l'égalité (1) se lit de la manière suivante : un carré de côté φ possède la même aire qu'un rectangle de base φ + 1 et de hauteur 1, résultat représenté sur la figure de gauche. En retranchant au carré et au rectangle, l'aire d'un gnomon du hauteur φ et de largeur 1/2, on remarque qu'un carré de côté φ – 1/2 possède une aire égale à la somme de celle d'un carré de côté 1 et de celle d'un carré de côté 1/2. Obtenir la longueur φ devient aisé avec le théorème de Pythagore, elle est construite sur la figure de droite.
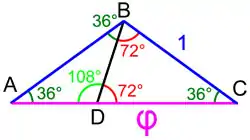
Soit ABC trois sommets consécutifs d'un pentagone régulier de côtés de longueur 1. Un polygone convexe de n côtés a, pour valeur de la somme de ses angles, (n – 2) × 180°, soit pour un pentagone 540°. Comme celui étudié ici est régulier, l'angle ABC est de mesure 540° / 5 = 108°. Les deux autres angles BCA et CAB sont égaux car le triangle est isocèle. Comme la somme des mesures des angles d'un triangle est égale à 180°, les deux autres angles ont pour mesure 36°. On obtient le triangle de la figure de droite.
Si l'on trace la droite passant par B et divisant l'angle ABC de 108° en deux angles comme sur la figure de droite, l'un de 36° et l'autre de 72°, on divise le triangle initial en deux triangles isocèles ABD et DBC. Une analyse des angles montre que le triangle ABC est semblable au triangle ABD. Il est alors possible d'appliquer le théorème de Thales en remarquant que AB = 1, AC = AD + DC = φ et BC = CD = 1 car le triangle DBC est isocèle. Finalement : AD = φ – 1, et l'on obtient :
Identité remarquable
.jpg.webp)
La résolution d'une équation du second degré, dans le cas général, se résout à l'aide de trois identités remarquables, développant les expressions (a + b)2, (a – b)2 et (a + b)(a – b)[Note 2]. Elles se démontrent à l'aide des propriétés algébriques de l'addition et de la multiplication. Pour les Grecs, ces résultats sont des vérités géométriques, qui se démontrent à l'aide d'un carré, en bleu sur la figure de droite et d'un gnomon, en vert et rouge.
Pour établir la formule suivante, on considère la figure de droite :
La longueur bleue représente a et la rouge b. L'expression (a + b)2 est égale à l'aire du grand carré de côté a + b. Il est possible de le décomposer en trois parties : la zone bleue, correspondant à un carré de côté a et d'aire a2; la zone rouge, correspondant à un carré de côté b et d'aire b2 et la zone verte, correspondant à deux rectangles de longueur a et de largeur b. Chaque rectangle de la zone verte est d'aire égale à ab, la zone verte est d'aire 2ab. On retrouve bien l'identité remarquable (1).
On établit de même l'identité :
Cette fois-ci, la longueur bleue désigne a – b et la rouge b. L'expression (a – b) correspond maintenant à l'aire du carré bleu. L'aire du carré bleu peut être vue comme la différence entre le grand carré, maintenant de côté a et les deux zones vertes et la zone rouge. Le rectangle composé d'une zone verte et du carré rouge a pour aire a.b. Si l'on retranche à l'aire du carré de côté a deux aires d'un rectangle de longueur a et de largeur b, on trouve l'aire du carré bleu ôtée de celle du carré rouge, ce qui donne l'identité suivante, dont on déduit une égalité équivalente à (2) :
L'identité (3) se démontre à l'aide de la même figure :
On utilise les mêmes conventions que celles établissant l'identité (2). L'aire de la surface a2 – b2 correspond à l'aire du grand carré ôtée de l'aire du carré rouge, c'est-à-dire à l'aire du carré bleu additionnée à l'aire des deux rectangles verts. Le rectangle composée de la zone bleue et d'une zone verte correspond à un rectangle d'aire a(a – b). Si l'on déplace un des deux rectangles verts pour le positionner de long du deuxième rectangle vert de manière à former un nouveau rectangle, on trouve un rectangle de longueur (a + b)(a – b). Ce rectangle est d'aire égale à celle du grand carré ôtée de l'aire du carré rouge, ce qui démontre l'identité (3).
Ainsi, toutes les identités remarquables utilisées pour résoudre des équations du second degré s'interprètent et se démontrent de manière géométrique. En conséquence, toutes les équations du second degré peuvent se résoudre de manière géométrique. Cette lecture, démontrant l'équivalence du contenu mathématique des identités remarquables avec un savoir géométrique présent dans le livre II des Éléments d'Euclide est l'œuvre de Zeuthen[17].
Résolution d'une équation du second degré
On recherche à résoudre l'équation suivante[18] :
La méthode s'inspire directement de calculs analogues à ceux permettant d'établir les identités remarquables. Elle est illustrée sur la figure ci-dessous.
.jpg.webp)
Dans un premier temps, on construit un carré de côté a/2. par hypothèse, ce carré est d'aire plus grande que c. On retranche au carré, en bas à gauche un petit carré de telle manière que la surface rouge et violette soit d'aire exactement égale à c.
Dans un deuxième temps, on remarque que la longueur x obtenue est aussi la hauteur du rectangle rouge de gauche. Il est donc possible de déplacer la zone violette sur la figure de droite et d'ajouter à gauche de cette figure un carré de côté x. L'aire rouge et violette est, d'après la construction de la figure de gauche, égale à c. Par construction, la figure de droite est d'aire égale à c + x2. Cette aire est aussi égale à a.x, car la figure est un rectangle de base a et de hauteur x, ce qui donne la solution de l'équation. Ce mode de résolution provient directement du livre II des Éléments d'Euclide[19].
Irrationalité
Les Grecs finirent par s'apercevoir que leur postulat initial était faux. Toutes les longueurs ne s'expriment pas comme une fraction de deux nombres entiers. Une question, naturelle pour un pythagoricien, est la détermination de la fraction de nombres entiers décrivant la proportion entre une diagonale et son côté, pour un pentagone ou un carré. Ce rapport n'est pas une fraction de nombre entier. Les méthodes de l'algèbre géométrique sont adaptés pour appréhender cette question. En termes modernes, la question est algébrique car elle correspond à la nature d'une solution d'une équation du second degré[20].
Les Pythagoriciens développaient le culte du secret à propos de leurs savoirs, il est en conséquence difficile de connaître précisément quand, par qui et avec quelles méthodes la découverte puis la démonstration ont été faites[21]. Plusieurs hypothèses sont imaginées et, à ce jour, aucune ne fait l'unanimité[22].
Une découverte à l'aide du pentagone ?

L'historien Kurt von Fritz émet l'hypothèse suivante[23] : Hippase, après avoir trouvé comment construire le pentagone, aurait cherché à déterminer la section d'extrême et de moyenne raison, c'est-à-dire le rapport entre une diagonale et un côté d'un pentagone régulier. Il imagine[24] que cette section est une fraction n/m de deux nombres entiers. Une procédure pour trouver ces valeurs n et m consiste à construire un rectangle de base n et de hauteur m. On cherche à emplir ce rectangle de carrés de côté le plus grand possible. La première valeur du côté est m et on peut placer un unique carré, en rouge sur la figure.
Après avoir placé le carré rouge, la zone restante est un carré de côté m et n – m. En multipliant par n/m, on remarque que le carré est homothétique à un carré de hauteur m et de base n. Ce résultat est une conséquence de l'égalité 1/(φ – 1) = φ. On en déduit que l'on peut ensuite placer un unique carré, en bleu foncé sur la figure et de côté n – m. On en déduit surtout que la procédure ne s'arrête jamais !
Cette procédure, connue depuis les babyloniens sur le calcul du rapport entre la diagonale et le côté d'un carré[25], permet de donner une suite de fractions qui approxime de mieux en mieux la fraction φ[Note 3]. On obtient : 1, puis 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21 ..., c'est-à-dire des fractions de plus en plus proches de φ, avec des numérateurs et des dénominateurs qui ne cessent de croître. Ce comportement n'a aucun sens, les dénominateurs ne devraient jamais dépasser m. Les carrés rouge puis bleus ont nécessairement des côtés entiers. L'historien Maurice Caveing en conclut qu'il est raisonnable de penser que ces observations ont permis la réalisation d'une révélation stupéfiante : le fait que toutes les grandeurs ne sont pas des fractions[26],[Note 4].
Des fins possibles de la démonstration
.jpg.webp)
Il existe d'autres manières de conclure à partir de la construction précédente. On suppose toujours que φ est un nombre rationnel, noté n/m, et on construit un pentagone régulier de côté m et de diagonale n. La figure de droite montre comment construire un nouveau pentagone, de côté n – m et de diagonale m, le côté et la diagonale du nouveau pentagone sont toujours des entiers, mais cette fois-ci plus petits. L'on peut ainsi continuer indéfiniment. La suite des côtés forment alors une liste d'entiers positifs strictement décroissante et infinie, ce qui est impossible. Un tel raisonnement s'appelle en mathématique une descente infinie.
Il existe aussi une manière plus rapide et plutôt plus simple de conclure. Avec les mêmes hypothèses, on choisit, pour valeur de n/m, une représentation irréductible, c'est-à-dire que m est la plus petite valeur que doit prendre le côté du pentagone pour que le diamètre soit de longueur entière. Le pentagone en rouge de la figure de droite montre qu'il est possible de construire un pentagone de côté n – m et de diagonale entière. Cette contradiction permet de conclure.
Il existe un consensus relativement vaste chez les historiens pour admettre qu'Hippase n'a pas pu terminer la démonstration. Par exemple, pour la descente infinie, Caveing remarque que : « Ce qui manque à la démonstration c'est seulement l'axiome d'Archimède, ou un lemme équivalent, qu'au témoignage d'Archimède lui-même on n'a pas le droit de faire remonter plus haut qu'Eudoxe de Cnide[27] ». Ainsi, Caveing pense qu'à la période d'Hippase, aucune découverte scientifique fructueuse[26] n'était possible.
Racine carrée de deux
.jpg.webp)
La logique présentée pour le pentagone s'applique aussi pour la diagonale du carré. On en retrouve des traces dans les livres d'Euclide. La preuve par la descente infinie se trouve dans le livre X, à la proposition 117. La démonstration que la fraction continue d'un nombre rationnel est finie se trouve dans le livre VII. Pour ce cas particulier, cet algorithme porte maintenant le nom d'algorithme d'Euclide[Note 5]. Il existe aussi une démonstration différente, encore présente chez Euclide, et citée par Aristote « Ils prouvent que le diamètre du carré est incommensurable au côté en montrant que, si l'on admet qu'il lui est commensurable, un nombre impair serait égal à un pair[28]. » L'historien Oskar Becker montre que ce raisonnement[29] est fondé sur un savoir archaïque[Note 6] des Grecs en matière d'arithmétique géométrique, elle est peut-être très ancienne. La méthode consiste à démontrer que « Le double d'un nombre carré n'est jamais un nombre carré ».
Une reconstitution de la possible démonstration archaïque, à base arithmétique géométrique, s'appuie sur la figure de gauche. Elle procède encore par l'absurde. On considère le plus petit nombre carré de côté a somme de deux nombres carrés de côté b. Le nombre carré de côté a est pair et donc a l'est aussi[Note 7]. Le côté b est impair, sinon, en choisissant une unité deux fois plus grande on trouverait une nouvelle valeur deux fois plus petite que a, dont le carré est la somme de deux carrés. Par ailleurs, un carré de côté b possède la même aire qu'un rectangle de hauteur a et deux fois plus grande que sa base (en bleu sur la figure). Un tel rectangle est composé de deux nombres carrés, il est donc pair et le carré de côté b l'est aussi, ainsi que b. Le côté b est un nombre à la fois pair et impair. Cette contradiction montre que b n'existe pas et termine la démonstration.
Une fois cette proposition démontrée, l'irrationalité de la racine carrée de deux s'obtient en appliquant le théorème de Pythagore à la figure de droite. S'il existait une unité telle que tous les côtés du triangle rectangle isocèle de la figure soient des nombres entiers, le résultat précédent serait faux.
Conséquence
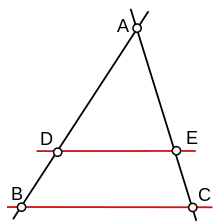
Une conséquence de l'existence d'irrationnels est que les démonstrations des propriétés établies sur les fractions d'entiers en début d'article ne traitent pas le cas général. Cependant, l'usage de l'algèbre géométrique et une approche différente permet encore de démontrer qu'une fraction b/c est égale à (a.b)/(a.c) si a, b, c sont trois nombres réels positifs tels que a et c soient non nuls.
Pour montrer ce résultat, on considère deux droites (noires sur la figure de droite) ayant comme intersection un unique point A. On définit les points B et C tels que la distance AB soit égale à b et AC à c. Les points B et C sont chacun sur une des droites, comme indiqué sur la figure. Le point D (resp. E) se situe sur la droite AB (resp. AC) et la distance AD (resp. AE) est égale à a.b (resp. a.c). Le théorème de Thalès indique que les droites rouges sont parallèles et que :
On peut ré-établir de la sorte toutes les lois régissant les quatre opérations sur les nombres quelconques. Ce travail est réalisé dans le livre VI des Éléments d'Euclide, qui pour cette raison est considéré comme de l'algèbre géométrique[30].
Toutes les démonstrations proposées dans cet article utilisent le principe de la mesure d'une ou de plusieurs aires. Cette règle est une caractéristique de l'algèbre géométrique[2] et cette démonstration n'est pas une exception. La démonstration d'Euclide du théorème de Thalès se fonde sur le même principe[Note 8].
Si les démonstrations ou illustrations précédentes sont toujours employées, de par leur simplicité et leur aspect intuitif, une construction rigoureuse des règles opératoires en algèbre, comme réalisée dans le livre VI, ne deviennent ni simples ni intuitifs.
Histoire des sciences
Difficultés
Les concepts mathématiques grecs ne sont pas adaptés à un langage algébrique. Cette remarque est particulièrement vraie pour les périodes précoces, comme celle pythagoricienne. Un nombre est une collection de plusieurs unités (un n'est pas un nombre), il correspond chez nous à un entier positif strictement supérieur à un. Un ratio n'est pas un nombre, mais une comparaison de deux grandeurs. La notion de ratio prend un sens à l'aide de la proportion. Quatre grandeurs a, b, c et d sont en proportion si le ratio a:b est égal au ratio c:d[31]. L'unité est une grandeur physique élémentaire, comme une longueur ou une aire qui, associée à des nombres ou des ratios, permet d'exprimer les grandeurs présentes dans une figure géométrique[32]. Dans les mathématiques hellénistiques, il n'existe pas véritablement de multiplication interne[33]. La multiplication de deux longueurs donne l'aire d'une figure plane, la multiplication de deux nombres a et b correspond plus à l'addition itérée a fois du nombre b qu'à une véritable multiplication. La différence entre leurs concepts et notre formalisme complexifie la compréhension des mathématiques grecques. En conséquence, la présentation des idées mathématiques contenues dans cet article est, pour des raisons de simplicité de compréhension, fort loin d'un véritable traité d'époque, comme on le trouve chez Euclide de Mégare. Par exemple, l'usage du symbole 1 dans la détermination de la section d'extrême et moyenne raison ne ferait pas sens pour un Grec.
La deuxième difficulté provient de la rareté des sources avant Platon. Les Ve et IVe siècles av. J.-C. sont presque vides en termes de traités mathématiques. Le savoir des historiens provient de sources postérieures de plusieurs siècles et pas toujours fiables[34], d'études précises sur la signification exacte de certains mots, que l'on retrouve aussi dans des textes non mathématiques[35], d'analyses archéologiques[36] ou encore d'étude des importations d'autres civilisations[37]. À l'aide de ces différentes indications, les historiens reconstruisent les démonstrations possibles et les placent dans leurs époques et leurs écoles respectives. Si, au fil du temps, l'ensemble des indices finit par donner une image cohérente et consensuelle dans les grandes lignes, de nombreux points de divergences, même sur des questions importantes, sont encore présents entre les différents spécialistes.
Usages du terme
Dans son livre de 1902, Zeuthen présente le concept d'algèbre géométrique essentiellement pour décrire le livre II d'Euclide et remarquer qu'il est équivalent à la résolution d'une équation quadratique. Il ne prend pas particulièrement de précautions oratoires ; il prête à Euclide la volonté de : « transporter, aux équations numériquement données, la solution générale trouvée pour les équations quadratiques[38] ». Tannery est convaincu de la véracité des témoignages, nombreux même si souvent tardifs et peu fiables, attribuant la découverte des irrationnels à l'époque de Pythagore[Note 9]. Il pense que ce véritable scandale logique[39] est à l'origine du miracle mathématique grec que sont les Éléments d'Euclide. Or, cette découverte ne peut avoir lieu que dans la mesure où la maîtrise des questions du second degré est suffisante. Ces questions relevant du domaine algébrique, le concept de Zeuthen lui semble fécond, et il l'adopte dès l'année suivante[40]. Pour Tannery, ce qui a limité les Grecs dans la démarche n'est pas tant l'absence d'une pensée algébrique qu'un vocabulaire adapté, qu'ils ne possédaient pas : « Ce qui manque aux mathématiciens grecs, ce sont moins les méthodes […] que les formules propres à l'exposition des méthodes[41] ».
Si, à l'image de Heath[42], cette idée est souvent adoptée par les historiens de l'époque, elle suscite une première polémique dans les années 1920[43]. La forme des mathématiques grecques est géométrique, en extraire une finalité algébrique n'est pas du goût de tous et Jacob Klein s'exprime ainsi : « De plus, la plupart des histoires classiques tentent d'appréhender les mathématiques grecques à l'aide du symbolisme moderne, comme si ce dernier était extrinsèque au contenu mathématique, qui pourrait être habillé sous n'importe quelle forme[44]. ». Parler d'équations chez Euclide, comme le fait Zeuthen, laisse penser que les Grecs disposaient déjà d'une inconnue sur lequel ils pouvaient opérer algébriquement, à l'image d'Al-Khawarizmi[Note 10]. Or, une telle démarche n'existe pas avant Diophante[45].
Otto Neugebauer apporte, dans les années 1940, des arguments en faveur de la thèse de Zeuthen et Tannery. Ses études sur d'autres cultures mathématiques montrent que les Grecs de l'époque de Pythagore ont importé des techniques mésopotamiennes[46]. Ce savoir se fonde sur des méthodes et des procédures de calcul (appartenant à la même famille que les fractions continues) permettant d'approximer des racines ou encore des méthodes de résolution de questions du second degré. Cette culture est algébrique, au sens où elle se fonde sur des équivalents d'algorithmes (le mot sera inventé plus tard) dont l'objectif est calculatoire. À l'image de la construction de la section d'extrême et de moyenne raison, de nombreux travaux de l'école de Pythagore sont des traductions de résultats mésopotamiens dans le langage géométrique ionien. Le concept d'algèbre géométrique s'étend à cette branche de savoir, maintenant couverte par l'algèbre et qui se démontre chez les Grecs à l'aide de la mesure des aires[47]. On y trouve la théorie des proportions, présente dans les livres V et VI qui décrivent des résultats maintenant contenus dans les axiomes d'un corps commutatif, des méthodes de résolution et d'analyse de la nature d'une solution d'une question de degré 2 présentes dans le livre II, ou encore l'application de l'algorithme d'Euclide à des proportions, dans le livre X, pour démontrer leur incommensurabilité. Elle contient aussi des démonstrations, déjà archaïques à l'époque d'Euclide, comme la théorie du pair et de l'impair.
Jusque dans les années 1970, les historiens n'hésitent plus à s'appuyer sur le concept de Zeuthen et Tannery, même si certains comme Wilbur Knorr[48] utilisent des précautions oratoires. La polémique est alors relancée. Sabetai Unguru (de)[49] remarque l'existence d'un schéma ordinaire, présent chez les Chinois, les Indiens, les Arabes ou encore les Européens, qui démarrent tous par de la géométrie pour atteindre, après un certain degré d'abstraction, une formalisation plus algébrique. Le schéma chez les Grecs serait alors inverse; à partir d'une conception d'orientation algébrique, héritée des Mésopotamiens, ils se seraient dirigés vers un système géométrique. Unguru n'imagine pas ce schéma réaliste. Cette position, qui imposerait selon lui une réécriture profonde de l'histoire des mathématiques grecques, est suivie par d'autres historiens comme Szabó[50].
La réplique est fournie par plusieurs spécialistes dont van der Waerden[51] qui estime que Szabó attache une importance trop forte au formalisme, que le propre des méthodes pythagoriciennes exposées ici est leur nature calculatoire et algorithmique et qu'elles sont bien héritées des Babyloniens. Michael Sean Mahoney[52], qui partage l'opinion de van der Waerden, remarque que les mathématiciens fondateurs de l'algèbre, comme Al-Khawarizmi ou Viète, s'inspirent largement des textes d'Euclide pour bâtir leurs théories.
Malgré la polémique, de nombreux spécialistes comme Burkert[53], Itard[47] ou Caveing[54] font usage du concept. Si des historiens généralistes l'utilisent aussi pour des ouvrages de vulgarisation, l'expression est souvent attachée à une mise en garde comme : « Le terme d'algèbre pour une époque où la recherche de l'inconnue n'est pas encore explicite, et encore moins l'étude des "équations", doit être utilisé avec prudence[55] ». L'usage du terme d'algèbre pour des mathématiques anciennes n'est pas tombé en désuétude[56]. Si l'usage de l'expression algèbre géométrique dépasse parfois en histoire des sciences le contexte grec[57], le cas est suffisamment rare pour mériter d'être noté.
Héritage

Si l'histoire de l'algèbre géométrique commence avec Pythagore, comme l'indique Maurice Caveing : « il y a des raisons de penser que la mathématique grecque n'est pas née, comme la fille de Métis, tout armée de la tête de Zeus[58] ». Pour cet auteur, l'école pythagoricienne hérite à la fois de l'école ionienne avec les travaux de Thalès de Milet et du patrimoine égyptien et mésopotamien. Les travaux de l'école de Thalès modifient déjà l'orientation des mathématiques grecques. Elle introduit la notion de preuve. Elles n'étaient surement pas aussi sophistiquées que celles que l'on trouve chez Euclide, cependant cette spécificité grecque est déjà présente, les différenciant de leurs prédécesseurs. Une deuxième spécificité des mathématiques ioniennes est son inclinaison à la géométrie. Les résultats prêtés à cette école sont, par exemple, le fait qu'un triangle isocèle possède deux angles égaux ou qu'un triangle de base le diamètre d'un cercle et dont le dernier sommet est situé sur le cercle est rectangle[59].
À la différence des Ioniens, la culture mésopotamienne est, à défaut d'être qualifiée d'algébrique, algorithmique[Note 11]. Les différentes tablettes qui nous sont parvenues montrent une mathématique sous forme de problèmes à résoudre. Celle notée BM 13901, qui contient 24 questions du second degré, laisse penser à une aide géométrique pour guider dans l'algorithme utilisé[60]. La tablette YBC 7289 montre la connaissance du résultat de l'algorithme décrit dans cet article pour la découverte de l'irrationalité de la section d'extrême et de moyenne raison, mais cette fois-ci appliqué à la diagonale d'un carré[61]. Tous les ingrédients pour découvrir l'irrationalité sont présents.
École pythagoricienne
L'école pythagoricienne cultive le culte du secret, à propos de son savoir. Il est donc difficile d'en connaître exactement la teneur, de dater précisément et d'associer un nom aux différents progrès. C'est néanmoins à cette école que l'on doit la naissance de l'algèbre géométrique grecque. Cette école hérite du savoir babylonien[46], ainsi que de l'orientation vers la géométrie et les démonstrations des Ioniens. Cette fusion des savoirs apporte un résultat nouveau : l'algèbre géométrique qui, à cette époque, se limite encore largement à de l'arithmétique géométrique.
.jpg.webp)
La science mésopotamienne apporte la puissance du calcul. Elle permet en géométrie un progrès que n'avaient probablement jamais réalisé les Égyptiens ou les Mésopotamiens. Un exemple est donné par les premières démonstrations partielles du théorème de Pythagore, que l'on attribue généralement à cette époque[62]. Elle ne s'applique que dans le cas où les côtés sont commensurables — c'est-à-dire où le triangle correspond à triplet pythagoricien — et utilise un quadrillage typique de l'arithmétique géométrique, illustré sur la figure de gauche. Dans cet exemple on cherche à trouver l'aire du carré en divers bleus, de côté l'hypoténuse d'un triangle rectangle, dont les autres côtés sont de longueurs 3 et 4. Le regroupement deux à deux des triangles intérieurs au carré bleu permet de conclure[63].
La puissance de la démarche les amène à l'appliquer dans des cas de longueurs incommensurables, sans nécessairement avoir conscience d'une possible incommensurabilité. La construction du pentagone impose la détermination de la section d'extrême et de moyenne raison, qui correspond à une question du deuxième degré. Les procédures calculatoires mésopotamiennes sont à même de venir à bout de cette difficulté. Cette construction est probablement réalisée à l'époque de Pythagore. Elle illustre l'orientation grecque, le résultat n'est pas une fraction approchant la valeur recherchée, mais une construction géométrique exacte[13].
La plus importante découverte souvent attribuée aux pythagoriciens et à l'algèbre géométrique est celle des incommensurables[Note 12]. Les éléments étaient déjà presque présents chez les Babyloniens, qui pourtant n'en ont jamais parlé. C'est probablement une attitude plus spéculative et moins pragmatique chez les Grecs qui fait la différence. Les Mésopotamiens concevaient néanmoins aussi les mathématiques comme une spéculation, comme le montre la tablette illustrée au paragraphe précédent. Elle donne la racine de deux avec une précision de cinq décimales, ce qui n'a aucun intérêt pratique au vu de leur technologie. Cependant les Mésopotamiens ont choisi une numération à notation positionnelle, un peu à l'image de notre notation décimale. Si cette notation est plus pratique pour les sciences de l'ingénieur, elle est moins adaptée que l'écriture fractionnaire des Grecs pour un travail théorique sur l'irrationalité. Une valeur dont la notation positionnelle ne se termine pas, comme 0,11111..., ne signifie en rien un caractère irrationnel[64].
De Pythagore à Euclide
L'école de Pythagore fournit un savoir encore loin de celui que l'on trouve, en matière d'algèbre géométrique, dans les Éléments d'Euclide. Pour atteindre ce but, on peut ranger les difficultés en trois catégories.
La première série de difficultés est d'ordre logique. La découverte des irrationnels montre l'existence de suites dont le comportement ne semble faire guère de sens. Celle donnée en exemple dans l'article n'est pas la plus étudiée, les Grecs lui préfèrent celle associée à la diagonale du carré. Elle s'obtient par un processus plus simple[65] et dispose des mêmes propriétés. Cette suite de proportions semble difficilement compatible avec l'hypothèse que tout couple de longueurs est commensurable. Si elle s'approche de plus en plus de la proportion recherchée, elle ne l'atteint jamais. Beaucoup ont vu dans le Paradoxe d'Achille et de la tortue une étude logique issue d'une réflexion sur les suites issues du calcul des incommensurables, c'est-à-dire une suite qui s'approche infiniment de sa cible, sans jamais la toucher[66]. L'absence de fondement logique suffisant aurait conduit Zénon d'Élée à condamner le raisonnement pythagoricien. Pour trancher de manière fiable ce scandale logique, pour reprendre l'expression de Tannery, il a fallu bâtir une logique consistante. À l'époque d'Aristote, le travail était fait. Ses Analytiques exposent clairement comment articuler un raisonnement par l'absurde sans risque d'erreur. Cet auteur utilise plusieurs fois l'exemple du fait que la diagonale d'un carré n'est pas commensurable avec son côté[28].
La deuxième série de difficultés concerne la modification du cadre conceptuel, imposée par les incommensurables. À l'époque de Pythagore, le théorème qui porte son nom est une égalité entre des nombres — toujours entiers chez les Grecs —; chez Euclide, ce théorème est une égalité entre des aires, qui n'ont cette fois-ci aucune raison de pouvoir être représentés par des nombres[67]. Cette modification impose une reconstruction totale de la mathématique, la démonstration du théorème de Thalès doit aussi être revue ainsi que toutes les démonstrations qui doivent maintenant quitter leur gangue commensurable et ne peuvent plus s'appuyer sur une logique fondée sur l'arithmétique géométrique. Maîtriser les incommensurables suppose aussi une arithmétique plus forte, pour mener à bien le raisonnement présenté pour la découverte des irrationnels. Chez Euclide, le raisonnement qui montre que dans le cas de grandeurs commensurables l'algorithme s'arrête, est devenu rigoureux. Il a néanmoins quitté son origine d'arithmétique géométrique, cet algorithme ne fournit plus l'unité de la figure (c'est-à-dire la plus grande unité qui permet d'exprimer les deux longueurs comme des multiples de l'unité) mais le plus grand commun diviseur entre deux nombres. L'historien Jean Itard s'exprime ainsi à propos de la théorie des nombres chez Euclide : « Elle est à peu près totalement dégagée de l'arithmo-géométrie, de la numération pratique et de la logistique, mais reste étroitement liée à la théorie des rapports[68] ».
Enfin, la troisième série de difficultés consiste à développer les outils permettant de comprendre le comportement asymptotique de l'étrange suite des origines de la découverte. D'une manière ou d'une autre, elle impose une certaine maîtrise du phénomène de limite, qui est alors traitée par l'exhaustion. Le livre V des Éléments permet de construire un univers admettant les incommensurables et les phénomènes de convergence, tout en conservant les propriétés algébriques exprimées maintenant sous forme d'axiomes comme la distributivité de la multiplication par rapport à l'addition dans le corps des réels[69]. Ce travail n'est pas sans conséquences, il impose ce qui deviendra l'axiome d'Archimède et permettra de fonder solidement l'argument de la descente infinie[70].
L'algèbre géométrique chez Euclide
Deux siècles séparent Pythagore et Euclide. À certains égards, la finalité n'a pas évolué. On y trouve toujours les méthodes prouvant les propriétés algébriques des proportions, comme la distributivité présente dans les livres V et VI, les procédures de résolution de questions du second degré et l'usage de l'anthyphérèse — équivalent à une fraction continue — au livre X pour établir l'incommensurabilité de certaines proportions. À d'autres égards, la théorie est métamorphosée. Elle s'appuie sur une logique axiomatisée[Note 13], la théorie des proportions prend en compte les incommensurables et l'arithmétique utilisée n'a plus grand chose à voir avec celle de Pythagore. En conséquence, toutes les pistes de démonstrations présentées dans cet article sont explorées rigoureusement avec succès et les paradoxes n'en sont plus. Si l'arithmétique géométrique de Pythagore découvre les incommensurables, l'algèbre géométrique d'Euclide les maîtrise. Le grand absent reste le nombre qui se limite encore aux entiers. Eudoxe ne peut pas définir l'axiome d'Archimède, tel que nous l'imaginons aujourd'hui. Cet axiome dépend de la grandeur considérée et le mathématicien ne traite finalement que le cas des aires[70]
Si les fondamentaux introduits à l'époque de Pythagore restent empreints de l'origine mésopotamienne, la finalité est modifiée. Un algorithme comme l'anthyphérèse ne sert plus à approximer une proportion, mais à établir la propriété d'incommensurabilité. Le mépris des calculs pour les Grecs est notoire, Hérodote est arrêté par une division par 48[71]. Pour Szabó, cette modification de finalité n'est pas le plus important. Il n'existe aucun formalisme algébrique chez les Grecs et le fait que l'objet principal d'étude soit une proportion et non pas un nombre n'est guère un facteur favorable. Cette absence de formalisme algébrique est la preuve d'une orientation géométrique, loin des préoccupations et des idées d'un précurseur en algèbre comme Diophante. Chez Euclide, l'idée d'équation n'apparaît pas et ne peut apparaître. Opérer sur une inconnue et non plus uniquement des nombres, n'est ici guère envisageable[72]. Pourtant, l'équation et son inconnue sont souvent considérées comme l'acte de naissance de l'algèbre[50].
Pour van der Waerden, le propre de l'algèbre est la mise en évidence et l'usage d'une structure. Le travail d'Eudoxe consiste à assurer l'existence d'un monde aux propriétés algébriques, comme la distributivité ou la commutativité d'une multiplication de proportions, tout en respectant une relation d'ordre. Cette question est fondamentalement algébrique et le fait qu'Eudoxe trouve un résultat équivalent aux coupures de Dedekind[73] n'est pas le fruit du hasard, ils cherchent tous deux à résoudre la même question, indépendamment du vêtement ou du formalisme choisi et la matière mathématique reste la même. De même, Le livre II établit les propriétés couramment appelées identités remarquables. Elles sont valables dans tous les anneaux commutatifs et donc celui des proportions géométriques des Grecs[Note 14] Le fait de travailler dans une structure à vocation géométrique ne modifie en rien leur nature algébrique. L'usage chez les Grecs de l'anthyphérèse a pour objectif une classification des incommensurables. Cette idée, qui sera poussée beaucoup plus loin dans la théorie de Galois, est aussi une question algébrique. En conclusion et pour van der Waerden, si la finalité et le formalisme sont géométriques, la nature même de l'algèbre géométrique reste inchangée depuis la Mésopotamie[51].
Pour les fondateurs de l'algèbre arabe et européenne, l'algèbre géométrique s'avère indispensable. La logique de la résolution d'une équation par Al-Khawarizmi n'est possible que dans la mesure où les propriétés algébriques de l'ensemble dont sont issus les coefficients du polynôme sont établies. Dans son traité Abrégé du calcul par la restauration et la comparaison, Al-Khawarizmi s'appuie sur Euclide pour établir la pertinence de la démarche, tout comme son disciple Abu Kamil[74]. Le livre V est le seul à proposer une construction algébrique suffisamment solide pour représenter la structure des nombres réels positifs. Euclide, ne disposant pas de manière pour exprimer les incommensurables, développe dans un langage géométrique un équivalent des identités remarquables — au sens de van der Waerden — de manière générique. Cette généricité est indispensable pour les premiers algébristes arabes qui ne disposent pas de paramètre et doivent se contenter d'illustrer leurs principes sur des exemples. Au XVIe siècle en Europe, Viète comble cette lacune et développe le concept du paramètre, généralisant l'algèbre et autorisant l'expression de résultats plus puissants, comme les relations entre coefficients et racines[75]. Pour Viète, la construction de l'algèbre géométrique reste indispensable[76]. Ainsi, pendant près de 2000 ans, l'algèbre géométrique est un outil incontournable pour les algébristes européens et arabes. Cet élément convainc Mahoney du caractère algébrique de la théorie[52].
Annexes
Bibliographie
- Hieronymus Georg Zeuthen, Histoire des mathématiques dans l'antiquité et le moyen âge, Gauthier-Villars, (lire en ligne)Zeuthen lance le concept d'algèbre géométrique dans cette référence. Vis-à-vis d'une conception contemporaine de l'histoire des sciences, il est daté. Il prête par exemple aux Grecs la capacité de résoudre des équations, ce que les spécialistes de notre époque ne font plus.
- Paul Tannery, Notions de mathématiques, Paris, Delagrave, (lire en ligne)Tannery lance véritablement le concept en lui accordant un rôle et une importance historique.
- (en) Thomas Heath, The Thirteen Books of Euclid's Elements, Books 1 and 2, Cambridge, 1926L'édition des livres d'Euclide commentés par Heath est l'une des références sur le sujet.
- (en) Otto Neugebauer, The Exact Sciences in Antiquity, Dover, , 240 p. (ISBN 978-0-486-22332-2)Cette référence étudie l'influence des Mésopotamiens sur les Grecs.
- (en) Walter Burkert, Lore and Science in Ancient Pythagoreanism, Harvard University Press, , 535 p. (ISBN 978-0-674-53918-1, présentation en ligne)Ce livre est la référence principale utilisée dans l'article pour la période pythagoricienne.
- Euclide (trad. Bernard Vitrac), Les Éléments [détail des éditions] (1990-2001) (ISBN 978-2130432401)Ce livre est l'une des éditions française de référence sur Euclide. Aux pages 366-376 on trouve une description de la polémique autour du concept d'algèbre géométrique.
- Maurice Caveing, La figure et le nombre : recherches sur les premières mathématiques des Grecs, Éditions du Septentrion, 1998a, 424 p. (ISBN 978-2-85939-494-3, présentation en ligne)Ce traité d'histoire des mathématiques grecs de la période hellénistique fait fréquemment référence au concept de l'article.
- Maurice Caveing, L'irrationalité dans les mathématiques grecques jusqu'à Euclide, Éditions du Septentrion, 1998b, 343 p. (ISBN 978-2-85939-539-1)
- Árpád Szabó, L'aube des mathématiques grecques, Vrin, , 367 p. (ISBN 978-2-7116-1279-6, présentation en ligne)Árpád Szabó est l'un des contestataires du concept. Il explicite les raisons de son opinion dans un appendice de ce livre.
- (en) Bartel L. van der Waerden, Geometry and Algebra in Ancient Civilizations (1983, rééd. Springer 2002) réédition (ISBN 978-3540121596)Van der Waerden est à la fois un célèbre historien des mathématiques antiques, mais aussi un algébriste ayant résolu le quinzième problème de Hilbert.
Notes
- Une véritable lecture des textes mathématiques d'avant Euclide n'est pas aussi simple. Pour les Grecs, les nombres sont toujours des entiers. L'équivalent chez eux de nos nombres rationnels correspondent chez eux à ce qu'ils appellent un logo, qui n'est pas un nombre mais une proportion.
- Voir l'article Équation du second degré.
- Voir l'article Fraction continue.
- Les historiens n'ont pas déterminé si la découverte provient d'une analyse de la diagonale du carré ou celle du pentagone. Ils ont encore moins déterminé le raisonnement à l'origine de cette découverte. Caveing subodore que la première découverte a eu lieu sur la suite associée au raisonnement présenté dans ce paragraphe.
- La descente infinie est présentée dans l'article détaillé, la démonstration du caractère fini d'une fraction continue d'un nombre rationnel est démontré dans l'article Fraction continue.
- Une pièce écrite en -480 par Épicharme semble faire référence à une connaissance du principe du pair et de l'impair.
- Une démonstration, fondée sur l'arithmétique géométrique, est proposée au paragraphe sur les nombres carrés.
- La démonstration d'Euclide est proposée dans l'article détaillé.
- C'est souvent à Pythagore lui-même que les témoignages attribuent la découverte des irrationnels.
- Pour cette question, voir l'article Théorie des équations.
- Ce qui est encore un anachronisme car ce terme provient d'Al-Khawarizmi, un perse qui n'apparaît que plus de mille ans plus tard
- Si cette idée d'attribution aux pythagoriciens est partagée par Tannery, Zeuthen, Heath, Becker, Fritz, Szabó, Michel (it) ou Caveing, d'autres comme Neugebauer imaginent une découverte plus tardive et d'autres encore, comme Burkert, ne se prononcent pas.
- Ce n'est qu'au XIXe siècle que les failles de l'édifice logique seront mises en évidence.
- En toute rigueur, il faudrait ajouter les proportions négatives pour obtenir une structure d'anneau, ce que ne faisaient pas les Grecs.
Références
Références didactiques :
- Charles-E. Jean, « nombre figuré », sur récréomath.
- Cette présentation s’inspire de : Claudie Asselin-Missenard et André Deledicq, « Les carrés de 1 à 25 », Jeu tests & quiz mathématiques, Les éditions du Kangourou, 2010, p. 22.
- Cette présentation s’inspire de : Claudie Asselin-Missenard et André Deledicq, « Les carrés de Babylone », Jeu tests & quiz mathématiques, Les éditions du Kangourou, 2010, p. 24.
- Gérard Villemin, « Impairs, Carrés et Cubes », sur Nombres - Curiosités, théorie et usages.
Références universitaires :
- Cette citation est extraite du premier exemple d’usage de l’arithmétique géométrique de Zeuthen 1902, p. 31.
- « Parmi les diverses échappatoires tentées, et réussies, par les mathématiciens grecs […] se place la partie de « l'algèbre géométrique » (expression de Zeuthen) qu'est l'application des aires. » Paul-Henri Michel et Jean Itard, La science antique et médiévale, des origines à 1450, Quadrige, , p. 231-233.
- Paul Tannery Mémoires scientifiques, Paris-Toulouse, Privat, 1912, I, p. 268.
- Plus précisément, Zeuthen considère que l’arithmétique géométrique est une introduction à l’algèbre géométrique : Zeuthen 1902, p. 31.
- Zeuthen n’est pas l’unique historien des sciences à considérer que l’arithmétique géométrique est une branche de l’algèbre géométrique : Árpád Szabó (de) utilise ce terme pour décrire les résultats arithmétiques connus des Babyloniens et démontrés géométriquement par les Grecs, cf. (en) Árpád Szabó, The Beginnings of Greek Mathematics, Springer, , 358 p. (ISBN 978-90-277-0819-9, présentation en ligne), p. 31[Information douteuse] (traduit de (de) Anfänge der griechischen Mathematik, de Gruyter, (lire en ligne) ; version française : Les débuts des mathématiques grecques, J. Vrin, , 403 p. (ISBN 978-2-7116-0691-7) ; à ne pas confondre avec Szabó 2000).
- D’autres historiens utilisent le terme d’arithmo-géométrie pour désigner cette technique mathématique : Jean Itard, Les livres arithmétiques d'Euclide, Hermann, 1961, p. 77.
- Burkert 1972, p. 428.[Information douteuse]
- C'est le premier exemple d'arithmétique géométrique de Zeuthen 1902, p. 33.
- Pour plus de détails, voir : Christine Proust, « Le calcul sexagésimal en Mésopotamie », p. 20.
- De manière plus générale, les Pythagoriciens de -480 connaissaient probablement la « théorie du pair et de l'impair » et savaient déduire la parité d'un produit, connaissant la parité des facteurs : (de) O. Becker, « Die Lehre von Geraden und Ungeraden im neunten Buch der euklidischen Elemente », Quellen und Studien sur Geschichte der Mathematik, Astronomie und Physik, b, vol. 3, , p. 533-553[réf. à confirmer].
- Cette méthode est décrite dans Caveing 1998b, p. 91.
- Zeuthen 1902, p. 31.
- (en) Thomas Little Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, CUP, (1re éd. 1921), 468 p. (ISBN 978-1-108-06306-7, présentation en ligne), p. 160.
- Depuis l'origine, ces questions du second degré sont au cœur de l'algèbre géométrique : Zeuthen 1902, p. 42-43.
- Jean-Luc Périllié, Symmetria et rationalité harmonique : origine pythagoricienne de la notion grecque de symétrie, L'Harmattan, , 282 p. (ISBN 978-2-7475-8787-7), p. 144.
- DahanPeiffer, p. 74.
- Zeuthen 1902, p. 36-44.
- Elle est équivalente à celle de Zeuthen 1902, p. 39.
- Voir les explications dans DahanPeiffer, p. 60.
- Cette association entre l'algèbre géométrique et l'étude de l'irrationalité est fréquente. Walter Burkert indique « The conquest of the irrational in Greek mathematics, and along with it the development of « geometrical algebra » ... » : Burkert 1972, p. 465.
- Walter Burkert, un spécialiste de Pythagore et de son école, précise : « The only certainty about the discovery of irrationality is that Theodorus of Cyrene proved that √n (for n = 3, ... 17 and not a perfect square) is irrational. » dans Burkert 1972, p. 439[Information douteuse].
- L'objet de Caveing 1998b est de passer en revue ces différentes hypothèses.
- (en) Kurt von Fritz, « The Discovery of Incommensurability by Hippasus of Metapontum », Ann. of Math. (2), vol. 46, n° 2, 1945, p. 242-264 DOI:10.2307/1969021.
- La méthode est décrite dans Caveing 1998b, p. 99-119.
- Cet algorithme est décrit dans l'article : Benoît Rittaud, « À un mathématicien inconnu ! », sur Bibnum.
- Caveing 1998b, p. 117.
- Maurice Caveing, « À propos des débuts des mathématiques grecques. Réflexions sur l'ouvrage de A. Szabo », Revue d'histoire des sciences, vol 32, 1979, p. 168.
- Aristote, Analytiques postérieurs I, 23.
- Becker 1934.
- La référence suivante contient la citation : « On désigne sous le nom d’algèbre géométrique grecque, toute une série de problèmes qui figurent dans le livre deux et le livre six des Éléments d’Euclide, qui sont exprimés et résolus géométriquement […] » : Eliane Cousquer, « De la théorie des proportions à la théorie des nombres réels », Laboratoire LAMIA, 1995, p. 8.
- (en) Wilbur Richard Knorr, The Evolution of the Euclidean Elements : A Study of the Theory of Incommensurable Magnitudes and its Significance for Early Greek Geometry, Springer, , 374 p. (ISBN 978-90-277-0509-9), p. 15.
- Aristote, Métaphysique, 1052b, p. 20-28.
- « Signalons toutefois que la théorie grecque des rapports présente un point faible,à savoir que leur ensemble n'est muni que d'une structure de groupe et non pas d'une structure de corps. Ce groupe, il est vrai, est complété par quelques applications de l'ensemble sur lui-même, "inversion", "composition", "séparation", qui sont, au fond, les transformations de base de notre groupe modulaire. » Michel et Itard 1994, p. 231-233.
- Voir à ce sujet le paragraphe intitulé On the interpretation of sources : Knorr 1974, p. 5.
- Toute la partie I de cette référence est une glose sur le sens exact du mot grec dynamis, qui permet d'attribuer un rôle aux Éléates : Szabó 1978, p. 31.
- Ici, l'auteur reprend une vieille analyse de Heath pour évaluer le savoir d'Hippase sur le pentagone : Périllié 2005, p. 147.
- C'est ce que fait largement l'auteur dans son premier chapitre La percée des Ioniens : Caveing 1998a, p. 31-75.
- Zeuthen 1902, p. 43.
- Paul Tannery, Pour L'Histoire de La Science Hellène, BiblioBazaar, rééd. 2008 (ISBN 978-0559304156), p. 251.
- Tannery 1903, chap. II, § 189.
- Citation reprise de (en) Michael S. Mahoney, « Another look at Greek geometrical analysis », Arch. Hist. Exact Sci., vol. 5, , p. 18-348.
- Heath 2013, p. 153.
- Bernard Vitrac, Peut-on parler d'algèbre dans les mathématiques grecques anciennes ? CNRS, UMR 8567, Centre Louis Gernet, p. 3.
- Traduction libre de la citation : « Moreover, most of the standard histories attempt to grasp Greek mathematics itself with the aid of modern symbolism, as if the latter were an altogether external form which may be tailored to any desirable content. » Jacob Klein, Greek mathematical thought and the origin of algebra, Dover Publications (traduction de 1992 d'un livre de 1934) (ISBN 978-0486272894), p. 5.
- Luis Radford, « Diophante et l'algèbre pré-symbolique », Bulletin AMQ, (lire en ligne).
- Neugebauer 1969, p. 145-176.
- Michel et Itard 1994, p. 231-233.
- Knorr 1974, p. 11.
- (en) S. Unguru, « On the need to rewrite the history of Greek mathematics », Arch. Hist. Exact Sci., vol. 15, 1975, p. 67-114.
- L'appendice 3 de Szabó 2000 est entièrement consacré à ce concept.
- Bartel Leendert van der Waerden, « Defence of a "Shocking" Point of View », Arch. Hist. Exact Sci., vol. 15, n° 3, 1976, p. 199-210.
- Mahoney 1968.
- Burkert 1972, p. 463.
- On en trouve 11 occurrences dans Caveing 1998a, p. 19.
- DahanPeiffer, p. 77.
- Voir par exemple (en) Jens Høyrup, Lengths, Widths, Surfaces: A Portrait of Old Babylonian Algebra and Its Kin [détail de l’édition], p. 278.
- Adof P. Youschkevitch, « Les mathématiques arabes (VIIIè-XVè siècles) », Revue d'histoire des sciences, vol 30, 1977, p. 372.
- Caveing 1998a, p. 19.
- Caveing 1998a, p. 33-75.
- Christine Proust Mathématiques en Mésopotamie Site CultureMath (ENS Ulm - DESCO) (2006)
- Benoît Rittaud À un mathématicien inconnu ! Bibnum
- Aucune certitude n'existe sur la nature de la démonstration de l'époque de Pythagore, deux hypothèses sont émises et celle présentée ici est l'une des deux. Les deux hypothèses supposent néanmoins les côtés commensurables : Éliane Cousquer 'Le théorème de Pythagore'
- Caveing 1998b, p. 91.
- Les informations de ce paragraphe sur les pythagoriciens sont extraites de Burkert 1972, p. 428.
- Szabó 2000, p. 153.
- Cette idée est exprimée tout d'abord par Tannery, longuement développé par Szabó et est expliquée dans J.-L. Périllié, La découverte des incommensurables et le vertige de l'infini, transcription d’une conférence qui a eu lieu le 16 mai 2001 à Grenoble, p. 19-21.
- Un exposé est disponible sur le site : Éliane Cousquer 'Le théorème de Pythagore'
- Jean Itard, Les livres arithmétiques d'Euclide, Hermann, 1961, p. 77.
- L'analyse est proposée dans Jean-Louis Gardies, L'Héritage épistémologique d'Eudoxe de Cnide : un essai de reconstitution, Vrin, , 156 p. (ISBN 978-2-7116-0977-2), p. 67-79.
- L'analyse est proposée dans Gardies 2000, p. 79.
- Zeuthen 1902, p. 46.
- Voir à ce sujet Radford 1991.
- Jean-Louis Gardies, Eudoxe et Dedekind, Revue d'histoire des sciences, vol. 37, n° 37-2, 1984, p. 111-125.
- DahanPeiffer, p. 85-86.
- Elles sont exprimées pour la première fois par Jacques Peletier du Mans en 1554 : IREM de Rennes François Viète Chap 11.8 p. 164
- DahanPeiffer, p. 110.
Article connexe
Lien externe
(en) Luigi Borzacchini, « Geometric algebra », sur Dipartimento di Matematica, Università degli studi di Bari
- Portail de l’algèbre
- Portail de la géométrie