Équations de Barré de Saint-Venant

Les écoulements quasi-unidimensionnels, par exemple ceux des cours d'eau, sont décrits par les équations de Barré de Saint-Venant obtenues par Adhémar Barré de Saint-Venant en 1871[1] et précisées en 1888[2]^,[3].

Cinq gouttes tombent successivement dans l'angle d'un récipient à section carrée. En se propageant les ondes de gravité créées se réfléchissent sur les parois et interfèrent.

Propagation d'une onde de gravité sur un banc de sable sous marin de forme elliptique.

Par extension cette appellation a été étendue aux écoulements en eau peu profonde (en anglais shallow water) qui correspondent à des problèmes quasi-bidimensionnels. On les rencontre en géophysique par exemple pour décrire les courants de marée. À ces phénomènes sont associées des ondes (onde de Rossby, onde de Kelvin, onde de Poincaré, mascaret, tsunami) dont l'étude de certaines d'entre elles est antérieure à 1850[4].

Ces écoulements sont représentatifs de milieux non dispersifs. Dans le cas contraire le milieu est décrit par les équations de Boussinesq.

Écoulements en eau peu profonde

Schéma pour le système d'écoulement en eau peu profonde.

On désigne par s(x,y) l'altitude de la surface par rapport au géoïde, par b(x,y) la surface solide, par H = s - b la hauteur de fluide et g la pesanteur comptée négativement vers le bas.

Les équations des écoulements en eau peu profonde où l'on suppose la composante verticale w de la vitesse petite devant les composantes horizontales et celles-ci indépendantes de z s'écrivent

{\frac {\partial s}{\partial t}}+{\frac {\partial }{\partial x}}(Hu)+{\frac {\partial }{\partial y}}(Hv)=0\,,\;\;\;\;\;H=s-b

{\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}+g{\frac {\partial s}{\partial x}}=0

{\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}+g{\frac {\partial s}{\partial y}}=0

La pression est déduite de l'équilibre hydrostatique en chaque axe vertical.

Elles se généralisent aisément dans le cas où l'on souhaite prendre en compte la force de Coriolis[5] et plus difficilement si l'on souhaite prendre en compte les effets visqueux[6].

Démonstration

Équations de base

Les équations d'Euler s'écrivent

Équation d'incompressibilité pour le vecteur vitesse V = (u,v,w)

\mathbf {\nabla } \cdot \mathbf {V} =0

Équation de bilan de la quantité de mouvement

{\frac {D\mathbf {V} }{Dt}}={\frac {\partial \mathbf {V} }{\partial t}}+\mathbf {\nabla } \cdot \left(\mathbf {V} \mathbf {V} \right)=-{\frac {1}{\rho }}\mathbf {\nabla } p+\mathbf {g}

où ρ est la masse volumique constante, p la pression et g la gravité.

Conditions aux limites

Les altitudes sont comptées par rapport au géoïde.

Les conditions aux limites sont

sur le plancher z = -b(x,y) la vitesse est nulle

\mathbf {V} \cdot \nabla (z+b)=0=w+\mathbf {V} \cdot \nabla b

sur la surface z = s(x,y) la pression est la pression externe p₀ et la vitesse normale w est liée à s par

{\frac {Ds}{Dt}}={\frac {\partial s}{\partial t}}+\mathbf {V} \cdot \nabla s=w

Conservation de la masse

On introduit la hauteur d'eau H = s - b et les vitesses moyennes

{\overline {u}}={\frac {1}{H}}\int _{-b}^{s}u\mathrm {d} z\,,\;\;\;{\overline {v}}={\frac {1}{H}}\int _{-b}^{s}v\mathrm {d} z

En intégrant l'équation de continuité en z et en utilisant la règle de Leibniz on a

{\begin{array}{lcl}0&=&\int _{-b}^{s}\nabla \cdot \mathbf {V} \mathrm {d} z\\[0.6em]&=&\int _{-b}^{s}\left({\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}+{\frac {\partial w}{\partial z}}\right)\mathrm {d} z\\[0.6em]&=&{\frac {\partial }{\partial x}}\underbrace {\int _{-b}^{s}u\mathrm {d} z} _{H{\overline {u}}}+{\frac {\partial }{\partial y}}\underbrace {\int _{-b}^{s}v\mathrm {d} z} _{H{\overline {v}}}\underbrace {-\left.u\right|_{z=s}{\frac {\partial z}{\partial x}}-\left.v\right|_{z=s}{\frac {\partial z}{\partial y}}+\left.w\right|_{z=s}} _{w-\mathbf {V} \cdot \nabla s={\frac {\partial s}{\partial t}}={\frac {\partial H}{\partial t}}}-\underbrace {\left(\left.u\right|_{z=-b}{\frac {\partial b}{\partial x}}+\left.v\right|_{z=-b}{\frac {\partial b}{\partial y}}+\left.w\right|_{z=-b}\right)} _{w+\mathbf {V} \cdot \nabla b=0}\end{array}}

On obtient ainsi une nouvelle équation de conservation de la masse

{\frac {\partial H}{\partial t}}+{\frac {\partial }{\partial x}}(H{\overline {u}})+{\frac {\partial }{\partial y}}(H{\overline {v}})=0

Si de plus on suppose u et v indépendants de z cette équation devient

{\frac {\partial H}{\partial t}}+{\frac {\partial }{\partial x}}(Hu)+{\frac {\partial }{\partial y}}(Hv)=0

Conservation de la quantité de mouvement

Suivant la verticale

Par hypothèse, w est très petit devant u et v. La composante verticale de l'équation de quantité de mouvement s'écrit, en négligeant les dérivées de u en x et de v en y

{\frac {Dw}{Dt}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial z}}+g\,,\;\;\;\;\;g<0

En négligeant la dérivée lagrangienne de w l'équation de quantité de mouvement en z se réduit à l'équilibre hydrostatique

{\frac {\partial p}{\partial z}}=\rho g

dont la solution est immédiate (g est supposé constant sur la hauteur considérée)

p=\rho g(z-s)+p_{0}

d'où

{\frac {\partial p}{\partial x}}=-\rho g{\frac {\partial s}{\partial x}}\,,\;\;\;\;\;{\frac {\partial p}{\partial y}}=-\rho g{\frac {\partial s}{\partial y}}

Suivant l'horizontale

En négligeant les dérivées en z de u et v et en tenant compte des équations ci-dessus les composantes de l'équation de quantité de mouvement s'écrivent

{\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}+g{\frac {\partial s}{\partial x}}=0

{\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}+g{\frac {\partial s}{\partial y}}=0

Ce système est hyperbolique et, comme tel, admet des ondes caractéristiques nommées ondes de gravité. Celles-ci ont une vitesse que l'on déduit des valeurs propres

c={\sqrt {gH}}

Une simple analyse dimensionnelle suffit à confirmer cette valeur.

On peut obtenir une description de ces ondes en écrivant l'équation de conservation de la masse multipliée par g^½ et les équations de conservation linéarisées et multipliées par H^½. On suppose que la direction de propagation est x

{\frac {\partial }{\partial t}}(s{\sqrt {g}})+{\frac {\partial }{\partial x}}({\sqrt {H}}uc)=0

{\frac {\partial }{\partial t}}(u{\sqrt {H}})+c\,{\frac {\partial }{\partial x}}(s{\sqrt {H}})=0

Par substitution on obtient une équation d'onde

{\frac {\partial ^{2}}{\partial t^{2}}}(s{\sqrt {g}})={\frac {\partial }{\partial x}}\left(c^{2}\,{\frac {\partial }{\partial x}}\left(s{\sqrt {g}}\right)\right)

Cette équation décrit une onde de marée (en anglais tidal wave).

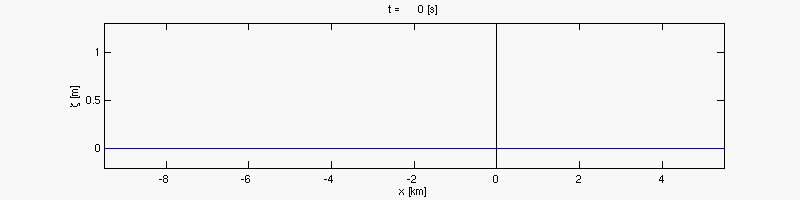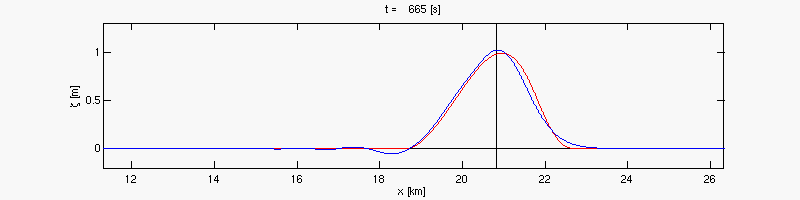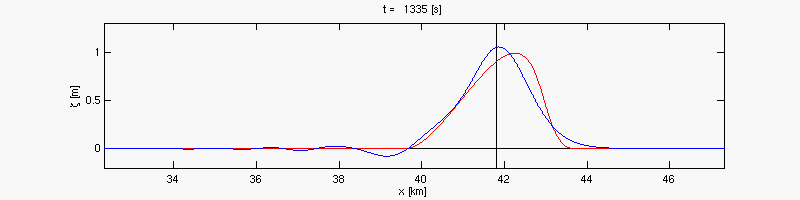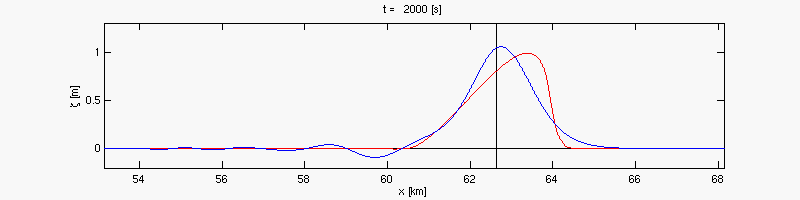
Génération et propagation d'une onde comme celle d'un tsunami. La courbe en bleu pour un milieu profond conduit à la formation d'un soliton. La courbe rouge est une onde non dispersive qui forme un front raide pouvant se décomposer en un paquet d'ondes de plus faibles longueurs d'onde. Pour celle-ci la profondeur d'eau dans le calcul est de 100 m.

Équations de Saint-Venant

Ces équations ont été décrites de manière heuristique et publiées par Saint-Venant en 1871. Elles décrivent l'écoulement quasi-unidimensionnel dans un canal ou un cours d'eau de largeur l(x). L'aire de la section droite de l'écoulement est A(x,t) et la vitesse moyenne de l'écoulement est U(x,t). La hauteur d'eau est h(y,t), compté à partir du fond z = 0. L'équation de conservation de la masse s'écrit

{\frac {\partial A}{\partial t}}+{\frac {\partial }{\partial x}}(AU)=0

L'équation de quantité de mouvement longitudinale s'écrit

{\frac {\partial }{\partial t}}(hU)+{\frac {\partial }{\partial x}}(hU^{2})+gh{\frac {\partial h}{\partial x}}={\frac {\tau _{x}}{\rho }}

τ_x(x,t) est le cisaillement appliqué au périmètre mouillé P(x,t).

L'équation en z est donnée par l'équilibre hydrostatique

{\frac {\partial p}{\partial z}}=\rho g

Ces équations peuvent être obtenues à partir des équations de Navier-Stokes.

Démonstration

Conservation de la masse

Comme montré dans l'encadré précédent la conservation en un point du canal est donnée par

{\frac {\partial h(y)}{\partial t}}+{\frac {\partial }{\partial x}}\int _{0}^{h(y)}u(y,z)\mathrm {d} z=0

En intégrant en y on obtient la relation souhaitée en remarquant que

A=\int _{0}^{l}h(y)\mathrm {d} y

et en définissant la vitesse moyenne

U={\frac {1}{A}}\int _{0}^{l}\int _{0}^{h}u(y,z)\mathrm {d} z\mathrm {d} y

Conservation de la quantité de mouvement

On part de l'équation shallow water avec viscosité[6] dans laquelle la vitesse moyenne transversale est nulle

{\frac {\partial }{\partial t}}(hU)+{\frac {\partial }{\partial x}}(hU^{2})+gh{\frac {\partial h}{\partial x}}={\frac {\tau _{x}}{\rho }}

où τ_x est le cisaillement sur la paroi.

On suppose que

$\scriptstyle {\frac {\partial h}{\partial x}}$ est indépendant de y (la pente en x est la même pour tous les points de la section droite)
τ_x est également indépendant de y

En intégrant en y, il vient

{\frac {\partial }{\partial t}}(AU)+{\frac {\partial }{\partial x}}(AU^{2})+gA{\frac {\partial h}{\partial x}}={\frac {P\tau _{x}}{\rho }}

On peut prendre en compte la pente α du terrain en remplaçant la gravité par sa composante en z et en introduisant la composante du poids en x

{\frac {\partial }{\partial t}}(hU)+{\frac {\partial }{\partial x}}(hU^{2})+gh\cos \alpha {\frac {\partial h}{\partial x}}=gh\sin \alpha -{\frac {\tau _{x}}{\rho }}

Évaluation du cisaillement

Cette évaluation se fait généralement en introduisant un coefficient de frottement C_f pour la couche limite sur le périmètre mouillé

\tau _{x}={\frac {1}{2}}C_{f}(h,U)\rho U^{2}

Ce coefficient représente la part du flux de quantité de mouvement transféré à la paroi. Sa forme résulte des lois de similitude[7] : lois de Chézy ou de Manning-Strickler

C_{f}(h)={\frac {2g}{K_{s}^{2}\,h^{\frac {1}{3}}}}

Le coefficient K résulte de l'expérience.

Références

Adhémar Jean Claude Barré de Saint-Venant, « Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et a l’introduction de marées dans leurs lits », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 73,‎ 1871, p. 147–154 et 237–240
M. de Saint-Venant, « Mémoire sur la prise en considération de la force centrifuge dans le calcul du mouvement des eaux courantes et sur la distinction des torrents et des rivières », Mémoires de l'Académie des sciences de l'Institut de France, vol. 44,‎ 1888, p. 245-273 (lire en ligne)
M. de Saint-Venant, « Mémoire sur la perte de force vive d'un fluide aux endroits où sa section d'écoulement augmente brusquement ou rapidement », Mémoires de l'Académie des sciences de l'Institut de France, vol. 44,‎ 1888, p. 193-243 (lire en ligne)
(en) Alex D. D. Craik, « The Origins of water Wave Theory », Annual Review of Fluid Mechanics, vol. 36,‎ 2004, p. 1-28 (lire en ligne)
(en) David A. Randall, « The Shallow Water Equations »
(en) Clint Dawson et Christopher M. Mirabito, « The Shallow Water Equations », 2008
Christophe Ancey (École Polytechnique Fédérale de Lausanne), Mécanique des fluides : Chapitre 2 : similitude (lire en ligne)

Ouvrages

(en) Hendrik C. Kuhlmann et Hans-Josef Rath (Eds.), Free Surface Flows, Springer-Verlag, 1998, 331 p. (ISBN 978-3-7091-2598-4, lire en ligne)
Olivier Thual, Des ondes et des fluides : articles pédagogiques multimédia, Toulouse, Cépaduès, 2005, 197 p. (ISBN 2-85428-655-3)
Olivier Thual, Hydrodynamique de l'environnement, Les éditions de l'École Polytechnique, 2010 (lire en ligne)
(en) Geoffrey K. Vallis, Atmospheric and Oceanic Fluid Dynamics, Cambridge University Press, 2017 (ISBN 978-1-107-58841-7)

Voir aussi

Portail de la physique
Portail des lacs et cours d’eau

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[Saint-Venant-1] Adhémar Jean Claude Barré de Saint-Venant, « Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et a l’introduction de marées dans leurs lits », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 73,‎ 1871, p. 147–154 et 237–240

[2] M. de Saint-Venant, « Mémoire sur la prise en considération de la force centrifuge dans le calcul du mouvement des eaux courantes et sur la distinction des torrents et des rivières », Mémoires de l'Académie des sciences de l'Institut de France, vol. 44,‎ 1888, p. 245-273 (lire en ligne)

[3] M. de Saint-Venant, « Mémoire sur la perte de force vive d'un fluide aux endroits où sa section d'écoulement augmente brusquement ou rapidement », Mémoires de l'Académie des sciences de l'Institut de France, vol. 44,‎ 1888, p. 193-243 (lire en ligne)

[4] (en) Alex D. D. Craik, « The Origins of water Wave Theory », Annual Review of Fluid Mechanics, vol. 36,‎ 2004, p. 1-28 (lire en ligne)

[5] (en) David A. Randall, « The Shallow Water Equations »

[Dawson-6] (en) Clint Dawson et Christopher M. Mirabito, « The Shallow Water Equations », 2008

[7] Christophe Ancey (École Polytechnique Fédérale de Lausanne), Mécanique des fluides : Chapitre 2 : similitude (lire en ligne)