Graphe d'états

Un graphe d'état est une suite d'états et de transitions réceptives. Pour ceux qui auraient une connaissance du GRAFCET on parle ici d'état et non d'étape. Les évolutions seront représentées par un jeton (et un seul) qui se déplace d'état en état.

États

Même si nous avons déjà rencontré la notion d'état, il est important de se rappeler :

Début d’un principe

Définition

Les états sont représentés comme d'habitude par des cercles et un identificateur qui est souvent un chiffre. Il existe parmi les états un état particulier, dit état initial qui est actif à la mise sous tension et représenté par un cercle double.

Fin du principe

Les états normaux (à gauche) initial (à droite)

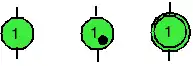
Voici des exemples d'états à droite.

Cette figure représente respectivement un état normal inactif, un état normal actif (on y ajoute un jeton), un état initial inactif (double cercle). Dire qu'on se trouve dans un état se représente donc par un jeton (comme pour les GRAFCETs).

Transitions

Une transition a toujours été décrite, jusqu'ici, au moyen d'une flèche et d'une éventuelle condition le passage d’un état à un autre : on parle de transition conditionnelle. Une telle transition ne spécifie pas ce qui se passe si la condition est fausse.

Une transition réceptive

Définition

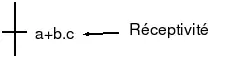
Une transition réceptive diffère d'une transition conditionnelle par un trait barrant la transition. Cette transition spécifie immédiatement ce qui se passe si la condition n’est pas vraie : on reste dans le même état.

Voici une transition réceptive (à droite)

La réceptivité est l'équation booléenne : c’est une valeur booléenne. La signification de cette transition peut être présentée par le dessin ci-contre.

Equivalence entre transition et transition réceptive

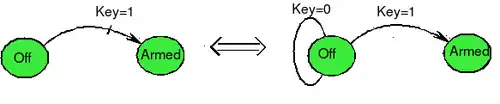
On aperçoit dans cette figure l’intérêt d'une transition réceptive : on retire les transitions d’un état sur lui-même. C’est tout mais c’est le genre de simplification qui peut simplifier grandement un dessin si l’on a plusieurs dizaines d'états.

Équations de récurrence

Du point de vue du codage des états, ce que l’on présente maintenant est souvent appelé Code One-hot. Cela signifie, en clair, qu'on utilise une équation de récurrence par état. Le graphe d'états présenté en figure plus loin possède quatre états, il sera donc décrit par quatre équations de récurrences. Comment trouver ces équations de récurrences ?

On cherche pour chacun des états i les conditions d'activations que l’on notera ${\displaystyle AC_{i}}$ et les désactivations que l’on notera ${\displaystyle D_{i}}$ puis on écrit une des deux équations ci-dessous suivant le type d'état que l’on a :

${\displaystyle {{x_{i}}^{+{}}}=AC_{i}+{\overline {D_{i}}}\cdot x_{i}+Init}$

pour un état initial et

${\displaystyle {{x_{i}}^{+{}}}=(AC_{i}+{\overline {D_{i}}}\cdot x_{i})\cdot {\overline {Init}}}$

pour un état normal. Init est une entrée ajoutée destinée à l'initialisation (synchrone ici).

Définition

• On appellera condition d'activation de l'état i et l’on notera ${\displaystyle AC_{i}}$ l'équation (combinatoire) qui permet de décrire comment on peut se retrouver dans cet état i au prochain front d'horloge, si l’on est pas dans l'état en question.
• On appellera condition de désactivation de l'état i et l’on notera ${\displaystyle D_{i}}$ l'équation combinatoire qui décrit les conditions qui vont faire qu'on va quitter l'état i au prochain front d'horloge en considérant qu'on est dans cet état.

Un exemple sera plus parlant qu'un long discours. Soit le graphe d'état ci-dessous :

Notre graphe d'états d'étude

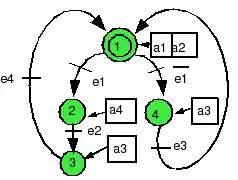
Cherchons les conditions d'activation ${\displaystyle AC_{i}}$ de chacun des états :

• ${\displaystyle AC_{1}=x_{3}\cdot e_{4}+x_{4}\cdot e_{3}}$
• ${\displaystyle AC_{2}=x_{1}\cdot e_{1}}$
• ${\displaystyle AC_{3}=x_{2}\cdot e_{2}}$
• ${\displaystyle AC_{4}=x_{1}\cdot {\overline {e_{1}}}}$

puis les conditions de désactivation

• ${\displaystyle D_{1}=e_{1}+{\overline {e_{1}}}=1}$
• ${\displaystyle D_{2}=e_{2}}$
• ${\displaystyle D_{3}=e_{4}}$
• ${\displaystyle D_{4}=e_{3}}$

Les équations de récurrence sont alors :

• ${\displaystyle {{x_{1}}^{+{}}}=AC_{1}+{\overline {D_{1}}}\cdot x_{1}+Init=x_{3}\cdot e_{4}+x_{4}\cdot e_{3}+Init}$
• ${\displaystyle {{x_{2}}^{+{}}}=(AC_{2}+{\overline {D_{2}}}\cdot x_{2})\cdot {\overline {Init}}=(x_{1}\cdot e_{1}+{\overline {e_{2}}}\cdot x_{2})\cdot {\overline {Init}}}$
• ${\displaystyle {{x_{3}}^{+{}}}=(AC_{3}+{\overline {D_{3}}}\cdot x_{3})\cdot {\overline {Init}}=(x_{2}\cdot e_{2}+{\overline {e_{4}}}\cdot x_{3})\cdot {\overline {Init}}}$
• ${\displaystyle {{x_{4}}^{+{}}}=(AC_{4}+{\overline {D_{4}}}\cdot x_{4})\cdot {\overline {Init}}=(x_{1}\cdot {\overline {e_{1}}}+{\overline {e_{3}}}\cdot x_{4})\cdot {\overline {Init}}}$

Équations de sorties

Nous n'avons encore jamais rencontré ce type d'équation.

Définition

On appellera équations de sorties, dans la suite de ce livre, toute équation permettant de lier les sorties physiques ou sorties véritables aux états internes. Je parle ici d'états internes car ils ne sont pas sensé être des sorties, même si cela arrive parfois. Les équations de sorties sont toujours combinatoires.

Les équations de sortie de l'exemple ci-dessus sont donc :

• ${\displaystyle a_{1}=x_{1}}$
• ${\displaystyle a_{2}=x_{1}}$
• ${\displaystyle a_{3}=x_{3}+x_{4}}$
• ${\displaystyle a_{4}=x_{2}}$

Implantation

On implante ces équations de récurrence facilement avec des bascules D (voir TD 3). Le schéma comporte deux parties : les équations de récurrences se retrouvent en partie gauche et les équations de sortie se retrouvent en partie droite.

N'oubliez jamais

Dans une équation de récurrence, l'état futur désigne toujours l'entrée d'une bascule D tandis que l'état présent désigne sa sortie. Faites attention, cette propriété n’est pas intuitive.

En suivant toutes ces règles, on trouve pour l'exemple ci-dessus le schéma donné maintenant :

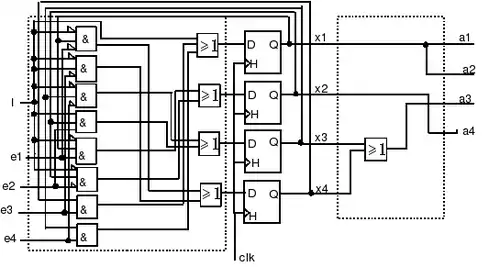
Essayez de retrouver les équations de récurrences sur ce schéma ainsi que les équations de sortie : ce travail n’est pas complètement inutile.

Posons-nous la question de savoir comment pourrait-on programmer une PAL à partir des équations.

Implantation en VHDL

Le programme VHDL est trouvé très facilement quand on a les équations : il suffit de les traduire en VHDL. Les équations de récurrences seront alors dans un "if clk'event ..." et du coup dans un process. Le process en question a une liste de sensibilité toute simple : l'horloge. Les équations de sorties ne seront pas dans ce process mes concourantes (à lui). Regardez tout cela das le programme ci-dessous :

-- programme VHDL correspondant au graphe d'états précédent
ENTITY graf1 IS 
PORT (I,e1,e2,e3,e4,clk : IN BIT;
      a1,a2,a3,a4 : OUT BIT);
END graf1;
ARCHITECTURE agraf1 OF graf1 IS
SIGNAL x1,x2,x3,x4,x5 : BIT;
BEGIN
  PROCESS(clk) BEGIN
    IF (clk'event AND clk='1') THEN
-- équations de récurrences
      x1 <= (x3 AND e4) OR (x4 AND e3) OR I;
      x2 <= (x1 AND e1 AND NOT I) OR (x2 AND NOT e2 AND NOT I);
      x3 <= (x2 AND e2 AND NOT I) OR (x3 AND NOT e4 AND NOT I);
      x4 <= (x1 AND NOT e1 AND NOT I) OR (x4 AND NOT e3 AND NOT I);
    END IF;
  END PROCESS;
--équations de sorties
  a1 <= x1;
  a2 <= x1;
  a3 <= x3 OR x4;
  a4 <= x2;
END agraf1;

Exercices