Soient ${\displaystyle f}$ et ${\displaystyle g}$ deux fonctions.

• Si ${\displaystyle \lim _{+\infty }f=+\infty }$ et ${\displaystyle g\geq f}$, alors ${\displaystyle \lim _{+\infty }g=+\infty }$.
• Si ${\displaystyle \lim _{+\infty }f=-\infty }$ et ${\displaystyle g\leq f}$, alors ${\displaystyle \lim _{+\infty }g=-\infty }$.

Soit ${\displaystyle a\in \mathbb {R} }$ ou ${\displaystyle a=+\infty }$ ou ${\displaystyle a=-\infty }$.

Si ${\displaystyle \lim _{a}f=L}$ et ${\displaystyle \lim _{a}h=L}$ et ${\displaystyle f\leq g\leq h}$, alors ${\displaystyle \lim _{a}g=L}$.

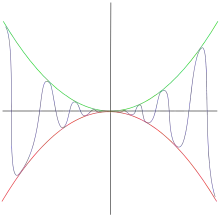
Soit ${\displaystyle \color {blue}g:x\mapsto x^{2}\sin \left({\frac {1}{x}}\right)}$. On cherche la limite de ${\displaystyle g}$ en 0.

Elle ne peut pas être déterminée par la propriété des limites

${\displaystyle \lim _{x\to a}(f(x)\cdot g(x))=\lim _{x\to a}f(x)\cdot \lim _{x\to a}g(x)}$,

parce que

${\displaystyle \lim _{x\to 0}\sin({\tfrac {1}{x}})}$

n'existe pas.

Mais en utilisant le théorème des gendarmes, il suffit de poser :

${\displaystyle \color {red}f:x\mapsto -x^{2}}$ ;

${\displaystyle \color {green}h:x\mapsto x^{2}}$.

Comme pour tout ${\displaystyle t\in \mathbb {R} ,~-1\leq \sin(t)\leq 1}$, on a pour tout ${\displaystyle x\in \mathbb {R} ^{*},~f(x)\leq g(x)\leq h(x)}$

Comme de plus ${\displaystyle \lim _{0}f=0}$ et ${\displaystyle \lim _{0}h=0}$, le théorème des gendarmes permet d'affirmer que ${\displaystyle \lim _{0}g}$ existe et est égale à ${\displaystyle 0}$.