Limites d'une fonction/Droites asymptotes

Définition qualitative

Définition

Soit ƒ une fonction dont la courbe représentative dans un repère est notée ${\mathcal {C}}$ .

Une droite ${\mathcal {D}}$ est dite asymptote à ${\mathcal {C}}$ lorsque ${\mathcal {C}}$ se rapproche infiniment de ${\mathcal {D}}$ .

On peut classer les asymptotes en trois « catégories » :

Les asymptotes horizontales
Les asymptotes verticales
Les asymptotes obliques

Asymptote horizontale

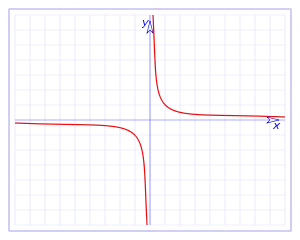
Prenons la fonction inverse. On sait que $\lim _{x\to +\infty }{\frac {1}{x}}=0$

Ceci montre que la courbe de la fonction inverse se rapproche de plus en plus de l’axe des abscisses, qui est la droite d'équation $y=0$ .

On dit alors que l'axe des abscisses est asymptote à la courbe de la fonction inverse en +∞.

De même, on a $\lim _{x\to -\infty }{\frac {1}{x}}=0$ , donc l’axe des abscisses est asymptote à la courbe de la fonction inverse en -∞.

Définition

Soit ƒ une fonction dont la courbe représentative dans un repère est notée ${\mathcal {C}}$ .

${\mathcal {C}}$ admet une asymptote horizontale d'équation y = L

en +∞ si $\lim _{x\to +\infty }f(x)=L$
en -∞ si $\lim _{x\to -\infty }f(x)=L$

Asymptote verticale

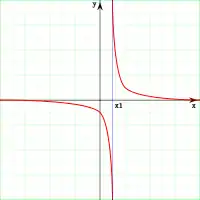
Prenons à présent la fonction $x\mapsto {\frac {1}{x-x_{1}}}$ , dont la courbe ${\mathcal {C}}$ est représentée ci-contre.

On a $\lim _{x\to x_{1}^{+}}{\frac {1}{x-x_{1}}}=+\infty$ et $\lim _{x\to x_{1}^{-}}{\frac {1}{x-x_{1}}}=-\infty$ .

On voit donc bien que ${\mathcal {C}}$ se rapproche de plus en plus de la droite verticale tracée en bleu lorsque x tend vers x₁. La droite en bleu a pour équation $x=x_{1}$

On dit que ${\mathcal {C}}$ a pour asymptote verticale la droite d'équation $x=x_{1}$ en x₁.

Définition

Soit ƒ une fonction dont la courbe représentative dans un repère est notée ${\mathcal {C}}$ .

${\mathcal {C}}$ admet une asymptote verticale d'équation x = a si la limite de ƒ en a est infinie.

Asymptote oblique

Exemple 1

Exemple

Soit ƒ la fonction définie sur $[0;+\infty [$ par : $f:x\mapsto {\frac {x^{2}+3}{x+1}}$

Déterminer le comportement de ƒ en $+\infty$
On note $E:x\mapsto f(x)-(x-1)$ . Pour tout $x\in \mathbb {R} ^{+}$ , donner l’expression de E(x).
Déterminer la limite de E(x) quand x tend vers plus l’infini.
Sur la calculatrice, tracer la courbe de ƒ et la droite d’équation y = x - 1. Que remarque-t-on ?

1. Déterminer le comportement de ƒ en $+\infty$

On factorise les termes de plus haut degré et on simplifie :

Pour tout

x\in [0;+\infty [,~f(x)=...

Or

\lim _{x\to +\infty }\cdots =\cdots

et

\lim _{x\to +\infty }\cdots =\cdots

Donc

\lim _{x\to +\infty }f(x)=...

Solution

1. Déterminer le comportement de ƒ en $+\infty$

On factorise les termes de plus haut degré et on simplifie :

Pour tout

x\in [0;+\infty [,~f(x)={\frac {x^{2}+3}{x+1}}={\frac {x^{2}\left(1+{\frac {3}{x^{2}}}\right)}{x\left(1+{\frac {1}{x}}\right)}}=x\cdot {\frac {1+{\frac {3}{x^{2}}}}{1+{\frac {1}{x}}}}

Or

\lim _{x\to +\infty }1+{\frac {3}{x^{2}}}=1

et

\lim _{x\to +\infty }1+{\frac {1}{x}}=1

Donc $\lim _{x\to +\infty }f(x)=+\infty$

2. On note $E:x\mapsto f(x)-(x-1)$ . Pour tout $x\in \mathbb {R} ^{+}$ , donner l’expression de E(x).

Soit

x\in \mathbb {R} ^{+}

$E(x)=\cdots$

Solution

2. On note $E:x\mapsto f(x)-(x-1)$ . Pour tout $x\in \mathbb {R} ^{+}$ , donner l’expression de E(x).

Soit

x\in \mathbb {R} ^{+}

${\begin{aligned}E(x)&={\frac {x^{2}+3}{x+1}}-(x-1)\\&={\frac {x^{2}+3}{x+1}}-{\frac {(x+1)(x-1)}{x+1}}\\&={\frac {x^{2}+3-(x^{2}-1)}{x+1}}\\&={\frac {4}{x+1}}\\\end{aligned}}$

Pour tout $x\in \mathbb {R} ^{+},~E(x)={\frac {4}{x+1}}$

3. Déterminer la limite de E(x) quand x tend vers plus l’infini.

$\lim _{x\to +\infty }\cdots =\cdots$

Donc

\lim _{x\to +\infty }E(x)=\cdots

Solution

3. Déterminer la limite de E(x) quand x tend vers plus l’infini.

$\lim _{x\to +\infty }x+1=+\infty$

Donc $\lim _{x\to +\infty }E(x)=0$

4. Sur la calculatrice, tracer la courbe de ƒ et la droite d’équation y = x - 1. Que remarque-t-on ?

Solution

4. Sur la calculatrice, tracer la courbe de ƒ et la droite d’équation y = x - 1. Que remarque-t-on ?

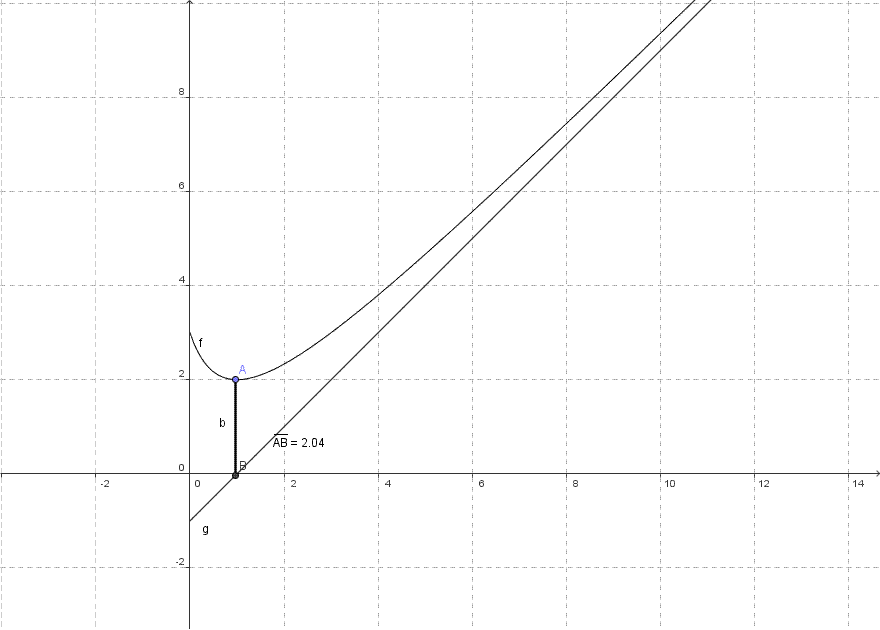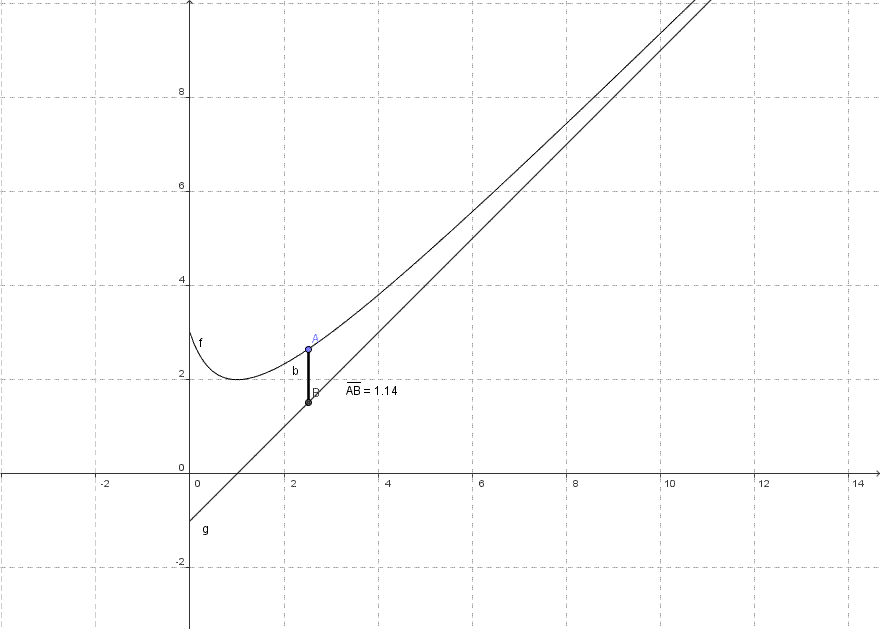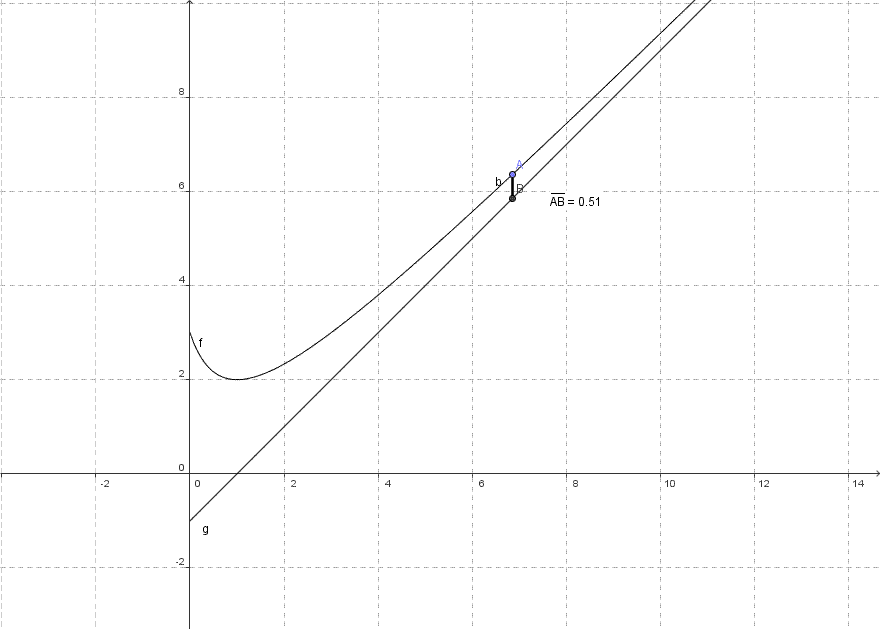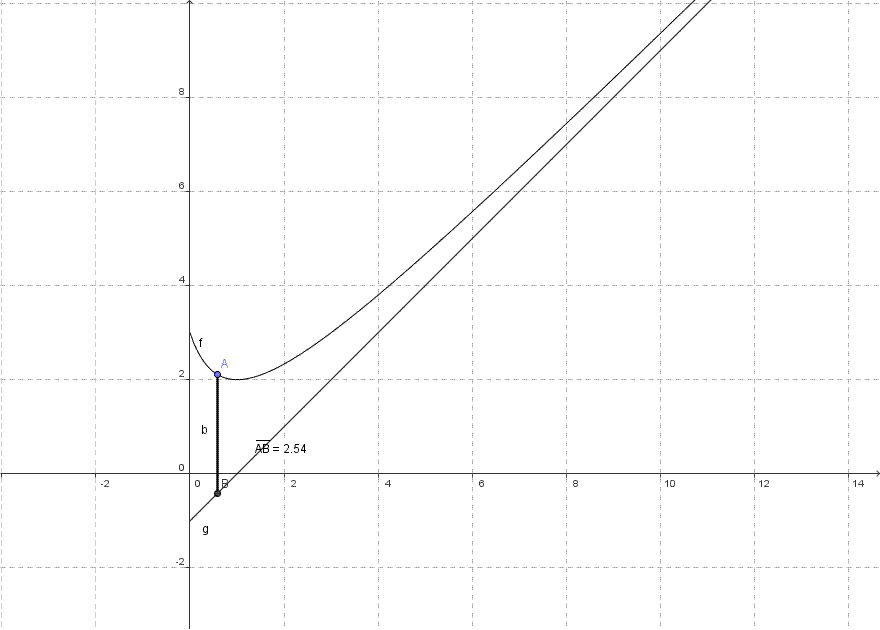
On remarque que l'écart entre la courbe de ƒ et la droite d'équation y = x - 1 se réduit quand x augmente. La courbe de ƒ semble ainsi se rapprocher de la droite sans jamais l'atteindre.

Théorème général sur les asymptotes obliques

Théorème

On pose pour tout $x,~E(x)=f(x)-(a.x+b)$

Si $\lim _{x\to +\infty }E(x)=0$ , alors la droite d’équation $y=a.x+b$ est asymptote à la courbe de ƒ.
Si de plus $a\neq 0$ , la droite d’équation $y=ax+b$ n’est pas horizontale et on parle d’asymptote oblique.

Dans l'exemple précédent, $E(x)=...$ et l'asymptote est ...

Définition

La quantité $E(x)=f(x)-(a.x+b)$ est appelée écart vertical algébrique entre la courbe et la droite.

Dans l'exemple précédent, $E(x)=...$ .

Propriété

Si $E(x)>0$ : la courbe est au-dessus de son asymptote.

Si $E(x)<0$ : la courbe est en dessous de son asymptote.

Dans l'exemple précédent :

${\begin{array}{c|ccc|}x&0&&+\infty \\\hline {\textrm {Signe~de}}~E(x)&&&\\\hline {\textrm {Position}}&&&\\\hline \end{array}}$

'Cas de l'exemple 1'

Notons ${\mathcal {C}}$ la courbe de ƒ et ${\mathcal {D}}$ la droite d'équation y = x - 1

Pour tout $x\in \mathbb {R} ^{+},~E(x)={\frac {4}{x+1}}$

${\begin{array}{c|ccccccc|}x&0&&+\infty \\\hline {\textrm {Signe~de}}~E(x)&&+&\\\hline {\textrm {Position}}&&{\mathcal {C}}{\textrm {~au-dessus~de~}}{\mathcal {D}}&\\\hline \end{array}}$

Exemple 2

Exemple

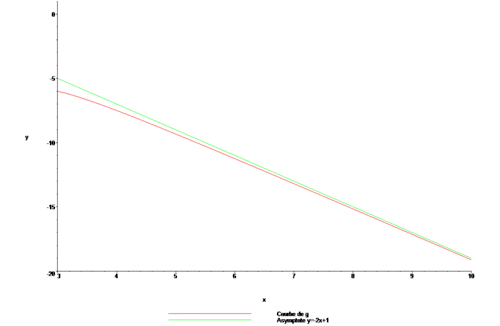
Soit g la fonction définie sur $I=[3;+\infty [$ par :

pour tout

x\in I,~g(x)={\frac {-2x^{2}+5x-3}{x-2}}

Déterminer le comportement de g en +∞
Trouver a et b tels que pour tout $x\in I,~g(x)=ax+b-{\frac {1}{x-2}}$
On pose pour tout $x\in I,~E(x)=g(x)-(ax+b)$ . Étudier le signe de E(x) et sa limite quand x tend vers plus l’infini.

1. Déterminer le comportement de g en +∞

On factorise par les termes de plus haut degré et on simplifie :

Pour tout

x\in I,~g(x)=\cdots

Or,

\lim _{x\to +\infty }\cdots =\cdots

et

\lim _{x\to +\infty }\cdots =\cdots

Donc

\lim _{x\to +\infty }f(x)=\cdots

2. Trouver a et b tels que pour tout $x\in I,~g(x)=ax+b-{\frac {1}{x-2}}$

${\begin{cases}a=\cdots \\b=\cdots \end{cases}}$

3. On pose pour tout $x\in I,~E(x)=g(x)-(ax+b)$ . Étudier le signe de E(x) et sa limite quand x tend vers plus l’infini.

Pour tout

x\in I,~E(x)=\cdots

Or

\lim _{x\to +\infty }\cdots =\cdots

Donc

\lim _{x\to +\infty }E(x)=\cdots

On a les positions relatives :

${\begin{array}{c|ccc|}x&0&&+\infty \\\hline {\textrm {Signe~de}}~E(x)&&&\\\hline {\textrm {Position}}&&&\\\hline \end{array}}$

'Solution de l'exemple 2'

1. Déterminer le comportement de g en +∞

On factorise par les termes de plus haut degré et on simplifie :

Pour tout

x\in I,~g(x)={\frac {-2x^{2}+5x-3}{x-2}}={\frac {x^{2}\left(-2+{\frac {5}{x}}-{\frac {3}{x^{2}}}\right)}{x\left(1-{\frac {2}{x}}\right)}}=x\cdot {\frac {-2+{\frac {5}{x}}-{\frac {3}{x^{2}}}}{1-{\frac {2}{x}}}}

Or,

\lim _{x\to +\infty }-2+{\frac {5}{x}}-{\frac {3}{x^{2}}}=-2

et

\lim _{x\to +\infty }1-{\frac {2}{x}}=1

Donc $\lim _{x\to +\infty }f(x)=-\infty$

2. Trouver a et b tels que pour tout $x\in I,~g(x)=ax+b-{\frac {1}{x-2}}$

Soit $x\in I$ ${\begin{aligned}ax+b-{\frac {1}{x-2}}&={\frac {(ax+b)(x-2)}{x-2}}-{\frac {1}{x-2}}\\&={\frac {ax^{2}-2ax+bx-2b}{x-2}}-{\frac {1}{x-2}}\\&={\frac {ax^{2}+(b-2a)x-2b-1}{x-2}}\\\end{aligned}}$

On veut que, pour tout $x\in I,{\frac {-2x^{2}+5x-3}{x-2}}={\frac {ax^{2}+(b-2a)x-2b-1}{x-2}}$ , c'est-à-dire pour tout $x\in I,-2x^{2}+5x-3=ax^{2}+(b-2a)x-2b-1$

Deux fonctions polynomiales sont identiques en tout point si et seulement si leurs coefficients de même degré sont égaux. On aboutit alors au système suivant : ${\begin{cases}-2=a\\5=b-2a\\-3=-2b-1\end{cases}}$

Finalement ${\begin{cases}a=-2\\b=1\end{cases}}$

3. On pose pour tout $x\in I,~E(x)=g(x)-(ax+b)$ . Étudier le signe de E(x) et sa limite quand x tend vers plus l’infini.

Pour tout

x\in I,~E(x)=-{\frac {1}{x-2}}

Or

\lim _{x\to +\infty }x-2=+\infty

Donc

\lim _{x\to +\infty }E(x)=0

On en déduit que la droite ${\mathcal {D}}:y=-2x+1$ est asymptote à la courbe ${\mathcal {C}}_{g}$ de la fonction g.

L'étude du signe de E donne les positions relatives de ${\mathcal {C}}_{g}$ et ${\mathcal {D}}$ :

${\begin{array}{c|cccc|}x&3&&&+\infty \\\hline {\textrm {Signe~de}}~E(x)&&-&&\\\hline {\textrm {Position}}&&{\mathcal {C}}_{g}{\textrm {~en-dessous~de~}}{\mathcal {D}}&&\\\hline \end{array}}$

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.