Intégration en mathématiques/Exercices/Divers

Exercice 19-1

Pour $m$ et $n$ entiers naturels, on considère l'intégrale :

I(m,n)=\int _{a}^{b}(x-a)^{m}(b-x)^{n}\,\mathrm {d} x

.

1° Calculer $I(m,n)$ :

a) en utilisant le changement de variable

x-a=t

et la formule du binôme ;

b) en établissant, par intégration par parties, une relation de récurrence entre

I(m,n)

et

I(m+1,n-1)

, puis en déduisant

I(m,n)

du calcul de

I(m+n,0)

.

2° Déduire de ce qui précède que :

\sum _{i=0}^{n}{\frac {(-1)^{i}}{m+i+1}}{n \choose i}={\frac {1}{(m+n+1){m+n \choose n}}}

.

Solution

- $I(m,n)=\int _{0}^{b-a}t^{m}(b-a-t)^{n}\,\mathrm {d} t=\int _{0}^{b-a}t^{m}\sum _{i=0}^{n}{n \choose i}(b-a)^{n-i}(-t)^{i}\,\mathrm {d} t=(b-a)^{m+n+1}\sum _{i=0}^{n}{\frac {(-1)^{i}}{m+i+1}}{n \choose i}$ .
- Si $n>0$ , $I(m,n)={\frac {1}{m+1}}\underbrace {\left[(x-a)^{m+1}(b-x)^{n}\right]_{a}^{b}} _{0}+{\frac {n}{m+1}}\,I(m+1,n-1)$ .
  Or $I(m+n,0)={\frac {(b-a)^{m+n+1}}{m+n+1}}$ .
  Donc $I(m,n)={\frac {n}{m+1}}{\frac {n-1}{m+2}}\dots {\frac {1}{m+n}}\,I(m+n,0)={\frac {(b-a)^{m+n+1}}{(m+n+1){m+n \choose n}}}$ .
Immédiat.

Exercice 19-2

Soit :

I(a)=\int _{0}^{1}\left|x^{2}+a\right|\,\mathrm {d} x

.

Prouver que, pour tout $a$ :

I(a)\geqslant I\left(-{\frac {1}{4}}\right)

.

Solution

$\left(\int _{x^{2}>-a,\,0<x<1}-\int _{x^{2}<-a,\,0<x<1}\right)\left(x^{2}+a\right)\,\mathrm {d} x=$

$\left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}>-a,\,0<x<1}-\left[{\frac {x^{3}}{3}}+ax\right]_{x^{2}<-a,\,0<x<1}=$

${\begin{cases}{\text{si}}&a\leq -1&:&-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=-a-{\frac {1}{3}}\\{\text{si}}&-1\leq a\leq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{\sqrt {-a}}^{1}-\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{\sqrt {-a}}=a+{\frac {1}{3}}+{\frac {4(-a)^{3/2}}{3}}\\{\text{si}}&a\geq 0&:&\left[{\frac {x^{3}}{3}}+ax\right]_{0}^{1}=a+{\frac {1}{3}}\end{cases}}$

(dans chacun des deux cas $a=-1$ ou $a=0$ , communs à deux expressions, les deux fonctions de $a$ coïncident).

Cette fonction $I$ est décroissante sur $\left]-\infty ,-{\frac {1}{4}}\right]$ et croissante sur $\left[-{\frac {1}{4}},+\infty \right[$ .

Exercice 19-3

On considère, dans un repère orthonormal, la courbe $H$ d'équation :

y={\frac {1}{x}}

.

Soit $x$ un nombre strictement positif. On désigne par $M$ et $M'$ les deux points de la courbe $H$ d'abscisses respectives $x$ et ${\frac {\mathrm {e} ^{2}}{x}}$ , et $P$ et $P'$ leurs projetés orthogonaux sur l’axe des abscisses.

1° Calculer l’aire $S(x)$ de la surface limitée par l’axe des abscisses, les droites $(MP)$ et $(M'P')$ et la courbe $H$ .

2° On considère la fonction $S$ définie par :

{\begin{cases}S(x)=2-2\ln x,\quad {\text{pour }}0<x\leqslant \mathrm {e} \\S(x)=2\ln x-2,\quad {\text{pour }}x\geqslant \mathrm {e} .\end{cases}}

Calculer la dérivée de la fonction

S

pour

x\neq \mathrm {e}

Étudier la variation de

S

et construire son graphique.

Préciser les demi-tangentes à ce graphique au point d'abscisse

x=\mathrm {e}

.

3° Calculer les valeurs de $x$ pour lesquelles l'aire $S$ est égale à $2$ .

4° Étudier les limites à droite et à gauche en $\mathrm {e}$ de la fonction :

x\longmapsto {\frac {S(x)}{2(x-\mathrm {e} )}}

.

Solution

$S(x)=\left|\int _{x}^{\mathrm {e} ^{2}/x}{\frac {1}{t}}\,\mathrm {d} t\right|=\left|[\ln ]_{x}^{\mathrm {e} ^{2}/x}\right|=2\left|1-\ln x\right|$ .
$S'(x)=-{\frac {2}{x}}$ si $x<\mathrm {e}$ et $+{\frac {2}{x}}$ si $x>\mathrm {e}$ donc $S$ est décroissante sur $\left]0,\mathrm {e} \right]$ et croissante sur $\left[\mathrm {e} ,+\infty \right[$ . En $0$ et en $+\infty$ , elle tend vers $+\infty$ .
Le graphique de S est donné par ;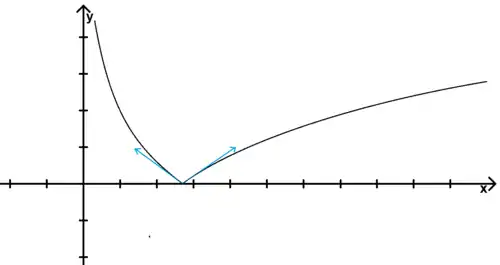

Les deux demi-tangentes au point $(\mathrm {e} ,0)$ ont pour équations $y=-{\frac {2x}{\mathrm {e} }}+2$ et $y=+{\frac {2x}{\mathrm {e} }}-2$ .
$S(x)=2\Leftrightarrow \left|1-\ln x\right|=1\Leftrightarrow x=1$ ou $\mathrm {e} ^{2}$ .
Quand $x\to \mathrm {e} ^{+}$ , ${\frac {S(x)}{2(x-\mathrm {e} )}}={\frac {\ln x-1}{x-\mathrm {e} }}\to \ln '(\mathrm {e} )={\frac {1}{\mathrm {e} }}$ et quand $x\to \mathrm {e} ^{-}$ , ${\frac {S(x)}{2(x-\mathrm {e} )}}\to -{\frac {1}{\mathrm {e} }}$ .

Exercice 19-4

On considère la fonction $f:\mathbb {R} \to \mathbb {R}$ définie par :

f(x)={\frac {\sin x}{\cos x+\sin x}}

.

1° Étudier son ensemble de définition, démontrer qu'elle est périodique de période $\pi$ et étudier sa variation dans l'intervalle $\left]-{\frac {\pi }{4}},\,{\frac {3\pi }{4}}\right[$ .

Tracer la courbe représentative de

f

dans un repère orthonormal.

2° Calculer les primitives de $f$ . On pourra mettre $f(x)$ sous la forme :

f(x)=A+B\left({\frac {-\sin x+\cos x}{\cos x+\sin x}}\right)

où

A

et

B

sont des constantes à préciser.

En déduire la valeur de l’aire du domaine compris entre la courbe, l'axe des abscisses et les deux droites d'équations

x=0

,

x={\frac {\pi }{2}}

.

Solution

$f$ est définie sur la réunion des intervalles $\left]-{\frac {\pi }{4}}+k\pi ,{\frac {3\pi }{4}}+k\pi \right[$ avec $k\in \mathbb {Z}$ et vérifie : $f(x+\pi )={\frac {-\sin x}{-\cos x-\sin x}}=f(x)$ .
$f'(x)={\frac {1}{(\cos x+\sin x)^{2}}}>0$ donc $f$ est strictement croissante sur chacun de ces intervalles. Ses limites à droite en $-{\frac {\pi }{4}}$ et à gauche en ${\frac {3\pi }{4}}$ sont respectivement $-\infty$ et $+\infty$ .
La courbe représentative de $f$ dans un repère orthonormal est :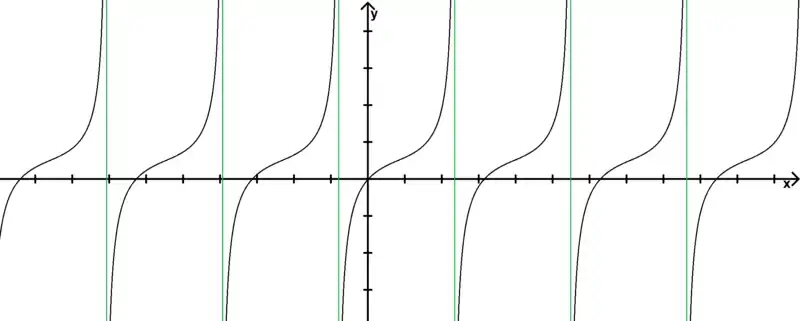

(Les asymptotes verticales sont représentées en vert).
- $f={\frac {1}{2}}-{\frac {1}{2}}\left({\frac {-\sin +\cos x}{\cos +\sin }}\right)$ a pour primitives $x\mapsto {\frac {x}{2}}-{\frac {1}{2}}\ln \left|\cos x+\sin x\right|+k$ avec $k\in \mathbb {R}$ .
- $\int _{0}^{\frac {\pi }{2}}f(x)\,\mathrm {d} x=\left[{\frac {x}{2}}-{\frac {1}{2}}\ln \left|\cos x+\sin x\right|\right]_{0}^{\frac {\pi }{2}}=\left[{\frac {x}{2}}\right]_{0}^{\frac {\pi }{2}}={\frac {\pi }{4}}$ .

Exercice 19-5

Soit la fonction $f:\mathbb {R} ^{*}\to \mathbb {R}$ définie par :

f(x)=\ln \left(x^{2}\right)

.

1° Étudier la variation de $f$ et la représenter graphiquement par rapport à un repère orthonormal $(0,\,{\vec {i}},\,{\vec {j}})$ . Soit $C$ , la courbe représentative.

2° Écrire l'équation de la tangente à $C$ au point $E$ ayant pour abscisse le nombre $\mathrm {e}$ .

3° Vérifier que la fonction $F$ définie par :

F(x)=x\ln \left(x^{2}\right)-2x

est une primitive de la fonction

f

dans chacun des intervalles où cette dernière est définie.

4° Évaluer l’aire du domaine plan délimité par l'axe des abscisses, la courbe $C$ et la tangente à $C$ au point $E$ .

Solution

$f$ est paire donc il suffit de l'étudier sur $\mathbb {R} _{+}^{*}$ . Sur cet intervalle, elle croît strictement de $-\infty$ à $+\infty$ . Elle s'annule en $1$ .
Le reste de l'étude se déduit par symétrie par rapport à l'axe des ordonnées et l'on obtient le tableau de variation :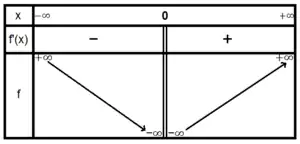

Le graphique C de la fonction f est alors :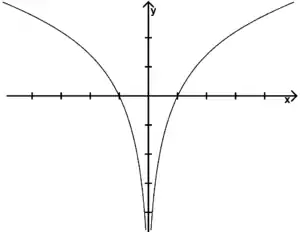
$f(\mathrm {e} )=2$ et $f'(\mathrm {e} )={\frac {2}{\mathrm {e} }}$ donc la tangente à $C$ au point $E$ a pour équation : $y={\frac {2}{\mathrm {e} }}(x-\mathrm {e} )+2$ , ou encore : $y={\frac {2x}{\mathrm {e} }}$ .
Graphique (réduire le zoom pour voir le point de tangence).
$F'=f$ .
$\mathrm {e} -\int _{1}^{\mathrm {e} }f(x)\,\mathrm {d} x=\mathrm {e} -\left[x\ln \left(x^{2}\right)-2x\right]_{1}^{\mathrm {e} }=\mathrm {e} -2$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.