Fonctions d'une variable complexe/Intégrales curvilignes

Chemins dans le plan complexe

Définitions

Un chemin est une application continue ${\displaystyle \gamma$ où [a,b] est un intervalle compact de $\mathbb {R}$ .

On appelle $\gamma (a)$ l'origine du chemin et $\gamma (b)$ la fin du chemin. Si $\gamma (a)=\gamma (b)$ le chemin est appelé chemin fermé ou encore lacet.

Si $\gamma$ est $C^{1}([a,b])$ alors le chemin est dit continûment dérivable.

Enfin, si $\gamma$ est $C^{1}(I_{k})$ où $[a,b]=\bigcup _{k=1}^{n}I_{k}\;\;\;k,n\in \mathbb {N}$ alors le chemin est dit continûment dérivable par morceaux.

Exemple

Le cercle de rayon $R$ et de centre $z_{0}$ est l'image du chemin $\gamma (t)=Re^{it}+z_{0},\;t\in [0,2\pi ]$

On peut toujours se ramener à des chemins définis sur l'intervalle $[0,1]$ via un changement de variable affine. Ainsi, $\gamma (t)$ défini pour $t\in [a,b]$ se ramène à $\gamma _{0}:[0,1]\rightarrow \mathbb {C}$ , avec $\gamma _{0}(u)=\gamma ((b-a)u+a)$ .

On confondra souvent dans le langage informel un chemin et son image.

Chemins homotopes

Soient $\gamma$ et $\Gamma$ deux chemins tels que :

${\displaystyle \gamma ,\;\Gamma$

On introduit alors la notion suivante :

Chemins homotopes à extrémités fixes

Les chemins $\gamma$ et $\Gamma$ sont dits homotopes dans $\Omega$ comme chemins à extrémités fixes lorsqu’il existe une application continue

$H:[a,b]\times [0,1]\rightarrow \Omega \subset \mathbb {C}$

telle que :

$\forall t\in [a,b],\quad \gamma (t)=H(t,0)\;$
$\forall t\in [a,b],\quad \Gamma (t)=H(t,1)\;$
$\forall s\in [0,1],\quad H(a,s)=\gamma (a)=\Gamma (a)\;$
$\forall s\in [0,1],\quad H(b,s)=\gamma (b)=\Gamma (b)\;$

Cette définition signifie que deux chemins possédant les mêmes extrémités sont homotopes si l'un peut se déformer continûment sur l'autre. En particulier, l'image de $H$ dans $\mathbb {C}$ ne contient pas de "trou topologique".

Chemins fermés homotopes

Les chemins $\gamma$ et $\Gamma$ sont dits homotopes dans $\Omega$ comme chemins fermés lorsqu’il existe une application continue

$H:[a,b]\times [0,1]\rightarrow \Omega \subset \mathbb {C}$

telle que :

$\forall t\in [a,b],\quad \gamma (t)=H(t,0)\;$
$\forall t\in [a,b],\quad \Gamma (t)=H(t,1)\;$
$\forall s\in [0,1],\quad H(a,s)=H(b,s)\;$

Connexité simple

Ouvert simplement connexe

Un ouvert (ensemble) $\Omega \subset \mathbb {C}$ est dit simplement connexe (ensemble) si tout chemin fermé contenu dans cet ouvert est homotope à un point (i.e. un chemin constant), ou de façon équivalente, si tout lacet est homotope à un point.

Concrètement, lorsqu'un ensemble est "troué", on ne peut contracter les lacets qui font le tour d'un de ces trous, c’est le cas pour un anneau ou un disque épointé, par exemple. La simple connexité dans le plan est la propriété des ensembles qui n'ont pas de trou.

Proposition

Les (ouverts) convexes et, plus généralement, les ouverts (ensembles) étoilés sont simplement connexes.

Quelques ouverts simplement connexes

Le plan complexe $\mathbb {C}$ ,
La boule (appelée aussi disque) ouverte de rayon R centrée en $z_{0}$ : $\mathrm {B} =\left\{z\in \mathbb {C$ ,
Le domaine $\Omega =\mathbb {C} \backslash ]-\infty ,0]$ de définition de $Log$ .

Intégrale curviligne

Définition de l'intégrale curviligne

Soit $f:\Omega \subset \mathbb {C} \rightarrow \mathbb {C}$ et un chemin continûment dérivable sur $[a,b]\subset \mathbb {R}$ tel que ${\displaystyle \gamma$ .

On définit l'intégrale curviligne de ƒ le long de $\gamma$ par : $\int _{\gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}f(\gamma (t))\mathrm {\gamma } \,'\left(t\right)\,\mathrm {d} t$ .

Si $\gamma$ est un chemin fermé on utilise parfois la notation (surtout dans les anciens ouvrages et les ouvrages de physique) : $\oint _{\gamma }f(z)\,\mathrm {d} z$ .

Notation alternative pour l'intégrale curviligne et lien avec l'analyse vectorielle

On a aussi $\gamma (t)=\gamma _{1}(t)+i\gamma _{2}(t)\;$ où $\gamma (t)_{1}$ et $\gamma _{2}$ désignent respectivement les parties réelles et imaginaires de $\gamma$ . On peut alors définir ${\vec {\gamma (t)}}=(\gamma _{1}(t),\gamma _{2}(t))$

$\int _{\gamma }f(z)\,\mathrm {d} z=\int _{\vec {\gamma }}f\,\mathrm {d} x+if\mathrm {d} y$ (intégration par rapport à la partie réelle et imaginaire) ce qui montre le lien entre l'intégrale curviligne dans $\mathbb {C}$ et l'intégrale curviligne de fonctions vectorielles. Puisque toute fonction $f:\mathbb {C} \rightarrow \mathbb {C}$ est équivalente à une fonction vectorielle $f:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}$

Inégalité ML

Lemme d'estimation (standard)

Si $f:\Omega \subset \mathbb {C} \rightarrow \mathbb {C}$ telle que $|f|$ est bornée sur un chemin $\gamma$ rectifiable et continûment dérivable de longueur $L(\gamma )$ , alors il existe $M\in \mathbb {R}$ tel que l’on a l'inégalité: $|\int _{\gamma }f(z)\mathrm {dz} |\leq ML(\gamma )$
Avec en particulier $M=\mathrm {sup_{\gamma }} |f(z)|$

Cette inégalité est très utile pour l'évaluation des intégrales curvilignes, en particulier pour montrer que certaines intégrales curvilignes sont nulles.

Théorème de Cauchy (invariance des intégrales curvilignes par homotopie)

Théorème de Cauchy

Soit $f:\Omega \subset \mathbb {C} \rightarrow \mathbb {C}$ holomorphe et $\gamma$ et $\Gamma$ deux chemins homotopes continûment dérivables sur $[a,b]\subset \mathbb {R}$ tels que ${\displaystyle \gamma ,\Gamma$ .

On alors: $\int _{\gamma }f(z)\,\mathrm {d} z=\int _{\Gamma }f(z)\,\mathrm {d} z$

Indice d'un lacet

L'indice d'un lacet $\gamma$ par rapport à un point $z_{0}\in \mathbb {C}$ , noté $Ind(\gamma ,z_{0})$ est "le nombre de tours" que fait le lacet autour de ce point. Ce nombre est positif pour les tours dans le sens trigonométrique (direct, anti-horlogique) et négatif dans le sens inverse (indirect, horlogique).

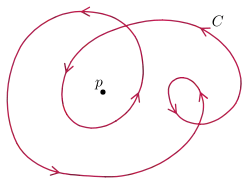
Ce lacet a un indice égal à deux autour de p (Ind(C,p)=2).

indice d'un lacet autour d'un point

L'indice d'un lacet $\gamma$ par rapport à un point $z_{0}\in \mathbb {C}$ est défini par:
$\mathrm {Ind(\gamma ,z_{0})$

Primitive des fonctions holomorphes

Définition

Soit $\Omega$ un ouvert de $\mathbb {C}$ et $f,\,F$ des fonctions définies sur $\Omega$ . $F$ est appelée primitive de $f$ si elle est holomorphe sur $\Omega$ et qu'elle vérifie $F\,'=f$ .

Proposition

Lorsque $\Omega$ est connexe, deux primitives d'une même fonction diffèrent d'une constante.

Propriété

Si $f$ est une fonction holomorphe définie sur un ouvert simplement connexe $\Omega$ de $\mathbb {C}$ , alors il existe une fonction $F$ holomorphe sur $\Omega$ telle que $F\,'=f$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.